7.5: Full Hypothesis Test Examples
- Page ID
- 79055
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Tests on Means
Example \(\PageIndex{1}\)
Jeffrey, as an eight-year old, established a mean time of 16.43 seconds for swimming the 25-yard freestyle.
His dad, Frank, thought that Jeffrey could swim the 25-yard freestyle faster using goggles. Frank bought Jeffrey a new pair of expensive goggles and timed Jeffrey for 15 25-yard freestyle swims. For the 15 swims, Jeffrey's mean time was 16 seconds, with a standard deviation of 0.8 seconds. Frank thought that the goggles helped Jeffrey to swim faster than the 16.43 seconds. Conduct a hypothesis test using test statistics and \(p\)-values with a preset \(\alpha = 0.05\).
- Answer
-
Set up the Hypothesis Test:
Since the problem is about a mean, this is a test of a single population mean.
Set the null and alternative hypothesis:
In this case there is an implied challenge or claim. This is that the goggles will reduce the swimming time. The effect of this is to set the hypothesis as a one-tailed test. The claim will always be in the alternative hypothesis because the burden of proof always lies with the alternative. Remember that the status quo must be defeated with a high degree of confidence, in this case 95% confidence. The null and alternative hypotheses are thus:
\(H_0: \mu \geq 16.43\) \(H_a: \mu < 16.43\)
For Jeffrey to swim faster, his time should be less than 16.43 seconds. The "<" tells you this is left-tailed.
Determine the distribution needed:
Random variable: \(\overline x\) = the mean time to swim the 25-yard freestyle.
Distribution for the test statistic:
The sample size is less than 30 and we do not know the population standard deviation so this is a t-test. The proper formula is: \(t_{obs}=\frac{\overline{x}-\mu_{0}}{s / \sqrt{n}}\)
\(\mu_ 0 = 16.43\) comes from \(H_0\) and not the data. \(\overline x = 16\), \(s = 0.8\), and \(n = 15\).
Our step 2, setting the level of confidence, has already been determined by the problem, \(\alpha\) of .05 corresponds to a 95% confidence level. It is worth thinking about the meaning of this choice. The Type I error is to conclude that Jeffrey swims the 25-yard freestyle, on average, in less than 16.43 seconds when, in fact, he actually swims the 25-yard freestyle, on average, in 16.43 seconds or more. (Reject the null hypothesis when the null hypothesis is true.) For this case the only concern with a Type I error would seem to be that Jeffrey’s dad may fail to bet on his son’s victory because he does not have appropriate confidence in the effect of the goggles.
To find the critical value we need to select the appropriate test statistic. We have concluded that this is a t-test on the basis of the sample size and that we are interested in a population mean. We can now draw the graph of the t-distribution and mark the critical value. For this problem the degrees of freedom are n-1, or 14. Looking up 14 degrees of freedom at the 0.05 column of the t-table we find 1.761. This is the critical value and we can put this on our graph.
Step 3 is the calculation of the test statistic using the formula we have selected. We find that the observed test statistic is -2.08, meaning that the sample mean is 2.08 standard errors below the hypothesized mean of 16.43.
\[t_{obs}=\frac{\overline{x}-\mu_{0}}{s / \sqrt{n}}=\frac{16-16.43}{.8 / \sqrt{15}}=-2.08\nonumber\]
Figure \(\PageIndex{1}\)
Step 4 has us compare the test statistic and the critical value and mark these on the graph. We see that the test statistic is in the tail and thus we move to step 4 and reach a conclusion. The probability that an average time of 16 minutes could come from a distribution with a population mean of 16.43 minutes is too unlikely to have occurred under the null hypothesis. We reject the null.
Step 5 has us state our conclusions first formally and then less formally. A formal conclusion would be stated as: “With a 95% level of confidence we reject the null hypothesis that the swimming time with goggles comes from a distribution with a population mean time of 16.43 minutes.” Less formally, “With 95% confidence, we believe that the goggles improved swimming speed".
If we wished to use the \(p\)-value system of reaching a conclusion we would calculate the statistic and take the additional step to find the probability of being 2.08 standard errors from the mean on a t-distribution. The \(p\)-value interval is (.025, .05), that we get by looking up the one-tailed probabilities associated with the closest t-scores (1.761 and 2.145) to the observed test statistic (-2.08) in the relevant df row of 14 in the t-table. Comparing this interval to the significance level of .05 we see that we reject the null. The \(p\)-value has been put on the graph as the shaded area beyond -2.08 and it shows that it is smaller than the hatched area which is the \(\alpha\) level of 0.05. Both methods reach the same conclusion that we reject the null hypothesis.
Exercise \(\PageIndex{1}\)
The mean throwing distance of a football for Marco, a high school freshman quarterback, is 40 yards, with a standard deviation of two yards. The team coach tells Marco to adjust his grip to get more distance. The coach records the distances for 20 throws. For the 20 throws, Marco’s mean distance was 45 yards. The coach thought the different grip helped Marco throw farther than 40 yards. Conduct a hypothesis test using a preset \(\alpha = 0.05\). Assume the throw distances for footballs are normal.
First, determine what type of test this is, set up the hypothesis test, find the \(p\)-value, sketch the graph, and state your conclusion.
Example \(\PageIndex{2}\)
Jane has just begun her new job as on the sales force of a very competitive company. In a sample of 16 sales calls it was found that she closed the contract for an average value of 108 dollars with a standard deviation of 12 dollars. Company policy requires that new members of the sales force must exceed an average of $100 per contract during the trial employment period. Can we conclude that Jane has met this requirement at the significance level of 5%?
- Answer
-
- \(H_0: \mu \leq 100\)
\(H_a: \mu > 100\)
The null and alternative hypothesis are for the parameter \(\mu\) because the number of dollars of the contracts is a continuous random variable. Also, this is a one-tailed test because the company has only an interested if the number of dollars per contact is below a particular number not "too high" a number. This can be thought of as making a claim that the requirement is being met and thus the claim is in the alternative hypothesis. - Test statistic: \(t_{obs}=\frac{\overline{x}-\mu_{0}}{\frac{s}{\sqrt{n}}}=\frac{108-100}{\left(\frac{12}{\sqrt{16}}\right)}=2.67\)
- Critical value: \(t_\alpha=1.753\) with \(n-1\) degrees of freedom = 15
The test statistic is a Student's t because the sample size is below 100; therefore, we cannot use the normal distribution. Comparing the observed value of the test statistic and the critical value of t at a 5% significance level, we see that the observed value is in the tail of the distribution. Thus, we conclude that 108 dollars per contract is significantly larger than the hypothesized value of 100 and thus we must reject the null hypothesis. There is evidence that Jane's performance meets company standards.
Figure \(\PageIndex{2}\)
- \(H_0: \mu \leq 100\)
Exercise \(\PageIndex{2}\)
It is believed that a stock price for a particular company will grow at a rate of $5 per week with a standard deviation of $1. An investor believes the stock won’t grow as quickly. The changes in stock price is recorded for ten weeks and are as follows: $4, $3, $2, $3, $1, $7, $2, $1, $1, $2. Perform a hypothesis test using a 5% level of significance. State the null and alternative hypotheses, state your conclusion, and identify the Type I and Type II errors.
Example \(\PageIndex{3}\)
A manufacturer of salad dressings uses machines to dispense liquid ingredients into bottles that move along a filling line. The machine that dispenses salad dressings is working properly when 8 ounces are dispensed. Suppose that the average amount dispensed in a particular sample of 35 bottles is 7.91 ounces with a variance of 0.03 ounces squared, \(s^2\). Is there evidence that the machine should be stopped and production wait for repairs? The lost production from a shutdown is potentially so great that management feels that the level of confidence in the analysis should be 99%.
Again we will follow the steps in our analysis of this problem.
- Answer
-
STEP 1: Set the null and alternative hypothesis.
The random variable is the quantity of fluid placed in the bottles. This is a continuous random variable and the parameter we are interested in is the mean. Our hypothesis therefore is about the mean. In this case we are concerned that the machine is not filling properly. From what we are told it does not matter if the machine is over-filling or under-filling, both seem to be an equally bad error. This tells us that this is a two-tailed test: if the machine is malfunctioning it will be shutdown regardless if it is from over-filling or under-filling. The null and alternative hypotheses are thus:
\[H_0:\mu=8\nonumber\]
\[Ha:\mu \neq 8\nonumber\]
STEP 2: Decide the level of significance and draw the graph showing the critical value.
This problem has already set the level of confidence at 99%. The decision seems an appropriate one and shows the thought process when setting the significance level. Management wants to be very certain, as certain as probability will allow, that they are not shutting down a machine that is not in need of repair. To draw the distribution and the critical value, we need to know which distribution to use. Because the sample size is under 100, the appropriate distribution is the t-distribution and the relevant critical value is 2.750 from the t-table at 0.005 column and 30 degrees of freedom (closest available row to our actual 34 df here). We need to draw the graph and mark these points.
STEP 3: Calculate sample parameters and the test statistic.
The sample parameters are provided, the sample mean is 7.91 and the sample variance is .03 and the sample size is 35. We need to note that the sample variance was provided, not the sample standard deviation, which is what we need for the formula. Remembering that the standard deviation is simply the square root of the variance, we therefore know the sample standard deviation, \(s\), is 0.173. With this information we can calculate the test statistic as -3.07, and mark it on the graph.
\[t_{obs}=\frac{\overline{x}-\mu_{0}}{s / \sqrt{n}}=\frac{7.91-8}{\cdot 173 / \sqrt{35}}=-3.07\nonumber\]
STEP 4: Compare test statistic and the critical values.
Now we compare the test statistic and the critical value by placing the test statistic on the graph. The test statistic is in the tail, decidedly greater than the critical value of 2.750. We note that even the very small difference between the hypothesized value and the sample value is still a large number of standard errors. The sample mean is only 0.08 ounces different from the required level of 8 ounces, but it is 3+ standard errors away from the required 8 ounces, and thus we reject the null hypothesis.
STEP 5: Reach a conclusion.
Three standard errors of a test statistic will guarantee that the test will fail. The probability that anything is beyond three standard errors of a hypothesized null value - given a large enough sample size - is close to zero. Looking at the closest t-scores in df=30 row in the t-table, we get the \(p\)-value interval of (.01, .002) after doubling the one-tailed probabilities of .005 and .001. Our formal conclusion would be “At a 99% level of confidence, we reject the null hypothesis that the sample mean came from a distribution with a mean of 8 ounces”. Or less formally, and getting to the point, “At a 99% level of confidence, we conclude that the machine is under-filling the bottles and is in need of repair”.
Hypothesis Test for Proportions
Just as there were confidence intervals for proportions, or more formally, the population parameter \(P\), there is the ability to test hypotheses concerning \(P\).
The estimated value (point estimate) for \(P\) is \(P^{\prime}\) where \(P^{\prime} = x/n\), \(x\) is the number of observations in the category of interest in the sample and \(n\) is the sample size.
When you perform a hypothesis test of a population proportion \(P\), you take a random sample from the population. To ensure normality of the distribution, sampling must be random and the total sample size must be greater than 100. There is no distribution that can correct for this small sample bias and thus if these conditions are not met we simply cannot test the hypothesis with the data available at that time. We met this condition when we were first estimating confidence intervals for \(P\).
Again, we begin with the modified standardizing formula:
\[z=\frac{P^{\prime}-P}{\sqrt{\frac{P(1-P)}{n}}}\nonumber\]
Substituting \(P_0\), the hypothesized value of \(P\), we have:
\[z_{obs}=\frac{P^{\prime}-P_{0}}{\sqrt{\frac{P_{0} (1-P_{0})}{n}}}\nonumber\]
This is the test statistic for testing hypothesized values of \(P\), where the null and alternative hypotheses take one of the following forms:
| Two-tailed test | One-tailed test | One-tailed test |
|---|---|---|
| \(H_0: P = P_0\) | \(H_0: P \leq P_0\) | \(H_0: P \geq P_0\) |
| \(H_a: P \neq P_0\) | \(H_a: P > P_0\) | \(H_a: P < P_0\) |
Table \(\PageIndex{1}\)
The decision rule stated above applies here also: if the calculated value of \(z_{obs}\) shows that the sample proportion is "too many" standard errors from the hypothesized proportion, the null hypothesis is rejected. The decision as to what is "too many" is pre-determined by the analyst depending on the level of significance required in the test.
Example \(\PageIndex{4}\)
The mortgage department of a large bank is interested in the nature of loans of first-time borrowers. This information will be used to tailor their marketing strategy. They believe that 50% of first-time borrowers take out smaller loans than other borrowers. They perform a hypothesis test to determine if the percentage is different from 50%. They sample 101 first-time borrowers and find 54 of these loans are smaller that the other borrowers. For the hypothesis test, they choose a 5% level of significance.
- Answer
-
STEP 1: Set the null and alternative hypothesis.
\(H_0: P = 0.50\) \(H_a: P \neq 0.50\)
The words "is different from" tell you this is a two-tailed test. The Type I and Type II errors are as follows: The Type I error is to conclude that the proportion of borrowers is different from 50% when, in fact, the proportion is actually 50%. (Reject the null hypothesis when the null hypothesis is true). The Type II error is there is not enough evidence to conclude that the proportion of first time borrowers differs from 50% when, in fact, the proportion does differ from 50%. (You fail to reject the null hypothesis when the null hypothesis is false.)
STEP 2: Decide the level of significance and draw the graph showing the critical value
The level of confidence has been set by the problem at 95%. Because this is two-tailed test one-half of the \(\alpha\) value will be in the upper tail and one-half in the lower tail as shown on the graph. The critical value for the normal distribution at the 95% level of confidence is 1.96. This can easily be found on the Student’s t-table at the very bottom at infinite degrees of freedom remembering that at infinity the t-distribution is the normal distribution. Of course, the value can also be found on the standard normal table but you have go looking for the tail probability, \(\alpha\)/2, inside the body of the table and then read out to the sides and top for the number of standard errors.
Figure \(\PageIndex{3}\)
STEP 3: Calculate the sample parameters and critical value of the test statistic.
The test statistic is a normal distribution, \(z\), for testing proportions and is:
\[z=\frac{P^{\prime}-P_{0}}{\sqrt{\frac{P_{0} (1-P_{0})}{n}}}=\frac{.53-.50}{\sqrt{\frac{.5(.5)}{101}}}=0.60\nonumber\]
For this case, the sample of 101 found 54 first-time borrowers were different from other borrowers. The sample proportion, \(P^{\prime} = 54/101= 0.53\) The test question, therefore, is : “Is 0.53 significantly different from 0.50?” Putting these values into the formula for the test statistic we find that 0.53 is only 0.60 standard errors away from 0.50. This is barely off of the mean of the standard normal distribution of zero. There is virtually no difference from the sample proportion and the hypothesized proportion in terms of standard errors.
STEP 4: Compare the test statistic and the critical value.
The observed value is well within the critical values of \(\pm 1.96\) standard errors and thus we cannot reject the null hypothesis. To reject the null hypothesis we need significant evidence of difference between the hypothesized value and the sample value. In this case the sample value is very nearly the same as the hypothesized value measured in terms of standard errors.
STEP 5: Reach a conclusion.
The formal conclusion would be “At a 95% level of confidence we cannot reject the null hypothesis that 50% of first-time borrowers have the same size loans as other borrowers”. Less formally, we would say that “There is no evidence that one-half of first-time borrowers are significantly different in loan size from other borrowers”. Notice the length to which the conclusion goes to include all of the conditions that are attached to the conclusion. Statisticians, for all the criticism they receive, are careful to be very specific even when this seems trivial. Statisticians cannot say more than they know and the data constrain the conclusion to be within the metes and bounds of the data.
Exercise \(\PageIndex{3}\)
A teacher believes that 85% of students in the class will want to go on a field trip to the local zoo. She performs a hypothesis test to determine if the percentage is the same or different from 85%. The teacher samples 104 students and 89 reply that they would want to go to the zoo. For the hypothesis test, use a 1% level of significance.
Example \(\PageIndex{5}\)
Suppose a consumer group suspects that the proportion of households that have three or more cell phones is 30%. A cell phone company has reason to believe that the proportion is not 30%. Before they start a big advertising campaign, they conduct a hypothesis test using 90% confidence. Their marketing people survey 150 households with the result that 43 of the households have three or more cell phones.
- Answer
-
Here is an abbreviated version of the system to solve hypothesis tests applied to a test on a proportions.
\[H_0 : P = 0.3 \nonumber\]
\[H_a : P \neq 0.3 \nonumber\]
\[n = 150\nonumber\]
\[P^{\prime}=\frac{x}{n}=\frac{43}{150}=0.287\nonumber\]
\[z_{obs}=\frac{P^{\prime}-P_{0}}{\sqrt{\frac{P_{0} (1-P_{0})}{n}}}=\frac{0.287-0.3}{\sqrt{\frac{.3(.7)}{150}}}=0.347\nonumber\]
At a confidence level of 90% we cannot reject the null hypothesis that the consumer group is correct.
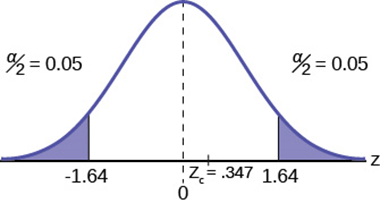
Figure \(\PageIndex{4}\)
Example \(\PageIndex{6}\)
In a study of 420,019 cell phone users, 172 of the subjects developed brain cancer. Test the claim that cell phone users developed brain cancer at a greater rate than that for non-cell phone users (the rate of brain cancer for non-cell phone users is 0.0340%). Since this is a critical issue, use a 0.005 significance level. Explain why the significance level should be so low in terms of a Type I error.
- Answer
-
We need to conduct a hypothesis test on the claimed cancer rate. Our hypotheses will be:
\(H_0: P \leq 0.00034\) \(H_a: P > 0.00034\)If we commit a Type I error, we are essentially accepting an incorrect claim. Since the claim describes cancer-causing environments, we want to minimize the chances of incorrectly identifying causes of cancer.

