Addendum B: Internal Rate of Return and Net Present Value
- Page ID
- 86743
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)“Net Present Value?! I barely understand what the baffling terms Internal Rate of Return and Present Value mean. Now you want to confuse me more? What is Net Present Value?!” Relax. Again, the words are more bewildering than the actual concept and its usage. In this addendum, we are going to give you an idea of what you will see if you ever take an upper-division or graduate level finance class at the university. You know those types of classes? They are similar to taking a swimming class where they teach you all about swimming but you never jump in the water or a driver’s education class where you learn all about cars but never get behind the wheel and venture out onto the roads. We will also see how the Internal Rate of Return is calculated by the computer and understand why we don’t ever want to have to do it manually more than once in our lives.
Recall the fundamental assertion in finance that the value of an investment is based upon the Present Value of its future cash flows. In our class, we learned how to compute the Present Value of the future stream of cash flows from stocks and bonds. We started with the dividends and the predicted future stock prices from stocks. We then used interest payments and principal repayments from bonds. However, calculating the Present Value of future cash flows is not limited to just stocks and bonds. Do you remember the original formula for the Dividend Discount Models?
We can use this formula to calculate the Present Value of any stream of cash flows from any source. The investment could be a real estate venture, or a factory, a bridge, or water project. It could even be a nuclear reactor. We can use the model for any vehicle that will produce income in the future. We saw that calculating the Present Value manually can be tedious and unwieldy. Luckily, we have electronic spreadsheets to do the job for us quickly. The spreadsheets also allow us to change our parameters and assumptions and instantly show us the new results. Very cool!
Let’s revisit our Pretzels Unlimited example. We said that Pretzels Unlimited was selling for $22 per share and that we believed they would pay us $2.00 per share in dividends in 2025 and then increase their dividends to $2.20 in 2026, $2.30 in 2027, and $2.30 in 2028. We expected the price to be $27 per share at the end of 2028. Our required rate of return is 12%. We put the years in the first column and the future cash flows in the second column.
| Year | Future Cash Flows | Present Value Multipliers12% | Discounted Cash Flows |
| 2025 | $2.00 | 0.893 | $1.786 |
| 2026 | $2.20 | 0.797 | $1.7534 |
| 2027 | $2.30 | 0.712 | $1.6376 |
| 2028 | $2.30 + $27 = $29.30 | 0.636 | $18.6348 |
| Total: | ≅ $23.81 | ||
We manually found the Present Value multipliers for years 1 through 4 at 12% in the present value table. We then multiplied the future cash flows by the Present Value multipliers to compute the Present Values, also called the Discounted Cash Flows, in the last column. Last, we summed the Discounted Cash Flows in the last column to compute the Present Value for the stock. The model says that we believe that Pretzels Unlimited is worth $23.81 if we require a 12% rate of return. With a market price of only $22, the model says that this stock is possibly an attractive investment for us. (Hopefully, you were able to follow along easily. If not, contact me now! You can’t leave our class without understanding and being able to use this model. It is bad for my self-esteem! Plus, what will people say when you tell them you didn’t learn how to discount a future stream of income in our Introduction to Investments class? Perish the thought!)
The Present Value tells us what we believe the future stream of income is worth today given our required rate of return. The current market price is what we have to pay for that future stream of income. If the Present Value is roughly equal to or greater than the current market price, then we predict that it is a potentially good investment and something we should investigate further. If the Present Value is below the market price, then we should either decide to look for a better investment elsewhere or maybe lower our expected return from this particular investment. Recall that the required rate of return is very important because as we change the required rate of return, the Present Value changes, sometimes greatly.
Okay, so what is Net Present Value? Net Present Value, often abbreviated NPV, takes into account all cash flows, both positive and negative. Cash inflows are what we call the money that we receive from an investment. Cash outflows are payments that we have to make to purchase or maintain an investment. If the Net Present Value is positive, then it may be a potentially good investment for us. Contrariwise, if the Net Present Value is negative, then it may not be a potentially good investment for our required rate of return. Net Present Value is much more popular when you get to upper division and graduate level finance classes at the university.
To calculate the Net Present Value for Pretzels Unlimited, we need to add a row for the initial $22 purchase of the stock. The present value multiplier is 1.000 because we are buying the stock now, in the present.
| Year | All Cash Flows, Negative and Positive | Present Value Multipliers12% | Discounted Cash Flows |
| ($22.00) | 1.000 | ($22.00) | |
| 2025 | $2.00 | 0.893 | $1.786 |
| 2026 | $2.20 | 0.797 | $1.7534 |
| 2027 | $2.30 | 0.712 | $1.6376 |
| 2028 | $2.30 + $27 = $29.30 | 0.636 | $18.6348 |
| Total: | ≅ $1.81 | ||
The Net Present Value is positive because the Present Value of the future cash flows is greater than the market price, our initial cash outflow. When a project has a positive Net Present Value, the model is telling us that we have a potentially good investment for our required rate of return. If the Net Present Value is negative, then the model is suggesting that we might not get the rate of return that we desire. We might decide to lower our required rate of return or discontinue our research into this particular investment. Either way, as we have emphasized repeatedly, this calculation is not the end of our research. It is only the beginning.
Are you sick and tired of calculating the Present Value using the Present Value tables? Good! That means you know how to calculate Present Value and understand what it means to discount a stream of future cash flows and I have done my job. (Hey! It is easier than using the formula with the exponents, right?) But you also know how to use an even easier way! Spreadsheets calculate Present Value for us without breaking a sweat
This brings us back to Internal Rate of Return, the very popular measure that business people and investors use when measuring the rate of return from a stream of future income. As mentioned, you will learn how to compute the Internal Rate of Return manually if you go on to an upper division or graduate level finance class at the university. Specifically, the Internal Rate of Return is the rate of return where the Net Present Value equals zero. “Huh? What?” Let’s see if using a spreadsheet can help us understand this concept more easily.
Let’s translate the table above into an electronic spreadsheet:

In this spreadsheet, we enter the Required Rate of Return at the top and then the expected future cash flows, both positive and negative in the second column. The spreadsheet does all the rest of the calculations and gives us a Net Present Value of $1.80. (The result is a penny off from our previous result because the spreadsheet is using 20 digits of accuracy for the present value multipliers where we only used 3 digits of accuracy from the present value table.)
Again, because the Net Present Value is positive, the model is saying that our investment is a potentially good one for us if we require a rate of return of 12%. But what if we required a rate of return of 16%? Let’s see what the new Net Present Value would be.

With a required rate of return of 16%, the Net Present Value has swung from a positive $1.80 to a negative 99¢. The model is telling us, given the expected future cash flows, we won’t receive a rate of return of 16%. But do you also see what else happened? The Net Present Value is now closer to zero. Recall that we stated that the Internal Rate of Return is the rate of return where the Net Present Value equals zero. By choosing different required rates of return, we can converge upon the required rate of return where the Net Present Value is equal to zero. Let’s try 14%.

Aha! We have swung back to a positive Net Present Value and this time our result is even closer to zero. We are now only 35¢ away from zero. We are converging upon the required rate of return where the Net Present Value will be equal to zero. When we finally hit that point, we will have found the Internal Rate of Return.
And now you understand why we don’t ever want to have to calculate the Internal Rate of Return manually. We have to iteratively compute Net Present Values until we reach the required rate of return where the Net Present Value is zero. That is why we have computers. We let the computer do the grunt work. All we do is enter the Required Rate of Return and the future cash flows.
Another way of computing Internal Rate of Return is to create a graph from a table of Net Present Values.
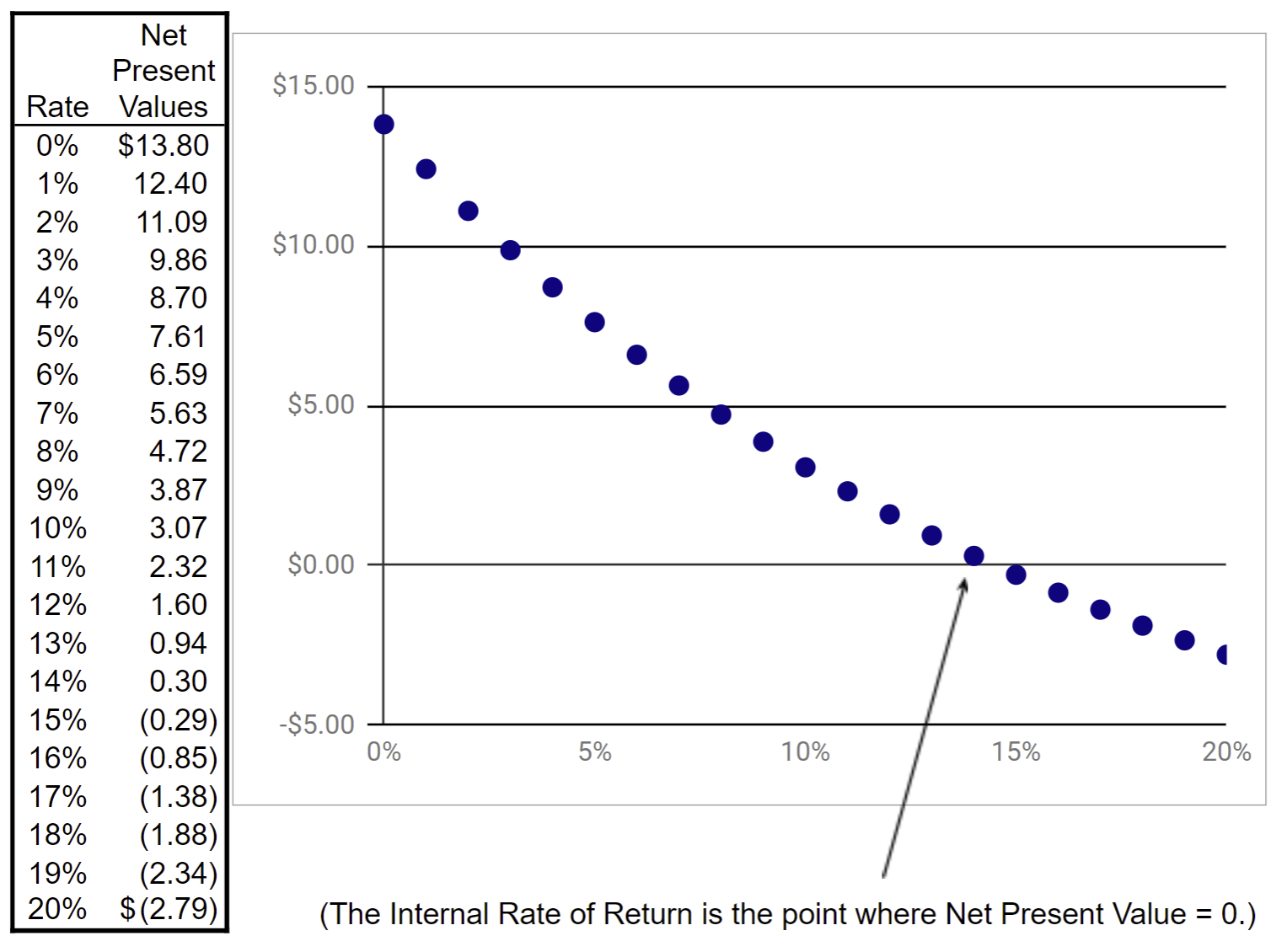
On the left, we have constructed a table of the Net Present Values for required rates of return from 0% to 20%. We then graphed the table on the right. Do you see where the Net Present Value is equal to zero? It appears to be at approximately 14.5%. Let’s use the Internal Rate of Return spreadsheet function, =IRR, to calculate the Internal Rate of Return precisely.

The spreadsheet took our cash flows, both positive and negative, and our guess of a 12% Internal Rate of Return, and then did all the busy work to produce an Internal Rate of Return of 14.51%. Aren’t you glad we have spreadsheets? I sure am!
Let’s turn our attention to bonds. The following spreadsheet is showing the Internal Rate of Return for a 10-year, 8% bond selling for $1,200.

The Internal Rate of Return is 5.36%. The approximation formula that we learned in chapter 9 returns 5.45%. Pretty close, huh? But the curious feature about this spreadsheet is that no matter how we play with the parameters of the bond, the Net Present Value will always be zero. Why is that? Recall that the Internal Rate of Return is the rate of return where the Net Present Value is zero. If we use the Internal Rate of Return to compute the Net Present Value as we did here, by definition, we are going to receive zero. This is yet another confirmation that bonds are indeed boring.
Now, let’s take a look at a real estate investment.

The price of real estate in the San Diego area is insane. As of May 2025, one can find a small duplex in the suburban city of Chula Vista, just south of San Diego, for approximately $800,000. Let’s assume that the two two-bedroom units will produce $2,000 each after expenses and that rents will increase at an annual rate of 5%. Although difficult to believe, this has been the reality, especially recently. Let’s also assume that we are paying cash for the duplex. For our expected price of the property in 30 years, let’s throw a number into the air and say that we believe it will be worth $2,000,000. If we required a 10% rate of return, the spreadsheet tells us that the Net Present Value will be over $33,000 and the investment will produce an Internal Rate of Return of $10.34%.
Do you see any problems with our assumptions? First, is it reasonable to assume that rents will increase 5% yearly for 30 years? Is it believable that a duplex house will be worth $2,000,000 in 30 years? These are dubious predictions at best. However, the most glaring problem with our assumptions is that we purchased the duplex with cash. Most real estate investors use leverage. (There’s that word again!) They borrow most of the purchase price of the real estate investment. Currently, lenders typically want at least 25% down for investment properties. That means our would-be investor will only need to put $200,000 down. Add about $15,000 for miscellaneous closing costs and we need $215,000 to make the purchase. We will then have $600,000 mortgage which at about 6% will cost us around $3,600 per month. Let’s update the spreadsheet.
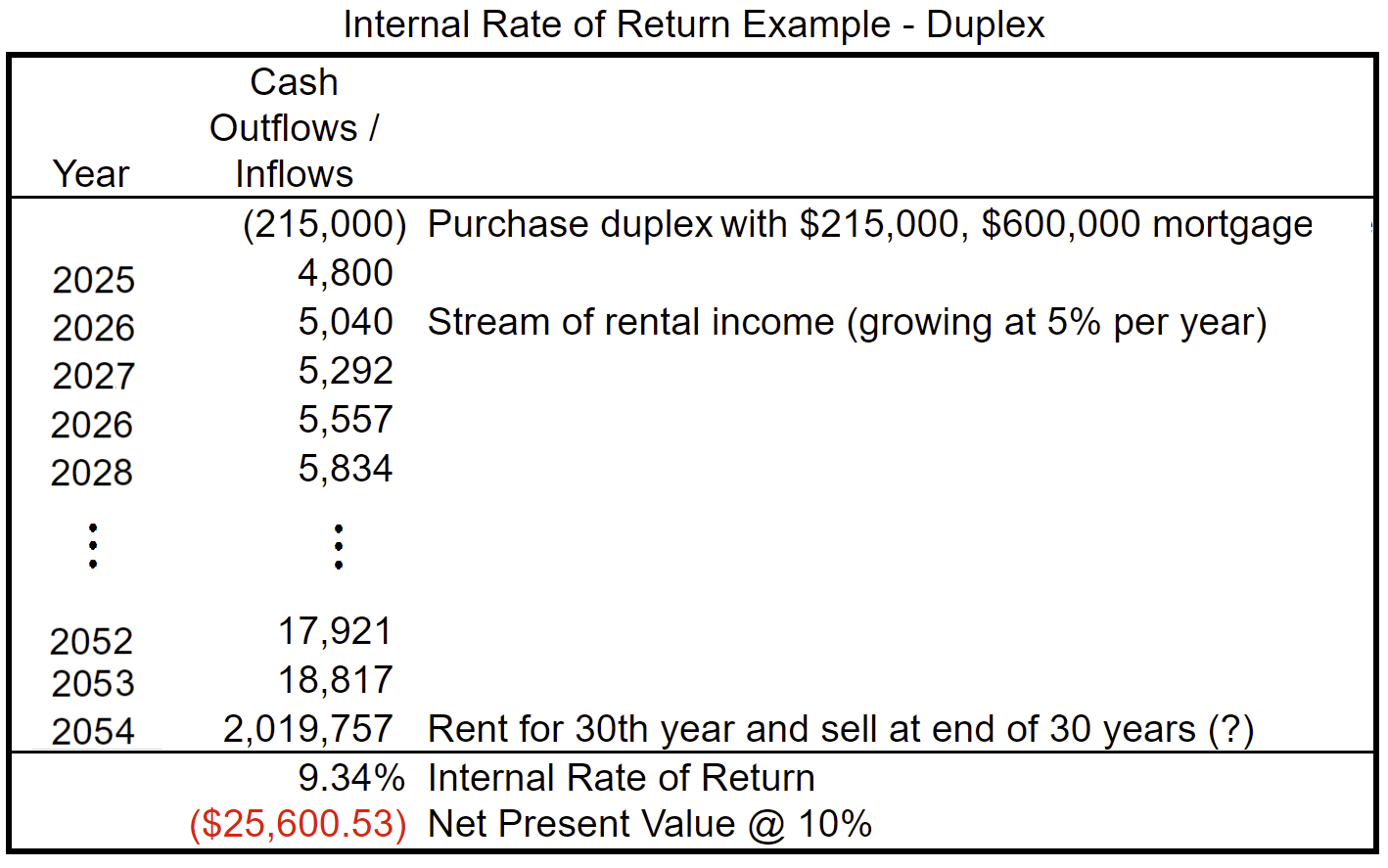
Ooops! Our Internal Rate of Return fell to 9.34% and our Net Present Value is now negative. What happened? We are sharing our investment returns with the bank! The 30-year mortgage reduced our net income substantially from $48,000 to $4,800 in the first year alone. Also, if we are to be realistic, we must come to the conclusion that real estate prices in the San Diego area are simply out of control and we are most likely in yet another real estate bubble. We have been here before and we will be here again. As interest rates rise and a possible recession comes, we can expect prices to fall and in some areas, they will fall hard. Of course, as Sir John Maynard Keynes is reported to have said, “The market can stay irrational longer than you can stay solvent.” We do know that bubbles eventually pop and that is when the opportunities are plenty. Stay tuned!
Note: Recently, many private equity firms such as The Blackstone Group, with hundreds of billions of dollars backing them have been buying local residential real estate properties nationwide. They pay for the properties with cash and have been crowding out the local buyers. Many local advocates have been sounding the alarm about this nationwide trend and are arguing that these private equity firms are putting profits over people. Where does a capitalist society draw the line regarding the welfare of a community and the quest for profits? Again, stay tuned!
Let’s now take a look at investments with a whole lot more zeros at the end of the numbers. Say a local government wants to build a bridge that would increase economic activity dramatically. The city believes that commuters and businesses alike would be more than willing to pay to use the bridge. Let’s say that the bridge will cost $250,000,000 to build. It is initially projected to bring in revenues of $25,000,000 per year and that revenue will increase by 1% each year. However, the projected lifespan of the bridge is only 40 years. It will need be to be dismantled. That is projected to cost $100,000,000 in 40 years. We need to include that cash outflow at the very end of the project’s life. Here is the spreadsheet:

With a required rate of return of 10%, the Net Present Value is positive at over $41 million and the Internal Rate of Return is over 11%. Assuming the bridge is as popular as expected, the bridge will not only be boon to the city’s economy, it will also be economically prosperous for the bridge authority or private company that owns the bridge. This same analysis can be done for water project, factories, airports, nuclear reactors, or any large-scale endeavor that needs significant funding to be built.
Hmmm. Something might have been nagging at you as you worked through this example. Where did the initial $250,000,000 come from to build the bridge? Give yourself a gold star if that is what was nagging at you. Did they hold bake sales at the local schools and churches? No, they sold bonds. We need to include the interest and principal payments for the bonds in our analysis. Also, the bridge authority is going to have to build up funds for the dismantling of the bridge after the 40 years. Do these types of investments pique your interest? If so, there is a future for you in corporate and municipal finance, Dear Students!
Last, we must address an issue with the Internal Rate of Return that is very important. Sometimes, the results from our calculations simply don’t make sense. Sometimes, there is no result. Other times, there is more than one result. When this happens, there are a couple of ways to tackle the problem. At times, we can use our common sense to determine which is the correct result. Other times, we can create a table and graph as we did with our first example. And sometimes, we are just left with no result. Oh, well. This is why the Internal Rate of Return spreadsheet function sometimes comes back with an error message saying it could not find an Internal Rate of Return.
Here is a great example of a common-sense result and an absurd result from the Internal Rate of Return calculations:
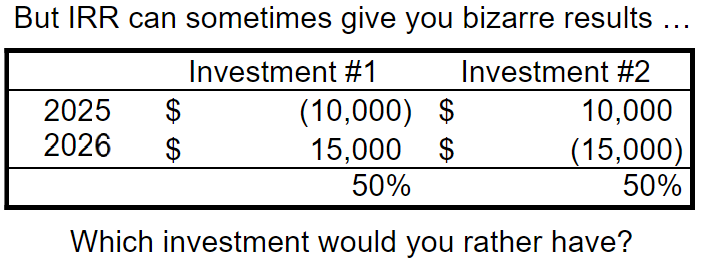
With Investment #1, you pay $10,000 this year and receive $15,000 next year. Pretty darned good, eh? Investment #2 pays you $10,000 this year but you are required to pay back $15,000 next year. Ah, no thanks, you say. However, the calculations for Internal Rate of Return for the two investments both produce an Internal Rate of Return of 50%. The moral of the story is to always check our Internal Rate of Return calculations for common sense results. If in doubt, create a table and graph.
So, what’s the bottom line on Present Value, Net Present Value, and Internal Rate of Return? How does having a spreadsheet change the way we do our calculations? The quick answer is, “Not much!” But spreadsheets make calculating Present Value or Net Present Value, whichever you prefer, and Internal Rate of Return much, much easier and faster. And it gives you an extremely precise result when calculating your rate of return from a stream of future income, which is exactly what we do not want you to rely on!
“Uh, why not?” you ask. Because unless you are calculating the return from a very predictable source (example: bonds), precision is your enemy! Never forget that you are predicting the future and as the old saying goes, “Prediction is difficult, especially about the future!” (You really were not expecting us to end without warning you yet again to never put too much faith in our predictions, right?)


