2.3: Simple and Compound Interest
- Page ID
- 45783
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning outcome
- Calculate simple and compound interest
When a person takes out a loan, most lenders charge interest on the loan. Interest is a fee or change for borrowing money, typically a percent rate charged per year. We can compute simple interest by finding the interest rate percentage of the amount borrowed, then multiply by the number of years interest is earned. Another type of interest calculates interest on both the money initially deposited as well as the interest money earned, and is called compound interest. We’ll start with simple interest.
Simple Interest Equation
\(I=p\cdot{r}\cdot{t}\)
Where:
\(I\) is the interest paid
\(p\) is the principal—the original amount of money borrowed
\(r\) is the interest rate, a per-year rate, written as a decimal
\(t\) is the time of the loan, expressed in years or portions of a year
Example
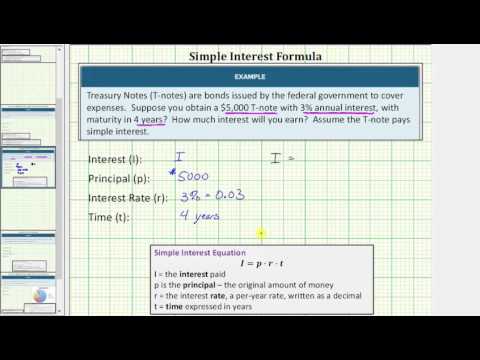
Treasury Notes (T-notes) are bonds issued by the federal government to cover its expenses. Suppose you obtain a \($1,000\) T-note with a \(4\%\) annual rate, with a maturity in \(2\) years. How much interest will you earn?
[reveal-answer q=”694437″]Show Solution[/reveal-answer]
[hidden-answer a=”694437″]
Identify the information given in the problem.
Interest (\(I\)): unknown
Principal (\(p\)): \($1000\)
Rate (\(r\)): \(4\%=0.04\)
Time (\(t\)): \(2\) years
Put the information in the simple interest equation.
\(I=1000\cdot0.04\cdot2\)
Multiply.
\(I=80\)
Answer
You would earn \($80\) in interest.
[/hidden-answer]
In the following video, you are shown how to find how much interest is earned on a specified investment amount.
Example
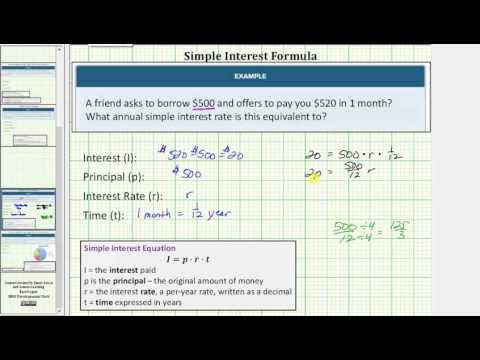
A friend asks to borrow \($240\), offering to repay you \($250\) in 1 month. What annual interest rate is this equivalent to?
[reveal-answer q=”470866″]Show Solution[/reveal-answer]
[hidden-answer a=”470866″]
Identify the information given in the problem. Here your friend is paying back $10 more than he borrowed, so that is the interest paid.
Interest (\(I\)): \($10\)
Principal (\(p\)): \($240\)
Rate (\(r\)): unknown
Time (\(t\)): \(1\) month
Convert the time to years.
\(1\,\,\text{month}=\frac{1}{12}\,\,\text{year}\)
Put the information in the simple interest equation.
\(10=240\cdot{r}\cdot\frac{1}{12}\)
Regroup and simplify.
\(\begin{array}{l}10=r\cdot240\cdot\frac{1}{12}\\\\10=r\cdot\frac{240}{12}\\\\10=r\cdot20\end{array}\)
Divide to undo the multiplication.
\(r=10\div20=0.50\)
Rewrite as a percent.
\(0.50=50\%\)
Answer
This is equivalent to a \(50\%\) annual interest rate.
[/hidden-answer]
The example video that follows shows how to determine the annual simple interest rate.
Applications with simple interest usually involve either investing money or borrowing money. To solve these applications, we continue to use the same strategy for applications that we have used earlier in this chapter. The only difference is that in place of translating to get an equation, we can use the simple interest formula. We will provide examples of how to find interest earned, calculate the rate of interest, and how to find the principal given a rate and the interest earned.
We will start by solving a simple interest application to find the interest.
example
Nathaly deposited \(\text{\$12,500}\) in her bank account where it will earn \(\text{4%}\) interest. How much interest will Nathaly earn in \(5\) years?
Solution
We are asked to find the interest, \(I\).
Organize the given information in a list.
\(I=?\)
\(p = $12,500\)
\(r =4\%\)
\(t =5\) years
| Write the formula. | \(I=Prt\) |
| Substitute the given information. | \(I=\left(12,500\right)\left(0.04\right)\left(5\right)\) |
| Simplify. | \(I=2,500\) |
| Check your answer. Is \(\text{\$2,500}\) a reasonable interest on \(\text{\$12,500}\) over \(5\) years? | |
| At \(4\text{%}\) interest per year, in \(5\) years the interest would be \(20\text{%}\) of the principal. Is \(20\text{%}\) of \(\text{\$12,500}\) equal to \(\text{\$2,500}\)? Yes. | |
| Write a complete sentence that answers the question. | The interest is \(\text{\$2,500}\). |
try it
[ohm_question]146792[/ohm_question]
There may be times when you know the amount of interest earned on a given principal over a certain length of time, but you don’t know the rate. For instance, this might happen when family members lend or borrow money among themselves instead of dealing with a bank. In the next example, we’ll show how to solve for the rate.
example
Loren lent his brother \($3,000\) to help him buy a car. In \(\text{4 years}\) his brother paid him back the \($3,000\) plus \($660\) in interest. What was the rate of interest?
[reveal-answer q=”361018″]Show Answer[/reveal-answer]
[hidden-answer a=”361018″]
Solution
We are asked to find the rate of interest, \(r\).
Organize the given information.
\(I=660\)
\(P=$3,000\)
\(r=?\)
\(t=4\) years
| Write the formula. | \(I=Prt\) |
| Substitute the given information. | \(660=\left(3,000\right)r\left(4\right)\) |
| Multiply. | \(660=\left(12,000\right)r\) |
| Divide. | \(\Large\frac{660}{12,000}\normalsize=\Large\frac{\left(12,000\right)r}{12,000}\) |
| Simplify. | \(0.055=r\) |
| Change to percent form. | \(5.5\%=r\) |
| Check your answer. Is \(5.5\%\) a reasonable interest rate to pay your brother? | |
| \(I=Prt\) | |
| \(660\stackrel{?}{=}\left(3,000\right)\left(0.055\right)\left(4\right)\) | |
| \(660=660\quad\checkmark\) | |
| Write a complete sentence that answers the question. | The rate of interest was \(5.5\%\). |
[/hidden-answer]
try it
[ohm_question]146793[/ohm_question]
In the next video we use the simple interest formula to find the rate of interest given an amount of money borrowed and the amount if interest paid.
There may be times when you take a loan for a large purchase and the amount of the principal is not clear. This might happen, for instance, in making a car purchase when the dealer adds the cost of a warranty to the price of the car. In the next example, we will solve a simple interest application for the principal.
example
Eduardo noticed that his new car loan papers stated that with an interest rate of \(\text{7.5%}\), he would pay \(\text{\$6,596.25}\) in interest over \(5\) years. How much did he borrow to pay for his car?
[reveal-answer q=”754756″]Show Answer[/reveal-answer]
[hidden-answer a=”754756″]
Solution
We are asked to find the principal, \(P\).
Organize the given information.
\(\begin{array}{ccc}\hfill I& =& 6,596.25\hfill \\ \hfill P& =& ?\hfill \\ \hfill r& =& \text{7.5%}\hfill \\ \hfill t& =& \text{5 years}\hfill \end{array}\)
| Write the formula. | \(I=Prt\) |
| Substitute the given information. | \(6,596.25=P\left(0.075\right)\left(5\right)\) |
| Multiply. | \(6,596.25=0.375P\) |
| Divide. | \(\Large\frac{6,596.25}{0.375}\normalsize=\Large\frac{0.375P}{0.375}\) |
| Simplify. | \(17,590=P\) |
| Check your answer. Is \(\text{\$17,590}\) a reasonable amount to borrow to buy a car? | |
| \(I=Prt\) | |
| \(6,596.25\stackrel{?}{=}\left(17,590\right)\left(0.075\right)\left(5\right)\) | |
| \(6,596.25=6,596.25\quad\checkmark\) | |
| Write a complete sentence that answers the question. | The amount borrowed was \($17,590\). |
[/hidden-answer]
TRY IT
[ohm_question]146794[/ohm_question]
In the simple interest formula, the rate of interest is given as an annual rate, the rate for one year. So the units of time must be in years. If the time is given in months, we convert it to years.
example
Caroline got \($900\) as graduation gifts and invested it in a \(10\)-month certificate of deposit that earned \(2.1\%\) interest. How much interest did this investment earn?
[reveal-answer q=”799758″]Show Answer[/reveal-answer]
[hidden-answer a=”799758″]
Solution
We are asked to find the interest, \(I\).
Organize the given information.
\(\begin{array}{ccc}\hfill I& =& ?\hfill \\ \hfill P& =& \text{\$900}\hfill \\ \hfill r& =& \text{2.1%}\hfill \\ \hfill t& =& \text{10 months}\hfill \end{array}\)
| Write the formula. | \(I=Prt\) |
| Substitute the given information, converting 10 months to \(\Large\frac{10}{12}\) of a year. | \(I=$900\left(0.021\right)\left(\Large\frac{10}{12}\normalsize\right)\) |
| Multiply. | \(I=15.75\) |
| Check your answer. Is \(\text{\$15.75}\) a reasonable amount of interest? | |
| If Caroline had invested the \(\text{\$900}\) for a full year at \(2\text{%}\) interest, the amount of interest would have been \(\text{\$18}\). Yes, \(\text{\$15.75}\) is reasonable. | |
| Write a complete sentence that answers the question. | The interest earned was \(\text{\$15.75}\). |
[/hidden-answer]
try it
[ohm_question]146796[/ohm_question]
In the following video we show an example of how to calculate the amount of interest earned on a treasury note.
THE COMPOUND INTEREST FORMULA
Compound interest can be calculated using the formula
\(A(t)=P(1+r)^{t}\)
where
- A(t) is the account value,
- t is measured in years,
- P is the starting amount of the account, often called the principal, or more generally present value,
- r is the annual percentage rate (APR) expressed as a decimal, and assuming the interest is only compounded once a year
In our next example we will calculate the value of an account after ten years of interest compounded annually.
Example
If we invest \($3,000\) in an investment account paying \(3\%\) interest compounded annually, how much will the account be worth in \(10\) years?
[reveal-answer q=”689928″]Show Answer[/reveal-answer]
[hidden-answer a=”689928″]
Because we are starting with \($3,000\), \(P= 3000\). Our interest rate is \(3\%\), so \(r=0.03\). We want to know the value of the account in \(10\) years, so we are looking for \(A(10)\), the value when \(t = 10\).
\(\begin{array}{c}A\left(t\right)\hfill & =P\left(1+r\right)^{t}\hfill & \text{Use the compound interest formula}. \\ A\left(10\right)\hfill & =3000\left(1+0.03\right)^{10}\hfill & \text{Substitute using given values}. \\ \text{ }\hfill & \approx 4031.75\hfill & \text{Round to two decimal places}.\end{array}\)
The account will be worth about \($4,031.75\) in \(10\) years.
[/hidden-answer]
Sometimes you will be asked for the final total amount in an account after interest is added. Make sure that after you solve for interest earned, you add it back onto the principal to get the total amount.
TRY IT
[ohm_question]2556[/ohm_question]
Now we will look at an example that uses the compound interest formula to solve for the principal.
Example
A 529 Plan is a college-savings plan that allows relatives to invest money to pay for a child’s future college tuition; the account grows tax-free. Lily wants to set up a 529 account for her new granddaughter and wants the account to grow to \($40,000\) over \(18\) years. She believes the account will earn 6% compounded annually. To the nearest dollar, how much will Lily need to invest in the account now?
[reveal-answer q=”254680″]Show Answer[/reveal-answer]
[hidden-answer a=”254680″]
The nominal interest rate is \(6\%\), so \(r=0.06\)
We want to find the initial investment, \(P\), needed so that the value of the account will be worth \($40,000\) in \(18\) years. Substitute the given values into the compound interest formula, and solve for \(P\).
\(\begin{array}{c}A\left(t\right)\hfill & =P{\left(1+r\right)}^{t}\hfill & \text{Use the compound interest formula}.\hfill \\ 40,000\hfill & =P{\left(1+0.06\right)}^{18}\hfill & \text{Substitute using given values }A\text{, }r, n\text{, and }t.\hfill \\ 40,000\hfill & =P{\left(1.06\right)}^{18}\hfill & \text{Simplify}.\hfill \\ \frac{40,000}
Callstack:
at (Bookshelves/Accounting/Accounting_for_Managers_(Lumen)/02:_Calculations_and_Solving_Equations/2.03:_Simple_and_Compound_Interest), /content/body/div[5]/div[3]/p[5]/span, line 1, column 1
Lily will need to invest \($14,013.75\) to have \($40,000\) in \(18\) years.
[/hidden-answer]
TRY IT
[ohm_question]157038[/ohm_question]