2.2: Discount Problems
- Page ID
- 45782
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning outcome
- Use mathematical notation to solve discount problems

A store called Feminine Furnishings is having a sale on bedding. Their queen sheet sets have a list price of \($126\). During the first two weeks of February, the store has a—Snuggle Up In Love Sale— where customers save \(14\%\) on any white, pink, or red bedding set. Carly selects a bedding set with pink stripes and pays \($108.36\).
Applications of discount are very common in retail settings. When you buy an item on sale, the original or list price of the item has been reduced by some dollar amount. The discount rate, usually given as a percent, is used to determine the amount of the discount. To determine the amount of discount, we multiply the discount rate by the original price. We summarize the discount model in the box below.
Discount
An amount of discount is subtracted from the original price.
amount of discount = discount rate \(\cdot\) original price
sale price = original price \(-\) discount
The sale price should always be less than the original price.
In some cases, the amount of discount is a fixed dollar amount. Then we just find the sale price by subtracting the amount of discount from the original price. For example, as you walk into a store you may see a sign that says “Spend \($100\) or more, and receive a \($20\) discount!”
example
Jason bought a pair of sunglasses from a rack that was labeled \(\text{\$10}\) off all Retrop brand glasses. The original price of the sunglasses was \(\text{\$39}\). What was the sale price of the sunglasses?
[reveal-answer q=”967734″]Show Answer[/reveal-answer]
[hidden-answer a=”967734″]
Solution
| Identify what you are asked to find. | What is the sale price? |
| Choose a variable to represent it. | Let \(s=\) the sale price. |
| Write a sentence that gives the information to find it. | The sale price is the original price minus the discount. |
| Translate into an equation. |  |
| Simplify. | \(s=29\) |
| Check if this answer is reasonable. | |
| Yes. The sale price, \(\text{\$29}\), is less than the original price, \(\text{\$39}\). | |
| Write a complete sentence that answers the question. | The sale price of the sunglasses was \(\text{\$29}\). |
[/hidden-answer]
try it
[ohm_question]146772[/ohm_question]
In the first example, the amount of discount was a set or static amount. In the next example, the discount is given as a percent of the original price.
Example
Elise bought a dress that was discounted \(\text{35%}\) off of the original price of \(\text{\$140}\). What was the amount of discount and the sale price of the dress?
[reveal-answer q=”967374″]Show Answer[/reveal-answer]
[hidden-answer a=”967374″]
Solution
ⓐ Before beginning, you may find it helpful to organize the information in a list.
Original price = \(\text{\$140}\)
Discount rate = \(35\text{%}\)
Amount of discount = ?
| Identify what you are asked to find. | What is the amount of discount? |
| Choose a variable to represent it. | Let \(d=\) the amount of discount. |
| Write a sentence that gives the information to find it. | The discount is \(35\text{%}\) of the original price. |
| Translate into an equation. | 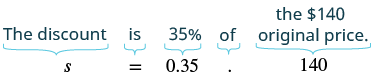 |
| Simplify. | \(d=49\) |
| Check if this answer is reasonable. | |
| Yes. A \(\text{\$49}\) discount is reasonable for a \(\text{\$140}\) dress. | |
| Write a complete sentence that answers the question. | The amount of discount was \(\text{\$49}\). |
ⓑ
Original price = \(\text{\$140}\)
Amount of discount = \(\text{\$49}\)
Sale price = ?
| Identify what you are asked to find. | What is the sale price of the dress? |
| Choose a variable to represent it. | Let \(s=\) the sale price. |
| Write a sentence that gives the information to find it. | The sale price is the original price minus the discount. |
| Translate into an equation. |  |
| Simplify. | \(s=91\) |
| Check if this answer is reasonable. | |
| Yes. The sale price, \(\text{\$91}\), is less than the original price, \(\text{\$140}\). | |
| Write a complete sentence that answers the question. | The sale price of the dress was \(\text{\$91}\). |
[/hidden-answer]
try it
[ohm_question]146775[/ohm_question]
There may be times when you buy something on sale and want to know the discount rate. The next example will show this case.
example
Jeannette bought a swimsuit at a sale price of \(\text{\$13.95}\). The original price of the swimsuit was \(\text{\$31}\). Find the ⓐ amount of discount and ⓑ discount rate.
[reveal-answer q=”123339″]Show Answer[/reveal-answer]
[hidden-answer a=”123339″]
Solution
ⓐ Before beginning, you may find it helpful to organize the information in a list.
Original price = \(\text{\$31}\)
Amount of discount = ?
Sale price = \(\text{\$13.95}\)
| Identify what you are asked to find. | What is the amount of discount? |
| Choose a variable to represent it. | Let \(d=\) the amount of discount. |
| Write a sentence that gives the information to find it. | The discount is the original price minus the sale price. |
| Translate into an equation. |  |
| Simplify. | \(d=17.05\) |
| Check if this answer is reasonable. | |
| Yes. The \(\text{\$17.05}\) discount is less than the original price. | |
| Write a complete sentence that answers the question. | The amount of discount was \($17.05\). |
ⓑ Before beginning, you may find it helpful to organize the information in a list.
Original price = \($31\)
Amount of discount = \($17.05\)
Discount rate = ?
| Identify what you are asked to find. | What is the discount rate? |
| Choose a variable to represent it. | Let \(r=\) the discount rate. |
| Write a sentence that gives the information to find it. | The discount is what percent of the original price? |
| Translate into an equation. | 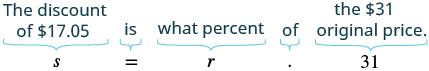 |
| Divide. | \(\Large\frac{17.05}{31}\normalsize =\Large\frac{r(31)}{31}\) |
| Simplify. | \(0.55=r\) |
| Check if this answer is reasonable. | |
| The rate of discount was a little more than \(50\text{%}\) and the amount of discount is a little more than half of \(\text{\$31}\). | |
| Write a complete sentence that answers the question. | The rate of discount was \(55\text{%}\). |
[/hidden-answer]
try it
[ohm_question]156971[/ohm_question]
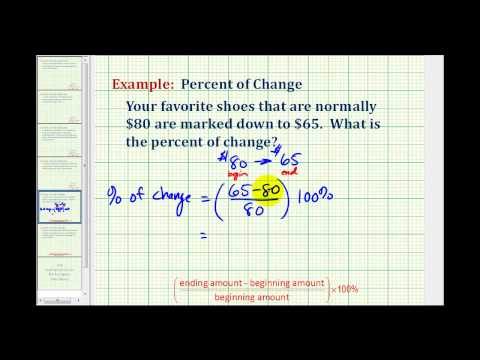
In the following video we show another example of how to find the discount rate (also called the percent of change) given the original price and the marked-down price.