10: ER Modelling
- Page ID
- 78244
Author: Adrienne Watt
One important theory developed for the entity relational (ER) model involves the notion of functional dependency (FD). The aim of studying this is to improve your understanding of relationships among data and to gain enough formalism to assist with practical database design.
Like constraints, FDs are drawn from the semantics of the application domain. Essentially, functional dependencies describe how individual attributes are related. FDs are a kind of constraint among attributes within a relation and contribute to a good relational schema design. In this chapter, we will look at:
- The basic theory and definition of functional dependency
- The methodology for improving schema designs, also called normalization
Relational Design and Redundancy
Generally, a good relational database design must capture all of the necessary attributes and associations. The design should do this with a minimal amount of stored information and no redundant data.
In database design, redundancy is generally undesirable because it causes problems maintaining consistency after updates. However, redundancy can sometimes lead to performance improvements; for example, when redundancy can be used in place of a join to connect data. A join is used when you need to obtain information based on two related tables.
Consider Figure 10.1: customer 1313131 is displayed twice, once for account no. A-101 and again for account A-102. In this case, the customer number is not redundant, although there are deletion anomalies with the table. Having a separate customer table would solve this problem. However, if a branch address were to change, it would have to be updated in multiple places. If the customer number was left in the table as is, then you wouldn’t need a branch table and no join would be required, and performance is improved .

Figure 10.1. An example of redundancy used with bank accounts and branches.
Insertion Anomaly
An insertion anomaly occurs when you are inserting inconsistent information into a table. When we insert a new record, such as account no. A-306 in Figure 10.2, we need to check that the branch data is consistent with existing rows.

Figure 10.2. Example of an insertion anomaly.
Update Anomaly
If a branch changes address, such as the Round Hill branch in Figure 10.3, we need to update all rows referring to that branch. Changing existing information incorrectly is called an update anomaly.

Figure 10.3. Example of an update anomaly.
Deletion Anomaly
A deletion anomaly occurs when you delete a record that may contain attributes that shouldn’t be deleted. For instance, if we remove information about the last account at a branch, such as account A-101 at the Downtown branch in Figure 10.4, all of the branch information disappears.

Figure 10.4. Example of a deletion anomaly.
The problem with deleting the A-101 row is we don’t know where the Downtown branch is located and we lose all information regarding customer 1313131. To avoid these kinds of update or deletion problems, we need to decompose the original table into several smaller tables where each table has minimal overlap with other tables.
Each bank account table must contain information about one entity only, such as the Branch or Customer, as displayed in Figure 10.5.

Figure 10.5. Examples of bank account tables that contain one entity each, by A. Watt.
Following this practice will ensure that when branch information is added or updated it will only affect one record. So, when customer information is added or deleted, the branch information will not be accidentally modified or incorrectly recorded.
Example: employee project table and anomalies
Figure 10.6 shows an example of an employee project table. From this table, we can assume that:
- EmpID and ProjectID are a composite PK.
- Project ID determines Budget (i.e., Project P1 has a budget of 32 hours).

Figure 10.6. Example of an employee project table, by A. Watt.
Next, let’s look at some possible anomalies that might occur with this table during the following steps.
- Action: Add row {S85,35,P1,9}
- Problem: There are two tuples with conflicting budgets
- Action: Delete tuple {S79, 27, P3, 1}
- Problem: Step #3 deletes the budget for project P3
- Action: Update tuple {S75, 32, P1, 7} to {S75, 35, P1, 7}
- Problem: Step #5 creates two tuples with different values for project P1’s budget
- Solution: Create a separate table, each, for Projects and Employees, as shown in Figure 10.7.

Figure 10.7. Solution: separate tables for Project and Employee, by A. Watt.
How to Avoid Anomalies
The best approach to creating tables without anomalies is to ensure that the tables are normalized, and that’s accomplished by understanding functional dependencies. FD ensures that all attributes in a table belong to that table. In other words, it will eliminate redundancies and anomalies.
Example: separate Project and Employee tables

Figure 10.8. Separate Project and Employee tables with data, by A. Watt.
By keeping data separate using individual Project and Employee tables:
- No anomalies will be created if a budget is changed.
- No dummy values are needed for projects that have no employees assigned.
- If an employee’s contribution is deleted, no important data is lost.
- No anomalies are created if an employee’s contribution is added.
Key Terms
deletion anomaly: occurs when you delete a record that may contain attributes that shouldn’t be deleted
functional dependency (FD): describes how individual attributes are related
insertion anomaly: occurs when you are inserting inconsistent information into a table
join: used when you need to obtain information based on two related tables
update anomaly: changing existing information incorrectly
Exercises
- Normalize Figure 10.9.
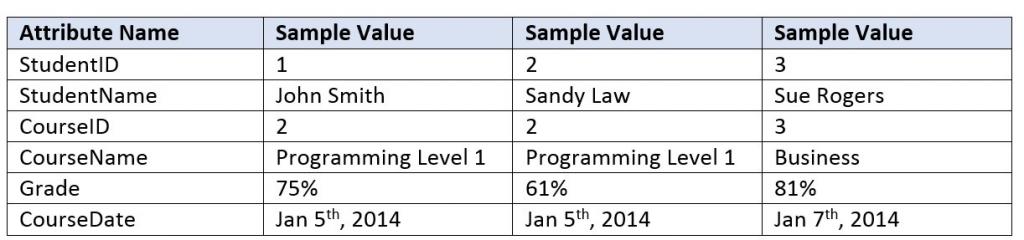
Figure 10.9. Table for question 1, by A. Watt.
- Create a logical ERD for an online movie rental service (no many to many relationships). Use the following description of operations on which your business rules must be based:The online movie rental service classifies movie titles according to their type: comedy, western, classical, science fiction, cartoon, action, musical, and new release. Each type contains many possible titles, and most titles within a type are available in multiple copies. For example, note the following summary:TYPE TITLE
Musical My Fair Lady (Copy 1)
My Fair Lady (Copy 2)
Oklahoma (Copy 1)
Oklahoma (Copy 2)
Oklahoma (Copy 3)
etc. - What three data anomalies are likely to be the result of data redundancy? How can such anomalies be eliminated?
Also see Appendix B: Sample ERD Exercises
Attribution
This chapter of Database Design (including images, except as otherwise noted) is a derivative copy of Relational Design Theory by Nguyen Kim Anh licensed under Creative Commons Attribution License 3.0 license
The following material was written by Adrienne Watt:
- Example: employee project table and anomalies
- How to Avoid Anomalies
- Key Terms
- Exercises

