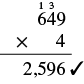1.17: Adding, Subtracting, Multiplying, and Dividing Whole Numbers

Last updated
Save as PDF

Page ID: 45755

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Learning Objectives

Use addition, subtraction, multiplication, and division when evaluating whole number expressions

Working with whole numbers and performing basic calculations is the backbone of all math. We’re going to assume you remember how to do single digit addition, subtraction, multiplication, and division. You will often have a calculator on hand to do these calculations, but a quick refresher will help you better understand how to work with numbers so that complex equations are less daunting.

Addition

example

Add: $28+61$

Solution
To add numbers with more than one digit, it is often easier to write the numbers vertically in columns.

Write the numbers so the ones and tens digits line up vertically.

$\begin{array}{c}\hfill 28\\ \\ \hfill \underset{\text{____}}{+61}\end{array}$

Then add the digits in each place value.

Add the ones: $8+1=9$

Add the tens: $2+6=8$

$\begin{array}{c}\hfill 28\\ \\ \hfill \underset{\text{____}}{+61}\\ \hfill 89\end{array}$

In the previous example, the sum of the ones and the sum of the tens were both less than $10$ . But what happens if the sum is $10$ or more? Let’s use our base- $10$ model to find out.

The graphic below shows the addition of $17$ and $26$ again.

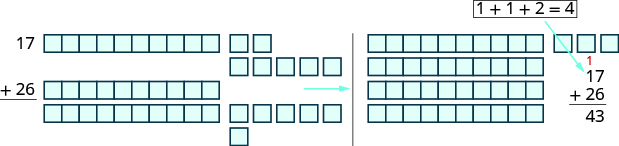
An image containing two groups of items. The left group includes 1 horizontal rod with 10 blocks and 7 individual blocks 2 horizontal rods with 10 blocks each and 6 individual blocks. The label to the left of this group of items is

When we add the ones, $7+6$ , we get $13$ ones. Because we have more than $10$ ones, we can exchange $10$ of the ones for $1$ ten. Now we have $4$ tens and $3$ ones. Without using the model, we show this as a small red $1$ above the digits in the tens place.

When the sum in a place value column is greater than $9$ , we carry over to the next column to the left. Carrying is the same as regrouping by exchanging. For example, $10$ ones for $1$ ten or $10$ tens for $1$ hundred.

Add whole numbers

Write the numbers so each place value lines up vertically.
Add the digits in each place value. Work from right to left starting with the ones place. If a sum in a place value is more than $9$ , carry to the next place value.
Continue adding each place value from right to left, adding each place value and carrying if needed.

example

Add: $43+69$
[reveal-answer q=”61333″]Show Answer[/reveal-answer]
[hidden-answer a=”61333″]

Solution

Write the numbers so the digits line up vertically.	$\begin{array}{c}\hfill 43\\ \\ \hfill \underset{\text{____}}{+69}\end{array}$
Add the digits in each place. Add the ones: $3+9=12$
Write the $2$ in the ones place in the sum. Add the $1$ ten to the tens place.	$\begin{array}{c}\hfill \stackrel{1}{4}3\\ \hfill \underset{\text{____}}{+69}\\ \hfill 2\end{array}$
Now add the tens: $1+4+6=11$ Write the 11 in the sum.	$\begin{array}{c}\hfill \stackrel{1}{4}3\\ \hfill \underset{\text{____}}{+69}\\ \hfill 112\end{array}$

[/hidden-answer]

try it

[ohm_question]147154[/ohm_question]

try it

[ohm_question]147156[/ohm_question]

When the addends have different numbers of digits, be careful to line up the corresponding place values starting with the ones and moving toward the left.

example

Add: $1,683+479$ .
[reveal-answer q=”603010″]Show Answer[/reveal-answer]
[hidden-answer a=”603010″]

Solution

Write the numbers so the digits line up vertically.	$\begin{array}{c}\hfill 1,683\\ \\ \hfill \underset{\text{______}}{+479}\end{array}$
Add the digits in each place value.
Add the ones: $3+9=12$ . Write the $2$ in the ones place of the sum and carry the $1$ ten to the tens place.	$\begin{array}{c}\hfill 1,6\stackrel{1}{8}3\\ \\ \hfill \underset{\text{______}}{+479}\\ \hfill 2\end{array}$
Add the tens: $1+7+8=16$ Write the $6$ in the tens place and carry the $1$ hundred to the hundreds place.	$\begin{array}{c}\hfill 1,\stackrel{1}{6}\stackrel{1}{8}3\\ \\ \hfill \underset{\text{______}}{+479}\\ \hfill 62\end{array}$
Add the hundreds: $1+6+4=11$ Write the $1$ in the hundreds place and carry the $1$ thousand to the thousands place.	$\begin{array}{c}\hfill \stackrel{1}{1},\stackrel{1}{6}\stackrel{1}{8}3\\ \\ \hfill \underset{\text{______}}{+479}\\ \hfill 162\end{array}$
Add the thousands $1+1=2$ . Write the $2$ in the thousands place of the sum.	$\begin{array}{c}\hfill \stackrel{1}{1},\stackrel{1}{6}\stackrel{1}{8}3\\ \\ \hfill \underset{\text{______}}{+479}\\ \hfill 2,162\end{array}$

[/hidden-answer]

try it

[ohm_question]156996[/ohm_question]

Watch the video below for another example of how to add three whole numbers by lining up place values.

Thumbnail for the embedded element "Example: Adding Whole Numbers"

A YouTube element has been excluded from this version of the text. You can view it online here: http://pb.libretexts.org/afm-2/?p=52

Subtraction

Addition and subtraction are inverse operations. Addition undoes subtraction, and subtraction undoes addition.
We know $7 - 3=4$ because $4+3=7$ . Knowing all the addition number facts will help with subtraction. Then we can check subtraction by adding. In the examples above, our subtractions can be checked by addition.

$7-3=4$	because	$4+3=7$
$13-8=5$	because	$5+8=13$
$43-26=17$	because	$17+26=43$

To subtract numbers with more than one digit, it is usually easier to write the numbers vertically in columns just as we did for addition. Align the digits by place value, and then subtract each column starting with the ones and then working to the left.

Exercise

Subtract and then check by adding: $89 - 61$ .
[reveal-answer q=”656368″]Show Answer[/reveal-answer]
[hidden-answer a=”656368″]

Solution

Write the numbers so the ones and tens digits line up vertically.

$\begin{array}{c}\hfill 89\\ \hfill \underset{\text{____}}{-61}\end{array}$

Subtract the digits in each place value.

Subtract the ones: $9 - 1=8$

Subtract the tens: $8 - 6=2$

$\begin{array}{c}\hfill 89\\ \hfill \underset{\text{____}}{-61}\\ \hfill 28\end{array}$

Check using addition.

$\begin{array}{c}\hfill 28\\ \hfill \underset{\text{____}}{+61}\\ \hfill 89\end{array}\quad\checkmark$

Our answer is correct.

[/hidden-answer]

TRY IT

An interactive or media element has been excluded from this version of the text. You can view it online here: http://pb.libretexts.org/afm-2/?p=52

Subtract whole numbers

Write the numbers so each place value lines up vertically.
Subtract the digits in each place value. Work from right to left starting with the ones place. If the digit on top is less than the digit below, borrow as needed.
Continue subtracting each place value from right to left, borrowing if needed.
Check by adding.

excercise

Subtract: $43 - 26$ .
[reveal-answer q=”491725″]Show Answer[/reveal-answer]
[hidden-answer a=”491725″]

Solution

Write the numbers so each place value lines up vertically.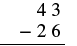
Subtract the ones. We cannot subtract $6$ from $3$ , so we borrow $1$ ten. This makes $3$ tens and $13$ ones. We write these numbers above each place and cross out the original digits.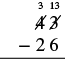
Now we can subtract the ones. $13 - 6=7$ . We write the $7$ in the ones place in the difference.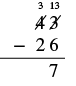
Now we subtract the tens. $3 - 2=1$ . We write the $1$ in the tens place in the difference.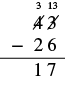
Check by adding. 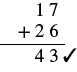Our answer is correct.

[/hidden-answer]

In the example above, if we model subtracting $26$ from $43$ , we would exchange $1$ ten for $10$ ones. When we do this without models, we say we borrow $1$ from the tens place and add $10$ to the ones place.

try it

An interactive or media element has been excluded from this version of the text. You can view it online here: http://pb.libretexts.org/afm-2/?p=52

Exercise

Subtract and then check by adding: $207 - 64$ .
[reveal-answer q=”125839″]Show Answer[/reveal-answer]
[hidden-answer a=”125839″]

Solution

Write the numbers so each place value lines up vertically.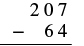
Subtract the ones. $7 - 4=3$ . Write the $3$ in the ones place in the difference. Write the $3$ in the ones place in the difference.
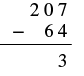Subtract the tens. We cannot subtract $6$ from $0$ so we borrow $1$ hundred and add $10$ tens to the $0$ tens we had. This makes a total of $10$ tens. We write $10$ above the tens place and cross out the $0$ . Then we cross out the $2$ in the hundreds place and write $1$ above it.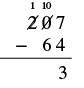
Now we subtract the tens. $10 - 6=4$ . We write the 4 in the tens place in the difference.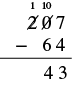
Finally, subtract the hundreds. There is no digit in the hundreds place in the bottom number so we can imagine a $0$ in that place. Since $1 - 0=1$ , we write $1$ in the hundreds place in the difference.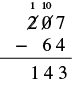
Check by adding. 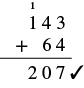Our answer is correct.

[/hidden-answer]

try it

An interactive or media element has been excluded from this version of the text. You can view it online here: http://pb.libretexts.org/afm-2/?p=52

Exercise

Subtract and then check by adding: $2,162 - 479$ .
[reveal-answer q=”61197″]Show Answer[/reveal-answer]
[hidden-answer a=”61197″]

Solution

Write the numbers so each place values line up vertically.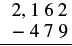
Subtract the ones. Since we cannot subtract $9$ from $2$ , borrow $1$ ten and add $10$ ones to the $2$ ones to make $12$ ones. Write $5$ above the tens place and cross out the $6$ . Write $12$ above the ones place and cross out the $2$ .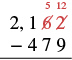
Now we can subtract the ones.	$12 - 9=3$
Write $3$ in the ones place in the difference.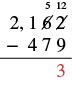
Subtract the tens. Since we cannot subtract $7$ from $5$ , borrow $1$ hundred and add $10$ tens to the $5$ tens to make $15$ tens. Write $0$ above the hundreds place and cross out the $1$ . Write $15$ above the tens place.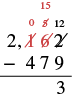
Now we can subtract the tens.	$15 - 7=8$
Write $8$ in the tens place in the difference.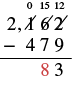
Now we can subtract the hundreds.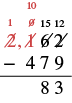
Write $6$ in the hundreds place in the difference.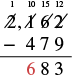
Subtract the thousands. There is no digit in the thousands place of the bottom number, so we imagine a $0$ . $1 - 0=1$ . Write $1$ in the thousands place of the difference.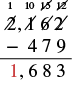
Check by adding. $\begin{array}{}\\ \stackrel{1}{1},\stackrel{1}{6}\stackrel{1}{8}3\hfill \\ \underset{\text{______}}{+479}\hfill \\ 2,162\quad\checkmark \hfill \end{array}\quad\checkmark$

Our answer is correct.

[/hidden-answer]

try it

An interactive or media element has been excluded from this version of the text. You can view it online here: http://pb.libretexts.org/afm-2/?p=52

Watch the video below to see another example of subtracting whole numbers by lining up place values.

Thumbnail for the embedded element "Example: Subtracting Whole Numbers"

A YouTube element has been excluded from this version of the text. You can view it online here: http://pb.libretexts.org/afm-2/?p=52

Multiplication

In order to multiply without using models, you need to know all the one digit multiplication facts. Make sure you know them fluently before proceeding in this section. The table below shows the multiplication facts.

Each box shows the product of the number down the left column and the number across the top row. If you are unsure about a product, model it. It is important that you memorize any number facts you do not already know so you will be ready to multiply larger numbers.

$×$	$0$	$1$	$2$	$3$	$4$	$5$	$6$	$7$	$8$	$9$
$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$0$
$1$	$0$	$1$	$2$	$3$	$4$	$5$	$6$	$7$	$8$	$9$
$2$	$0$	$2$	$4$	$6$	$8$	$10$	$12$	$14$	$16$	$18$
$3$	$0$	$3$	$6$	$9$	$12$	$15$	$18$	$21$	$24$	$27$
$4$	$0$	$4$	$8$	$12$	$16$	$20$	$24$	$28$	$32$	$36$
$5$	$0$	$5$	$10$	$15$	$20$	$25$	$30$	$35$	$40$	$45$
$6$	$0$	$6$	$12$	$18$	$24$	$30$	$36$	$42$	$48$	$54$
$7$	$0$	$7$	$14$	$21$	$28$	$35$	$42$	$49$	$56$	$63$
$8$	$0$	$8$	$16$	$24$	$32$	$40$	$48$	$56$	$64$	$72$
$9$	$0$	$9$	$18$	$27$	$36$	$45$	$54$	$63$	$72$	$81$

We know that changing the order of addition does not change the sum. We saw that $8+9=17$ is the same as $9+8=17$ .

Is this also true for multiplication? Let’s look at a few pairs of factors.

$4\cdot 7=28\quad 7\cdot 4=28$
$9\cdot 7=63\quad 7\cdot 9=63$
$8\cdot 9=72\quad 9\cdot 8=72$

When the order of the factors is reversed, the product does not change. This is called the Commutative Property of Multiplication.

Commutative Property of Multiplication

Changing the order of the factors does not change their product.

$a\cdot b=b\cdot a$

example

Multiply:

$8\cdot 7$
$7\cdot 8$

[reveal-answer q=”468629″]Show Answer[/reveal-answer]
[hidden-answer a=”468629″]

Solution:

1.	$8\cdot 7$
Multiply.	$56$
2.	$7\cdot 8$
Multiply.	$56$

Changing the order of the factors does not change the product.

[/hidden-answer]

try it

An interactive or media element has been excluded from this version of the text. You can view it online here: http://pb.libretexts.org/afm-2/?p=52

To multiply numbers with more than one digit, it is usually easier to write the numbers vertically in columns just as we did for addition and subtraction.

$\begin{array}{c}\hfill 27\\ \hfill \underset{\text{___}}{\times 3}\end{array}$

We start by multiplying $3$ by $7$ .

$3\times 7=21$

We write the $1$ in the ones place of the product. We carry the $2$ tens by writing $2$ above the tens place.

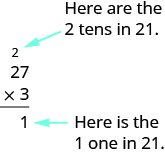
No Alt Text
Then we multiply the $3$ by the $2$ , and add the $2$ above the tens place to the product. So $3\times 2=6$ , and $6+2=8$ . Write the $8$ in the tens place of the product.

No Alt Text
The product is $81$ .

When we multiply two numbers with a different number of digits, it’s usually easier to write the smaller number on the bottom. You could write it the other way, too, but this way is easier to work with.

example

Multiply: $15\cdot 4$

[reveal-answer q=”942773″]Show Answer[/reveal-answer]
[hidden-answer a=”942773″]

Solution

Write the numbers so the digits $5$ and $4$ line up vertically.	$\begin{array}{c}\hfill 15\\ \hfill \underset{\text{_____}}{\times 4}\end{array}$
Multiply $4$ by the digit in the ones place of $15$ . $4\cdot 5=20$ .
Write $0$ in the ones place of the product and carry the $2$ tens.	$\begin{array}{c}\hfill \stackrel{2}{1}5\\ \hfill \underset{\text{_____}}{\times 4}\\ \hfill 0\end{array}$
Multiply $4$ by the digit in the tens place of $15$ . $4\cdot 1=4$ . Add the $2$ tens we carried. $4+2=6$ .
Write the $6$ in the tens place of the product.	$\begin{array}{c}\hfill \stackrel{2}{1}5\\ \hfill \underset{\text{_____}}{\times 4}\\ \hfill 60\end{array}$

[/hidden-answer]

try it

An interactive or media element has been excluded from this version of the text. You can view it online here: http://pb.libretexts.org/afm-2/?p=52

example

Multiply: $286\cdot 5$

[reveal-answer q=”849168″]Show Answer[/reveal-answer]
[hidden-answer a=”849168″]

Solution

Write the numbers so the digits $5$ and $6$ line up vertically.	$\begin{array}{c}\hfill 286\\ \hfill \underset{\text{_____}}{\times 5}\end{array}$
Multiply $5$ by the digit in the ones place of $286$ . $5\cdot 6=30$
Write the $0$ in the ones place of the product and carry the $3$ to the tens place.Multiply $5$ by the digit in the tens place of $286$ . $5\cdot 8=40$	$\begin{array}{}\\ \hfill 2\stackrel{3}{8}6\\ \hfill \underset{\text{_____}}{\times 5}\\ \hfill 0\end{array}$
Add the $3$ tens we carried to get $40+3=43$ . Write the $3$ in the tens place of the product and carry the $4$ to the hundreds place.	$\begin{array}{c}\hfill \stackrel{4}{2}\stackrel{3}{8}6\\ \hfill \underset{\text{_____}}{\times 5}\\ \hfill 30\end{array}$
Multiply $5$ by the digit in the hundreds place of $286$ . $5\cdot 2=10$ . Add the $4$ hundreds we carried to get $10+4=14$ . Write the $4$ in the hundreds place of the product and the $1$ to the thousands place.	$\begin{array}{c}\hfill \stackrel{4}{2}\stackrel{3}{8}6\\ \hfill \underset{\text{_____}}{\times 5}\\ \hfill 1,430\end{array}$

[/hidden-answer]

try it

An interactive or media element has been excluded from this version of the text. You can view it online here: http://pb.libretexts.org/afm-2/?p=52

When we multiply by a number with two or more digits, we multiply by each of the digits separately, working from right to left. Each separate product of the digits is called a partial product. When we write partial products, we must make sure to line up the place values.

MultiplIcation of whole numbers

Write the numbers so each place value lines up vertically.
Multiply the digits in each place value.
- Work from right to left, starting with the ones place in the bottom number.
  - Multiply the bottom number by the ones digit in the top number, then by the tens digit, and so on.
  - If a product in a place value is more than $9$ , carry to the next place value.
  - Write the partial products, lining up the digits in the place values with the numbers above.
- Repeat for the tens place in the bottom number, the hundreds place, and so on.
- Insert a zero as a placeholder with each additional partial product.
Add the partial products.

example

Multiply: $62\left(87\right)$

[reveal-answer q=”698602″]Show Answer[/reveal-answer]
[hidden-answer a=”698602″]

Solution

Write the numbers so each place lines up vertically.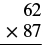
Start by multiplying 7 by 62. Multiply 7 by the digit in the ones place of 62. $7\cdot 2=14$ . Write the 4 in the ones place of the product and carry the 1 to the tens place.
Multiply 7 by the digit in the tens place of 62. $7\cdot 6=42$ . Add the 1 ten we carried. $42+1=43$ latex]. Write the 3 in the tens place of the product and the 4 in the hundreds place.
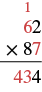The first partial product is $434$ .
Now, write a $0$ under the $4$ in the ones place of the next partial product as a placeholder since we now multiply the digit in the tens place of $87$ by $62$ . Multiply $8$ by the digit in the ones place of $62$ $8\cdot 2=16$ . Write the $6$ in the next place of the product, which is the tens place. Carry the $1$ to the tens place.
Multiply $8$ by $6$ , the digit in the tens place of $62$ , then add the $1$ ten we carried to get $49$ . Write the $9$ in the hundreds place of the product and the $4$ in the thousands place.
The second partial product is $4960$ . Add the partial products.

The product is $5,394$ .

[/hidden-answer]

try it

An interactive or media element has been excluded from this version of the text. You can view it online here: http://pb.libretexts.org/afm-2/?p=52

When there are three or more factors, we multiply the first two and then multiply their product by the next factor. For example:

to multiply	$8\cdot 3\cdot 2$
first multiply $8\cdot 3$	$24\cdot 2$
then multiply $24\cdot 2$	$48$

In the video below, we summarize the concepts presented on this page including the multiplication property of zero, the identity property of multiplication, and the commutative property of multiplication.m

Thumbnail for the embedded element "Multiplying Whole Numbers"

A YouTube element has been excluded from this version of the text. You can view it online here: http://pb.libretexts.org/afm-2/?p=52

Division

We said that addition and subtraction are inverse operations because one undoes the other. Similarly, division is the inverse operation of multiplication. We know $12\div 4=3$ because $3\cdot 4=12$ . Knowing all the multiplication number facts is very important when doing division.

We check our answer to division by multiplying the quotient by the divisor to determine if it equals the dividend. We know $24\div 8=3$ is correct because $3\cdot 8=24$ .

example

Divide. Then check by multiplying.

$42\div 6$
$\frac{72}{9}$
$7\overline{)63}$

Solution:

1.
	$42\div 6$
Divide $42$ by $6$ .	$7$
Check by multiplying. $7\cdot 6$
$42\quad\checkmark$

2.
	$\frac{72}{9}$
Divide $72$ by $9$ .	$8$
Check by multiplying. $8\cdot 9$
$72\quad\checkmark$

3.
	$7\overline{)63}$
Divide $63$ by $7$ .	$9$
Check by multiplying. $9\cdot 7$
$63\quad\checkmark$

try it

[ohm_question]144463[/ohm_question]

What is the quotient when you divide a number by itself?

$\frac{15}{15}=1\text{ because }1\cdot 15=15$

Dividing any number $\text{(except 0)}$ by itself produces a quotient of $1$ . Also, any number divided by $1$ produces a quotient of the number. These two ideas are stated in the Division Properties of One.

Division Properties of One

Any number (except 0) divided by itself is one.	$a\div a=1$
Any number divided by one is the same number.	$a\div 1=a$

example

Divide. Then check by multiplying:

$11\div 11$
$\frac{19}{1}$

[reveal-answer q=”519474″]Show Answer[/reveal-answer]
[hidden-answer a=”519474″]

Solution:

1.
	$11\div 11$
A number divided by itself is $1$ .	$1$
Check by multiplying. $1\cdot 11$
$11\quad\checkmark$

2.
	$\frac{19}{1}$
A number divided by $1$ equals itself.	$19$
Check by multiplying. $19\cdot 1$
$19\quad\checkmark$

[/hidden-answer]

try it

[ohm_question]144635[/ohm_question]

Suppose we have $\text{\$0}$ , and want to divide it among $3$ people. How much would each person get? Each person would get $\text{\$0}$ . Zero divided by any number is $0$ .

Now suppose that we want to divide $\text{\$10}$ by $0$ . That means we would want to find a number that we multiply by $0$ to get $10$ . This cannot happen because $0$ times any number is $0$ . Division by zero is said to be undefined.

These two ideas make up the Division Properties of Zero.

Division Properties of Zero

Zero divided by any number is $0$ .	$0\div a=0$
Dividing a number by zero is undefined.	$a\div 0$ undefined

Another way to explain why division by zero is undefined is to remember that division is really repeated subtraction. How many times can we take away $0$ from $10?$ Because subtracting $0$ will never change the total, we will never get an answer. So we cannot divide a number by $0$ .

example

Divide. Check by multiplying:

$0\div 3$
$\frac{10}{0}$

[reveal-answer q=”208505″]Show Answer[/reveal-answer]
[hidden-answer a=”208505″]

Solution

1.
	$0\div 3$
Zero divided by any number is zero.	$0$
Check by multiplying. $0\cdot 3$
$0\quad\checkmark$

2.
	$10/0$
Division by zero is undefined.	undefined

[/hidden-answer]

try it

[ohm_question]144478[/ohm_question]

When the divisor or the dividend has more than one digit, it is usually easier to use the $4\overline{)12}$ notation. This process is called long division. Let’s work through the process by dividing $78$ by $3$ .

Divide the first digit of the dividend, $7$ , by the divisor, $3$ .
The divisor $3$ can go into $7$ two times since $2\times 3=6$ . Write the $2$ above the $7$ in the quotient.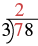
Multiply the $2$ in the quotient by $2$ and write the product, $6$ , under the $7$ .
Subtract that product from the first digit in the dividend. Subtract $7 - 6$ . Write the difference, 1, under the first digit in the dividend.
Bring down the next digit of the dividend. Bring down the $8$ .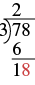
Divide $18$ by the divisor, $3$ . The divisor $3$ goes into $18$ six times.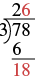
Write $6$ in the quotient above the $8$ .
Multiply the $6$ in the quotient by the divisor and write the product, $18$ , under the dividend. Subtract $18$ from $18$ .

We would repeat the process until there are no more digits in the dividend to bring down. In this problem, there are no more digits to bring down, so the division is finished.

$\text{So }78\div 3=26$ .

Check by multiplying the quotient times the divisor to get the dividend. Multiply $26\times 3$ to make sure that product equals the dividend, $78$ .

$\begin{array}{c}\hfill \stackrel{1}{2}6\\ \hfill \underset{\text{___}}{\times 3}\\ \hfill 78 \end{array}$

It does, so our answer is correct. $\checkmark$

Division of whole numbers

Divide the first digit of the dividend by the divisor.If the divisor is larger than the first digit of the dividend, divide the first two digits of the dividend by the divisor, and so on.
Write the quotient above the dividend.
Multiply the quotient by the divisor and write the product under the dividend.
Subtract that product from the dividend.
Bring down the next digit of the dividend.
Repeat from Step 1 until there are no more digits in the dividend to bring down.
Check by multiplying the quotient times the divisor.

In the video below we show another example of using long division.

Thumbnail for the embedded element "Ex: Long Division - Two Digit Divided by One Digit (No Remainder)"

A YouTube element has been excluded from this version of the text. You can view it online here: http://pb.libretexts.org/afm-2/?p=52

example

Divide $2,596\div 4$ . Check by multiplying:
[reveal-answer q=”252445″]Show Answer[/reveal-answer]
[hidden-answer a=”252445″]

Solution

Let’s rewrite the problem to set it up for long division.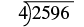
Divide the first digit of the dividend, $2$ , by the divisor, $4$ .
Since $4$ does not go into $2$ , we use the first two digits of the dividend and divide $25$ by $4$ . The divisor $4$ goes into $25$ six times.
We write the $6$ in the quotient above the $5$ .
Multiply the $6$ in the quotient by the divisor $4$ and write the product, $24$ , under the first two digits in the dividend.
Subtract that product from the first two digits in the dividend. Subtract $25 - 24$ . Write the difference, $1$ , under the second digit in the dividend.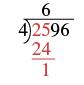
Now bring down the $9$ and repeat these steps. There are $4$ fours in $19$ . Write the $4$ over the $9$ . Multiply the $4$ by $4$ and subtract this product from $19$ .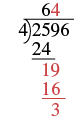
Bring down the $6$ and repeat these steps. There are $9$ fours in $36$ . Write the $9$ over the $6$ . Multiply the $9$ by $4$ and subtract this product from $36$ .
So $2,596\div 4=649$ .
Check by multiplying.

It equals the dividend, so our answer is correct.

[/hidden-answer]

try it

[ohm_question]144636[/ohm_question]

example

Divide $4,506\div 6$ . Check by multiplying:
[reveal-answer q=”474096″]Show Answer[/reveal-answer]
[hidden-answer a=”474096″]

Solution

Let’s rewrite the problem to set it up for long division.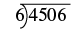
First we try to divide $6$ into $4$ .
Since that won’t work, we try $6$ into $45$ . There are $7$ sixes in $45$ . We write the $7$ over the $5$ .
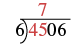Multiply the $7$ by $6$ and subtract this product from $45$ .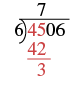
Now bring down the $0$ and repeat these steps. There are $5$ sixes in $30$ . Write the $5$ over the $0$ . Multiply the $5$ by $6$ and subtract this product from $30$ .
Now bring down the $6$ and repeat these steps. There is $1$ six in $6$ . Write the $1$ over the $6$ . Multiply $1$ by $6$ and subtract this product from $6$
Check by multiplying.

It equals the dividend, so our answer is correct.

[/hidden-answer]

try it

[ohm_question]144640[/ohm_question]

Watch this video for another example of how to use long division to divide a four digit whole number by a two digit whole number.

Thumbnail for the embedded element "Example: Dividing Whole Numbers without a Remainder"

A YouTube element has been excluded from this version of the text. You can view it online here: http://pb.libretexts.org/afm-2/?p=52

So far all the division problems have worked out evenly. For example, if we had $24$ cookies and wanted to make bags of $8$ cookies, we would have $3$ bags. But what if there were $28$ cookies and we wanted to make bags of $8?$ Start with the $28$ cookies.

An image of 28 cookies placed at random.
Try to put the cookies in groups of eight.

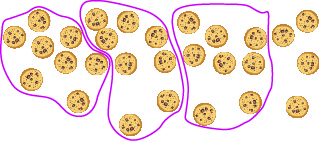
An image of 28 cookies. There are 3 circles, each containing 8 cookies, leaving 3 cookies outside the circles.
There are $3$ groups of eight cookies, and $4$ cookies left over. We call the $4$ cookies that are left over the remainder and show it by writing R4 next to the $3$ . (The R stands for remainder.)

To check this division we multiply $3$ times $8$ to get $24$ , and then add the remainder of $4$ .

$\begin{array}{c}\hfill 3\\ \hfill \underset{\text{___}}{\times 8}\\ \hfill 24\\ \hfill \underset{\text{___}}{+4}\\ \hfill 28\end{array}$

example

Divide $1,439\div 4$ . Check by multiplying.
[reveal-answer q=”498101″]Show Answer[/reveal-answer]
[hidden-answer a=”498101″]

Solution

Let’s rewrite the problem to set it up for long division.
First we try to divide $4$ into $1$ . Since that won’t work, we try $4$ into $14$ . There are $3$ fours in $14$ . We write the $3$ over the $4$ .
Multiply the $3$ by $4$ and subtract this product from $14$ .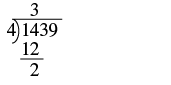
Now bring down the $3$ and repeat these steps. There are $5$ fours in $23$ . Write the $5$ over the $3$ . Multiply the $5$ by $4$ and subtract this product from $23$ .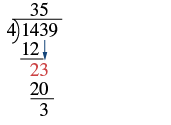
Now bring down the $9$ and repeat these steps. There are $9$ fours in $39$ . Write the $9$ over the $9$ . Multiply the $9$ by $4$ and subtract this product from $39$ . There are no more numbers to bring down, so we are done. The remainder is $3$ .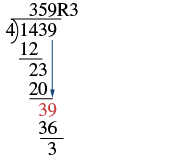
Check by multiplying.

So $1,439\div 4$ is $359$ with a remainder of $3$ . Our answer is correct.

[/hidden-answer]

try it

[ohm_question]144643[/ohm_question]

example

Divide and then check by multiplying: $1,461\div 13$ .
[reveal-answer q=”174689″]Show Answer[/reveal-answer]
[hidden-answer a=”174689″]

Solution

Let’s rewrite the problem to set it up for long division.	$13\overline{)1,461}$
First we try to divide $13$ into $1$ . Since that won’t work, we try $13$ into $14$ . There is $1$ thirteen in $14$ . We write the $1$ over the $4$ .
Multiply the $1$ by $13$ and subtract this product from $14$ .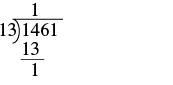
Now bring down the $6$ and repeat these steps. There is $1$ thirteen in $16$ . Write the $1$ over the $6$ . Multiply the $1$ by $13$ and subtract this product from $16$ .
Now bring down the $1$ and repeat these steps. There are $2$ thirteens in $31$ . Write the $2$ over the $1$ . Multiply the $2$ by $13$ and subtract this product from $31$ . There are no more numbers to bring down, so we are done. The remainder is $5$ . $1,462\div 13$ is $112$ with a remainder of $5$ .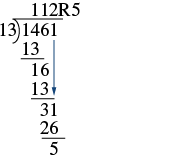
Check by multiplying.