1.16: Rounding Whole Numbers

Last updated
Save as PDF

Page ID: 45754

Lumen Learning
Lumen Learning

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Learning Objectives

Round whole numbers to a determined place value

Image of a Best Buy storefront with people walking along the sidewalk that runs in front of the entrance doors. — Best Buy Storefront

The electronics retailer, Best Buy, had $1,026$ brick and mortar stores open in October of $2016$. Depending on how this information will be used, it might be enough to say that the company has approximately one thousand stores. The word approximatelymeans that one thousand is not the exact count, but is close to the exact value.

In $2017$, the social network app, Facebook, reported its annual revenue as $40.7$ billion US dollars. This could mean they actually brought in $$40,742,985,316$ or $$40,654,872,131$. Sometimes the detail is needed, but sometimes just an approximate value is good enough. The real estate app, Zillow, recorded a profit of $1.07$ billion US dollars; this is an approximate value. If you want to compare Facebook’s $2017$ revenue with Zillow’s $2017$ revenue, the precise dollars or even millions of dollars are unnecessary.

The process of approximating a number is called rounding. Numbers are rounded to a specific place value depending on how much accuracy is needed. Identifying the number of stores owned by Best Buy as approximately $1$ thousand means we rounded to the thousands place. Reporting the annual revenue of Facebook as $40.7$ billion US dollars means we rounded to the hundred millions place. Often the place value to which we round depends on how we will need to use the number.

Using a number line can help us visualize and understand the rounding process. Look at the number line below.

Suppose we want to round the number $76$ to the nearest ten. Is $76$ closer to $70$ ($7$ tens) or $80$ ($8$ tens) on the number line?

We can see that $76$ is closer to $80$ than to $70$. So $76$ rounded to the nearest ten is $80$.

Now consider the number $72$. Find $72$ on the number line.

We can see that $72$ is closer to $70$, so $72$ rounded to the nearest ten is $70$.

How do we round $75$ to the nearest ten?

Find $75$ on the number line.

The number $75$ is exactly midway between $70$ and $80$.

So that everyone rounds the same way in cases like this, mathematicians have agreed to round up to the higher number. So, $75$ rounded to the nearest ten is $80$.

Now that we have looked at this process on the number line, we can introduce a more general procedure. To round a number to a specific place, look at the number to the right of that place. If the number is less than $5$, round down. If it is greater than or equal to $5$, round up.

So, for example, to round $76$ to the nearest ten, we look at the digit in the ones place.

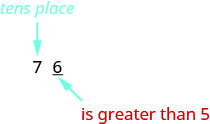
An image of value 76, with an arrow pointed at the seven with the label "tens place", and an arrow pointed at the six with the label "is greater than 5".
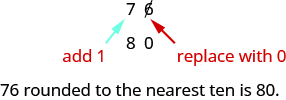
The digit in the ones place is a $6$. Because $6$ is greater than or equal to $5$, we increase the digit in the tens place by one. So the $7$ in the tens place becomes an $8$. Now, replace any digits to the right of the $8$ with zeros. So, $76$ rounds to $80$.

An image of the value 76 with six slashed through. An arrow points to the six with the label "replace with zero", and an arrow pointed to the seven with the label "add 1". Under the 76 is the number 80. The label says "76 rounded to the nearest ten is 80".
Let’s look again at rounding $72$ to the nearest $10$. Again, we look to the ones place.

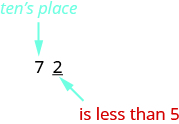
An image of value 72, with an arrow pointed at the seven with the label "tens place", and an arrow pointed at the two with the label "is less than 5".
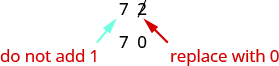
The digit in the ones place is $2$. Because $2$ is less than $5$, we keep the digit in the tens place the same and replace the digits to the right of it with zero. So $72$ rounded to the nearest ten is $70$.

An image of the value 72 with two slashed through. An arrow points to the two with the label "replace with zero", and an arrow pointed to the seven with the label "do not add 1". Under the 72 is the number 70.

Round a whole number to a specific place value

Locate the given place value. All digits to the left of that place value do not change.
Underline the digit to the right of the given place value.
Determine if this digit is greater than or equal to $5$.
- Yes—add $1$ to the digit in the given place value.
- No—do not change the digit in the given place value.
Replace all digits to the right of the given place value with zeros.

example

Round $843$ to the nearest ten.

Solution

Locate the tens place.
Underline the digit to the right of the tens place.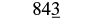
Since $3$ is less than $5$, do not change the digit in the tens place.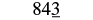
Replace all digits to the right of the tens place with zeros.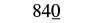
Rounding $843$ to the nearest ten gives $840$.

try it

[ohm_question hide_question_numbers=1]147151[/ohm_question]

Example

Round each number to the nearest hundred:

$23,658$
$3,978$

[reveal-answer q=”210558″]Show Answer[/reveal-answer]
[hidden-answer a=”210558″]

1.
Locate the hundreds place.
The digit of the right of the hundreds place is $5$. Underline the digit to the right of the hundreds place.
Since $5$ is greater than or equal to $5$, round up by adding $1$ to the digit in the hundreds place. Then replace all digits to the right of the hundreds place with zeros.	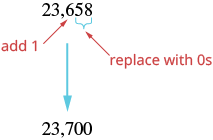So 23,658 rounded to the nearest hundred is 23,700.

2.
Locate the hundreds place.
Underline the digit to the right of the hundreds place.
The digit to the right of the hundreds place is $7$. Since $7$ is greater than or equal to $5$, round up by added $1$ to the $9$. Then place all digits to the right of the hundreds place with zeros.	So 3,978 rounded to the nearest hundred is 4,000.

[/hidden-answer]

try it

[ohm_question hide_question_numbers=1]147152[/ohm_question]

example

Round each number to the nearest thousand:

$147,032$
$29,504$

[reveal-answer q=”935310″]Show Answer[/reveal-answer]
[hidden-answer a=”935310″]

1.
Locate the thousands place. Underline the digit to the right of the thousands place.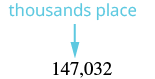
The digit to the right of the thousands place is $0$. Since $0$ is less than $5$, we do not change the digit in the thousands place.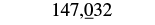
We then replace all digits to the right of the thousands pace with zeros.	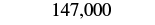So 147,032 rounded to the nearest thousand is 147,000.

2.
Locate the thousands place.
Underline the digit to the right of the thousands place.
The digit to the right of the thousands place is $5$. Since $5$ is greater than or equal to $5$, round up by adding $1$ to the $9$. Then replace all digits to the right of the thousands place with zeros.	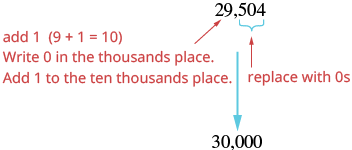So 29,504 rounded to the nearest thousand is 30,000.

Notice that in part 2, when we add $1$ thousand to the $9$ thousands, the total is $10$ thousands. We regroup this as $1$ ten thousand and $0$ thousands. We add the $1$ ten thousand to the $3$ ten thousands and put a $0$ in the thousands place.
[/hidden-answer]

try it

[ohm_question hide_question_numbers=1]143029[/ohm_question]

TRY IT

[ohm_question hide_question_numbers=1]143030[/ohm_question]

Watch the video below for more examples of how to round whole numbers to a given place value.

A YouTube element has been excluded from this version of the text. You can view it online here: http://pb.libretexts.org/afm-2/?p=50

Search

Text Color

Text Size

Margin Size

Font Type

Locate the tens place.
Underline the digit to the right of the tens place.
Since \(3\) is less than \(5\), do not change the digit in the tens place.
Replace all digits to the right of the tens place with zeros.
Rounding \(843\) to the nearest ten gives \(840\).

1.
Locate the hundreds place.
The digit of the right of the hundreds place is \(5\). Underline the digit to the right of the hundreds place.
Since \(5\) is greater than or equal to \(5\), round up by adding \(1\) to the digit in the hundreds place. Then replace all digits to the right of the hundreds place with zeros.	So 23,658 rounded to the nearest hundred is 23,700.