1.10: Percent Increase and Decrease

Last updated
Save as PDF

Page ID: 45769

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Learning Outcome

Solve problems involving percent increase and decrease

People in the media often talk about how much an amount has increased or decreased over a certain period of time — referring to politics, economics, demographics, etc. These statistical increases or decreases are usually expressed as a percent. In business, data is also often presented as percent change — analyzing profits, website traffic, customer satisfaction scores, etc.

Percent change refers to either percent increase or percent decrease depending on how the number has gained or lost value or magnitude.

Percent Increase

To find the percent increase, first we find the amount of increase, which is the difference between the new amount and the original amount. Then we find what percent the amount of increase is of the original amount.

Find Percent Increase

Step 1. Find the amount of increase.

increase = new amount − original amount

Step 2. Find the percent increase as a percent of the original amount.

example

In $2011$ , the California governor proposed raising community college fees from $\text{\$26}$ per unit to $\text{\$36}$ per unit. Find the percent increase. (Round to the nearest tenth of a percent.)

Solution

What are you asked to find?	the percent increase
Choose a variable to represent it.	Let $p=$ percent.
Find the amount of increase.
Find the percent increase.	The increase is what percent of the original amount?
Translate to an equation.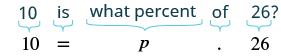
Divide both sides by $26$ .	${\Large\frac{10}{26}}={\Large\frac{26p}{26}}$
Round to the nearest thousandth.	$0.384=p$
Convert to percent form.	$\text{38.4%}=p$
Write a complete sentence.	The new fees represent a $38.4\text{%}$ increase over the old fees.

try it

[ohm_question]146704[/ohm_question]

[ohm_question]146705[/ohm_question]

Percent Decrease

Finding the percent decrease is very similar to finding the percent increase, but now the amount of decrease is the difference between the original amount and the final amount. Then we find what percent the amount of decrease is of the original amount.

Find percent decrease

Step 1. Find the amount of decrease.

decrease = original amount − new amount

Step 2. Find the percent decrease as a percent of the original amount.

example

The average price of a gallon of gas in one city in June $2014$ was $\text{\$3.71}$ . The average price in that city in July was $\text{\$3.64}$ . Find the percent decrease.
[reveal-answer q=”516647″]Show Answer[/reveal-answer]
[hidden-answer a=”516647″]

Solution

What are you asked to find?	the percent decrease
Choose a variable to represent it.	Let $p=$ percent.
Find the amount of decrease.
Find the percent of decrease.	The decrease is what percent of the original amount?
Translate to an equation.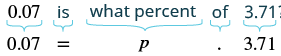
Divide both sides by $3.71$ .	${\Large\frac{0.07}{3.71}}={\Large\frac{3.71p}{3.71}}$
Round to the nearest thousandth.	$0.019=p$
Convert to percent form.	$\text{1.9%}=p$
Write a complete sentence.	The price of gas decreased $1.9\text{%}$ .