1.9: Solving Problems Using Percents

Last updated
Save as PDF

Page ID: 45768

Lumen Learning
Lumen Learning

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Learning Outcome

Evaluate expressions and word problems involving percents

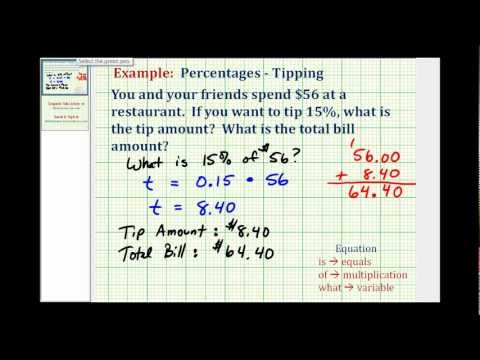
In this section we will solve percent questions by identifying the parts of the problem. We’ll look at a common application of percent—tips to a server at a restaurant—to see how to set up a basic percent application.

When Aolani and her friends ate dinner at a restaurant, the bill came to $\text{\$80}$. They wanted to leave a $20\%$ tip. What amount would the tip be?

To solve this, we want to find what amount is $20\%$ of $\$80$. The $\$80$ is called the base. The percent is the given $20\%$. The amount of the tip would be $0.20(80)$, or $\$16$ — see the image below. To find the amount of the tip, we multiplied the percent by the base.

A $20\%$ tip for an $\$80$ restaurant bill comes out to $\$16$.

Pieces of a Percent Problem

Percent problems involve three quantities: the base amount (the whole), the percent, and the amount (a part of the whole or partial amount).

The amount is a percent of the base.

Let’s look at another example:

Jeff has a Guitar Strings coupon for $15\%$ off any purchase of $$100$ or more. He wants to buy a used guitar that has a price tag of $$220$ on it. Jeff wonders how much money the coupon will take off the original $$220$ price. Problems involving percents will have some combination of these three quantities to work with: the percent, the amount, and the base. The percent has the percent symbol (%) or the word percent. In the problem above, $15\%$ is the percent off the purchase price. The base is the whole amount or original amount. In the problem above, the “whole” price of the guitar is $$220$, which is the base. The amount is the unknown and what we will need to calculate.

There are thee cases: a missing amount, a missing percent or a missing base. Let’s take a look at each possibility.

Solving for the Amount

When solving for the amount in a percent problem, you will multiply the percent (as a decimal or fraction) by the base. Typically we choose the decimal value for percent.

$\text{percent}\cdot{\text{base}}=\text{amount}$

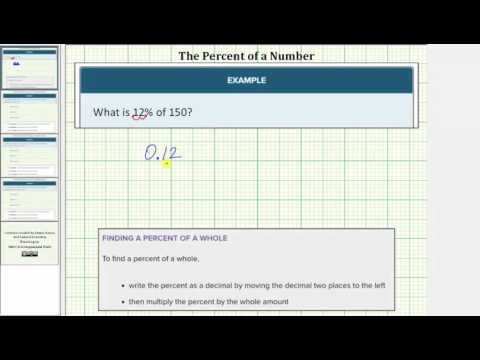
Example

Find $50\%$ of $20$

Solution:

First identify each piece of the problem:

percent: $50\%$ or $.5$

base: $20$

amount: unknown

Now plug them into your equation $\text{percent}\cdot{\text{base}}=\text{amount}$

$.5\cdot{20}= ?$

$.5\cdot{20}= 10$

Therefore, $10$ is the amount or part that is $50\%$ of $20$.

Example

What is $25\%$ of $80$?

[reveal-answer q=”813233″]Show Answer[/reveal-answer]
[hidden-answer a=”813233″]

The base is $80$ and the percent is $25\%$, so amount $= 80(0.25) = 20$

[/hidden-answer]

Try It

[ohm_question]80094[/ohm_question]

Thumbnail for the embedded element "Find the Percent of a Number"

A YouTube element has been excluded from this version of the text. You can view it online here: http://pb.libretexts.org/afm-2/?p=78

Solving for the Percent

When solving for the percent in a percent problem, you will divide the amount by the base. The equation above is rearranged and the percent will come back as a decimal of fraction you can report in the form asked of you.

$\Large{\frac{\text{amount}}{\text{base}}}\normalsize=\text{percent}$

Example

What percent of $320$ is $80$?

Solution:

First identify each piece of the problem:

percent: unknown

base: $320$

amount: $80$

Now plug the values into your equation $\Large{\frac{\text{amount}}{\text{base}}}\normalsize=\text{percent}$

$\large\frac{80}{320}\normalsize=?$

$\large\frac{80}{320}\normalsize=.25$

Therefore, $80$ is $25\%$ of $320$.

TRY IT

[ohm_question]80097[/ohm_question]

Thumbnail for the embedded element "Use the Percent Equation to Find a Percent"

A YouTube element has been excluded from this version of the text. You can view it online here: http://pb.libretexts.org/afm-2/?p=78

Solving for the Base

When solving for the base in a percent problem, you will divide the amount by the percent (as a decimal or fraction). The equation above is rearranged and you will find the base after plugging in the values.

$\Large{\frac{\text{amount}}{\text{percent}}}\normalsize=\text{base}$

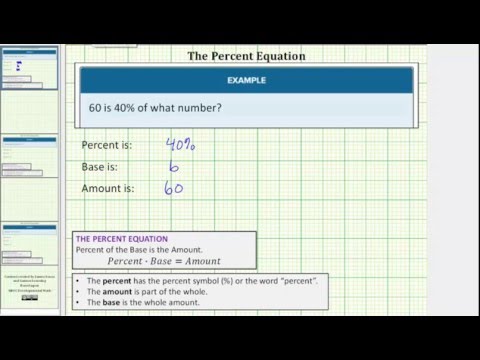
EXample

$60$ is $40\%$ of what number?

Solution:

First identify each piece of the problem:

percent:$40\%$ or $.4$

base: unknown

amount: $60$

Now plug the values into your equation $\Large{\frac{\text{amount}}{\text{percent}}}\normalsize=\text{base}$

$(60)\div(.4)=?$

$(60)\div(.4)=150$

Therefore, $60$ is $40\%$ of $150$.

Example

An article says that $15\%$ of a non-profit’s donations, about $$30,000$ a year, comes from individual donors. What is the total amount of donations the non-profit receives?

[reveal-answer q=”731314″]Show Answer[/reveal-answer]
[hidden-answer a=”731314″]

The percent is $15\%$, and $$30,000$ is the amount (or part of the whole). We are looking for the base.

base = $30000\div(.15)=$200000$

The non-profit receives $$200000$ a year in donations

[/hidden-answer]

TRY IT

[ohm_question]157022[/ohm_question]

Thumbnail for the embedded element "Use a Percent Equation to Solve for a Base or Whole Amount"

A YouTube element has been excluded from this version of the text. You can view it online here: http://pb.libretexts.org/afm-2/?p=78

Here are a few more percent problems for you to try.

try it

[ohm_question]146672[/ohm_question]

try it

[ohm_question]146692[/ohm_question]

try it

[ohm_question]146693[/ohm_question]

Many applications of percent occur in our daily lives, such as tips, sales tax, discount, and interest. To solve these applications we’ll translate to a basic percent equation, just like those we solved in the previous examples in this section. Once you translate the sentence into a percent equation, you know how to solve it.

example

Dezohn and his girlfriend enjoyed a dinner at a restaurant, and the bill was $\text{\$68.50}$. They want to leave an $\text{18%}$ tip. If the tip will be $\text{18%}$ of the total bill, how much should the tip be?

Solution

What are you asked to find?	the amount of the tip
What formula/equation should you use?	$\text{percent}\cdot{\text{base}}=\text{amount}$
Substitute in the correct values.	$(.18)\cdot{68.50}$
Solve.	$(.18)\cdot{68.50}=12.33$
Write a complete sentence that answers the question.	The couple should leave a tip of $\text{\$12.33}$.

try it

[ohm_question]146694[/ohm_question]

In the next video we show another example of finding how much tip to give based on percent.

Thumbnail for the embedded element "Percent Application - Tipping"

A YouTube element has been excluded from this version of the text. You can view it online here: http://pb.libretexts.org/afm-2/?p=78

example

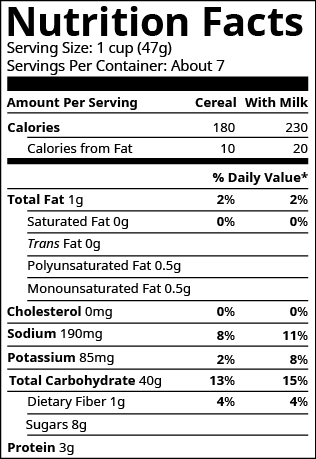
The label on Masao’s breakfast cereal said that one serving of cereal provides $85$ milligrams (mg) of potassium, which is $\text{2%}$ of the recommended daily amount. What is the total recommended daily amount of potassium?

The figures shows the nutrition facts for cereal.
[reveal-answer q=”744443″]Show Answer[/reveal-answer]
[hidden-answer a=”744443″]

Solution

What are you asked to find?	the total daily amount of potassium recommended (whole)
What formula/equation should you use?	$\Large{\frac{\text{amount}}{\text{percent}}}\normalsize=\text{base}$
Substitute in the correct values.	$\Large{\frac{85}{.02}}$
Solve.	$\Large{\frac{85}{.02}}\normalsize=4250$
Write a complete sentence that answers the question.	The amount of potassium that is recommended is $4,250$ mg.

[/hidden-answer]

try it

[ohm_question]146697[/ohm_question]

[ohm_question]146702[/ohm_question]

try it

[ohm_question]146703[/ohm_question]

Search

Text Color

Text Size

Margin Size

Font Type