1.4: Multiplying and Dividing Decimals
- Page ID
- 45763
Learning Objectives
- Use multiplication and division when evaluating expressions with decimals
Multiplying and dividing decimals can become complex, but we’re going to start with some basic multiplication by ten to warm-up.
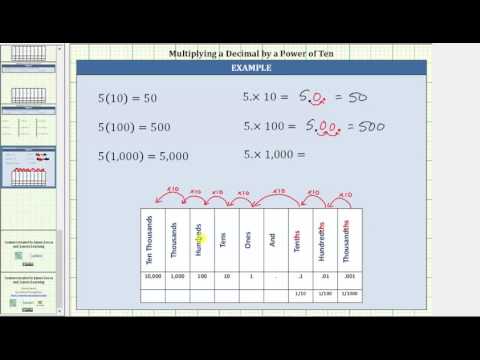
Multiply by Powers of 
In many fields, especially in the sciences, it is common to multiply decimals by powers of . Let’s see what happens when we multiply
by some powers of
.
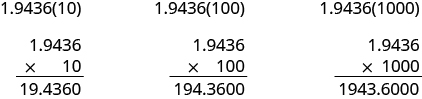
Look at the results without the final zeros. Do you notice a pattern?
The number of places that the decimal point moved is the same as the number of zeros in the power of ten. The table below summarizes the results.
| Multiply by | Number of zeros | Number of places decimal point moves |
|---|---|---|
We can use this pattern as a shortcut to multiply by powers of ten instead of multiplying using the vertical format. We can count the zeros in the power of and then move the decimal point that same of places to the right.
So, for example, to multiply by
, move the decimal point
places to the right.
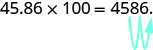
Sometimes when we need to move the decimal point, there are not enough decimal places. In that case, we use zeros as placeholders. For example, let’s multiply by
. We need to move the decimal point
places to the right. Since there is only one digit to the right of the decimal point, we must write a
in the hundredths place.
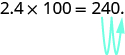
Multiply a decimal by a power of 
- Move the decimal point to the right the same number of places as the number of zeros in the power of
.
- Write zeros at the end of the number as placeholders if needed.
In the following video we show more examples of how to multiply a decimal by 10, 100, and 1000.
example
Multiply by factors of
1.
2.
3.
[reveal-answer q=”296737″]Show Answer[/reveal-answer]
[hidden-answer a=”296737″]
Solution
By looking at the number of zeros in the multiple of ten, we see the number of places we need to move the decimal to the right.
| 1. | |
| There is | 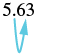 |
| 2. | |
| There are | 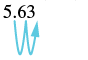 |
| 3. | |
| There are | 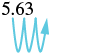 |
| A zero must be added at the end. |
[/hidden-answer]
TRY IT
[ohm_question]146599[/ohm_question]
Multiplying Decimals
Multiplying decimals is very much like multiplying whole numbers—we just have to determine where to place the decimal point. The procedure for multiplying decimals will make sense if we first review multiplying fractions.
Do you remember how to multiply fractions? To multiply fractions, you multiply the numerators and then multiply the denominators.
So let’s see what we would get as the product of decimals by converting them to fractions first. We will do two examples side-by-side below. Look for a pattern.
| A | B | |
|---|---|---|
| Convert to fractions. | ||
| Multiply. | ||
| Convert back to decimals. |
There is a pattern that we can use. In A, we multiplied two numbers that each had one decimal place, and the product had two decimal places. In B, we multiplied a number with one decimal place by a number with two decimal places, and the product had three decimal places.
How many decimal places would you expect for the product of If you said “five”, you recognized the pattern. When we multiply two numbers with decimals, we count all the decimal places in the factors—in this case two plus three—to get the number of decimal places in the product—in this case five.
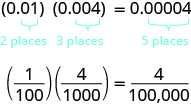
Once we know how to determine the number of digits after the decimal point, we can multiply decimal numbers without converting them to fractions first. The number of decimal places in the product is the sum of the number of decimal places in the factors. The rules for multiplying positive and negative numbers apply to decimals too.
Multiply decimal numbers
- Determine the sign of the product.
- Write the numbers in vertical format, lining up the numbers on the right.
- Multiply the numbers as if they were whole numbers, temporarily ignoring the decimal points.
- Place the decimal point. The number of decimal places in the product is the sum of the number of decimal places in the factors. If needed, use zeros as placeholders.
- Write the product with the appropriate sign.
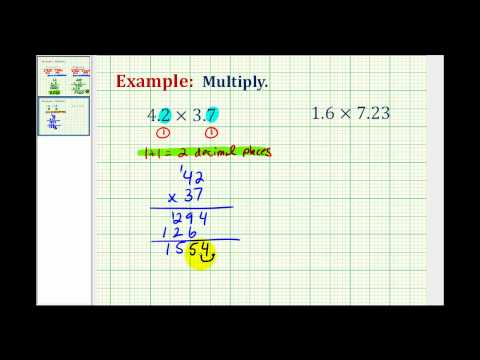
example
Multiply:
Solution
| Determine the sign of the product. The signs are the same. | The product will be positive. |
| Write the numbers in vertical format, lining up the numbers on the right. | 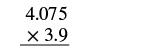 |
| Multiply the numbers as if they were whole numbers, temporarily ignoring the decimal points. | 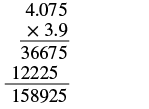 |
| Place the decimal point. Add the number of decimal places in the factors |  |
| The product is positive. |
try it
[ohm_question]146596[/ohm_question]
In the following video we show another example of how to multiply two decimals.
Dividing Decimals
Just as with multiplication, division of decimals is very much like dividing whole numbers — we have to figure out where the decimal point must be placed.
To understand decimal division, let’s consider the multiplication problem
Remember, a multiplication problem can be rephrased as a division problem. So we can write
We can think of this as “If we divide 8 tenths into four groups, how many are in each group?” The number line below shows that there are four groups of two-tenths in eight-tenths. So .

Using long division notation, we would write
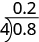
Notice that the decimal point in the quotient is directly above the decimal point in the dividend.
To divide a decimal by a whole number, we place the decimal point in the quotient above the decimal point in the dividend and then divide as usual. Sometimes we need to use extra zeros at the end of the dividend to keep dividing until there is no remainder.
Divide a decimal by a whole number
- Write as long division, placing the decimal point in the quotient above the decimal point in the dividend.
- Divide as usual.
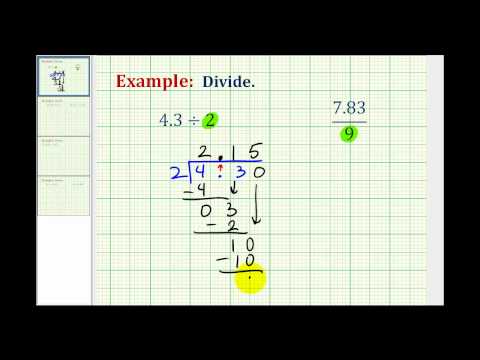
example
Divide:
Solution
| Write as long division, placing the decimal point in the quotient above the decimal point in the dividend. | 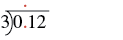 |
| Divide as usual. Since | 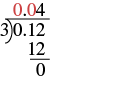 |
try it
[ohm_question]146600[/ohm_question]
Watch the following video to see another example of how to divide a decimal by a whole number.
Most commonly, this calculation will be done with money while shopping. Prices of products tend to be presented as a combination of dollars and cents (i.e. ,
, or
). You can then divide by the number of items or the number of units to determine the cost per item or unit.
example
Suppose a case of water bottles cost
. To find the price per water bottle, we would divide
by
, and round the answer to the nearest cent (hundredth).
Divide:
[reveal-answer q=”929706″]Show Answer[/reveal-answer]
[hidden-answer a=”929706″]
Solution
| Place the decimal point in the quotient above the decimal point in the dividend. | 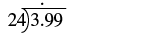 |
| Divide as usual. When do we stop? Since this division involves money, we round it to the nearest cent (hundredth). To do this, we must carry the division to the thousandths place. |  |
| Round to the nearest cent. | |
This means the price per bottle is cents.
[/hidden-answer]
try it
[ohm_question]145993[/ohm_question]
[ohm_question]156951[/ohm_question]
Next, we will divide a whole number by a decimal.
example
Divide:
[reveal-answer q=”616625″]Show Answer[/reveal-answer]
[hidden-answer a=”616625″]
Solution
| The signs are the same. | The quotient is positive. |
| Make the divisor a whole number by ‘moving’ the decimal point all the way to the right. Move the decimal point in the dividend the same number of places, adding zeros as needed. |  |
| Divide. Place the decimal point in the quotient above the decimal point in the dividend. | 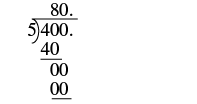 |
| Write the quotient with the appropriate sign. |
We can relate this example to money. How many nickels are there in four dollars? Because , there are
nickels in
.
[/hidden-answer]
try it
[ohm_question]146607[/ohm_question]
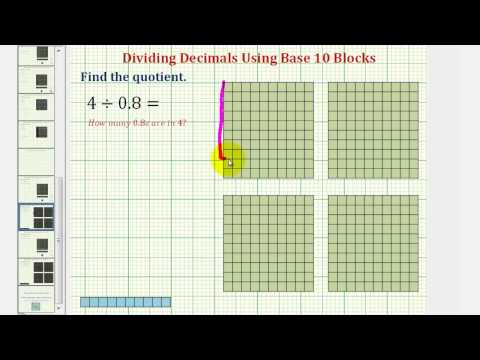
The following example shows how to divide a whole number by a decimal using base ten blocks.
- Prealgebra. Provided by: OpenStax. License: CC BY: Attribution. License Terms: Download for free at http://cnx.org/contents/caa57dab-41c...cda5519c@9.757