6.7: Decision Analysis and Monte Carlo Simulation for Investment Decisions

The earlier discussion in this chapter noted the effects of demand fluctuations but did not address uncertainty and contingencies. However, costs and demands are likely to be quite uncertain to forecast. Moreover, external events such as extreme events may also profoundly affect infrastructure costs, demand, and usage.

A common approach to dealing with uncertainty is to employ some form of ‘Monte Carlo’ simulation, where the name ‘Monte Carlo’ refers to a casino in Monaco with gambling on chance events. Monte Carlo simulation requires not only cash flow estimates in 98
each year, but also the probabilistic distributions of such cash flow as input information. As a result, there is considerably more work to prepare input (which is expensive and still uncertain) and to perform calculations (which fortunately is not very expensive with modern information technology).

The essential idea of Monte Carlo simulation is to obtain a sample from input parameter distributions and then assess the outcome from this sample. This process of sampling and assessment is repeated numerous times, resulting in a distribution of possible outcomes. So rather than a fixed, deterministic estimate of life cycle costs, Monte Carlo simulation results in a probability distribution of possible life cycle costs.

As an example, suppose you decided to do a Monte Carlo simulation of the life cycle roadway cost shown in Table 6.5.1 and Equation 6.5.2. The parameters in Table 6.5.1 might be used as input for a Monte Carlo roadway life cycle cost analysis with the following assumptions:

Table 6.7.1: Illustrative Input Parameter Distributions for a Roadway Life Cycle Cost.

Component	Year of Occurrence	Cost
Initial Construction	0	N(5,1)
First Rehabilitation	U[8,12]	N(2,2)
Second Rehabilitation	U[16,24]	N(1,1)
Maintenance	Each Year 1-30	U[0.05,0.15]

Monte Carlo Simulation (Note: \(N(\mu, \sigma)\) is normal distribution with mean \(\mu\) and standard deviation \(\sigma\), and \(U[i,u]\) is the uniform distribution with lower bound \(i\) and upper bound \(u\)).

The assumed parameter distributions are either normal or uniform with the mean equal to the values in Table 6.7.1. As a reminder, Figure 6.7.1 illustrates a normal distribution with different parameter values. To perform the Monte Carlo simulation, numerous samples (perhaps 500) would be drawn from the relevant distributions, each to form a single example case, and then Equation 6.5.2 applied to calculate life cycle costs for that case. The result would be numerous observations of possible life cycle costs.

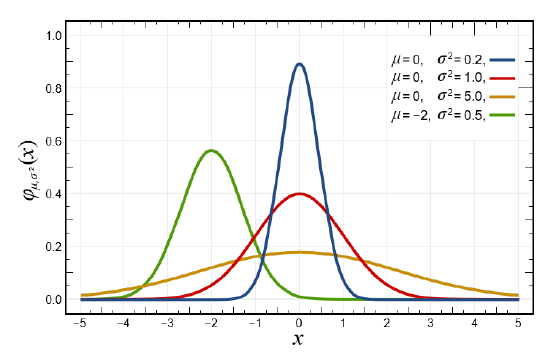
Figure \(\PageIndex{1}\): Illustration of Normal Distributions with Different Parameters. Source: By Inductiveload - self-made, Mathematica, Inkscape, Public Domain, via Wikimedia Commons https://commons.wikimedia.org/w/inde...?curid=3817954

Many software programs easily accommodate Monte Carlo simulation, including the Excel spreadsheet and Matlab. These software programs have regular functions or subprograms to generate random samples from input distributions. Monte Carlo simulations find use in a variety of application domains beyond infrastructure management, including environmental life cycle assessment and production planning. While Monte Carlo simulation explicitly considers uncertainty with stochastic inputs, it is crucially dependent upon the correctness of these input assumptions and modelling the effects of inputs. Accurately knowing the distributions of infrastructure costs and usage is unlikely. Users of Monte Carlo simulation should be aware of the classic computer adage: ‘garbage in, garbage out.’ Just because the results come from a complicated computer program, inaccurate inputs will not result in accurate results.

Another approach to exploring the effects of uncertainty is to use scenario and decision analysis. For our roadway cost example, scenario analysis might pertain to major underlying usage influences or natural disasters. For example, new industrial development in the roadway vicinity may result in much larger usage and faster pavement deterioration. As another example, major rehabilitation may be required in the case of earthquakes. Each of these situations may be a different scenario with different life cycle costs as a consequence. The scenarios might each have a Monte Carlo simulation analysis with different assumptions about input distributions.

Decision analysis would go further and include probabilities associated with different scenarios. Each scenario might also have different assumptions about future actions, such as a decision to widen the roadway in connection with a rehabilitation action. For this decision analysis approach, common applications would include both cost and benefit assessments to evaluate net present value effects.