6.6: Long Run Investment Decisions and Cost Functions
- Page ID
- 21143
It is possible to also develop long run cost functions in which the infrastructure itself may be changed to maximize net present value. In particular, rather than incur the high costs of congestion in high usage situations (as in Figure 6.3.1), an infrastructure manager might add capacity as rehabilitation investments are made.
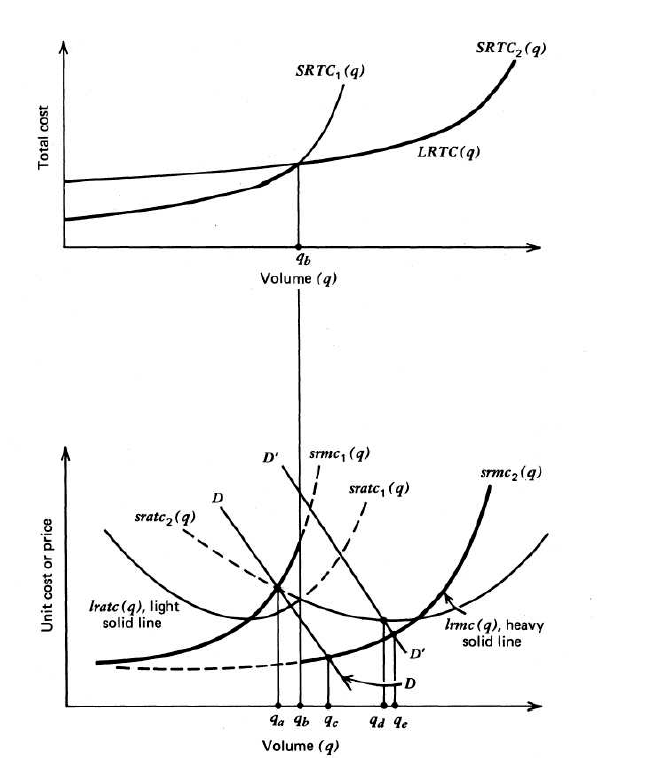
The long run total cost curve is the lower cost envelope of all possible short run total cost options. Figure 6.6.1 illustrates the situation in which two possible infrastructure capacity options exist (which might represent different size components, an additional floor on a parking garage or an additional lane of roadway capacity). There is a usage point (\(q_b\)) in Figure 6.6.1 at which it is desirable to shift from option 1 to the larger capacity option 2. The long run average total cost has a significant turn at this usage breakpoint, with scale economies beginning again! The long run marginal cost curve has a discontinuity at the breakpoint. With lower demand (demand curve \(D\)), the smaller option has lower costs, but with higher demand (demand curve \(D’\)), the larger option 2 is more desirable.