2.2: Quantification of Uncertainty via Probability Models
- Page ID
- 24473
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- In this section, you will learn how to quantify the relative frequency of occurrences of uncertain events by using probability models.
- You will learn about the measures of frequency, severity, likelihood, statistical distributions, and expected values.
- You will use examples to compute these values.
As we consider uncertainty, we use rigorous quantitative studies of chance, the recognition of its empirical regularity in uncertain situations. Many of these methods are used to quantify the occurrence of uncertain events that represent intellectual milestones. As we create models based upon probability and statistics, you will likely recognize that probability and statistics touch nearly every field of study today. As we have internalized the predictive regularity of repeated chance events, our entire worldview has changed. For example, we have convinced ourselves of the odds of getting heads in a coin flip so much that it’s hard to imagine otherwise. We’re used to seeing statements such as “average life of 1,000 hours” on a package of light bulbs. We understand such a phrase because we can think of the length of life of a light bulb as being uncertain but statistically predictable. We routinely hear such statements as “The chance of rain tomorrow is 20 percent.” It’s hard for us to imagine that only a few centuries ago people did not believe even in the existence of chance occurrences or random events or in accidents, much less explore any method of quantifying seemingly chance events. Up until very recently, people have believed that God controlled every minute detail of the universe. This belief rules out any kind of conceptualization of chance as a regular or predictable phenomenon. For example, until recently the cost of buying a life annuity that paid buyers $100 per month for life was the same for a thirty-year-old as it was for a seventy-year-old. It didn’t matter that empirically, the “life expectancy” of a thirty-year-old was four times longer than that of a seventy-year-old.The government of William III of England, for example, offered annuities of 14 percent regardless of whether the annuitant was 30 or 70 percent; (Karl Pearson, The History of Statistics In the 17th and 18th Centuries against the Changing Background of Intellectual, Scientific and Religious Thought (London: Charles Griffin & Co., 1978), 134. After all, people believed that a person’s particular time of death was “God’s will.” No one believed that the length of someone’s life could be judged or predicted statistically by any noticed or exhibited regularity across people. In spite of the advancements in mathematics and science since the beginning of civilization, remarkably, the development of measures of relative frequency of occurrence of uncertain events did not occur until the 1600s. This birth of the “modern” ideas of chance occurred when a problem was posed to mathematician Blaisé Pascal by a frequent gambler. As often occurs, the problem turned out to be less important in the long run than the solution developed to solve the problem.
The problem posed was: If two people are gambling and the game is interrupted and discontinued before either one of the two has won, what is a fair way to split the pot of money on the table? Clearly the person ahead at that time had a better chance of winning the game and should have gotten more. The player in the lead would receive the larger portion of the pot of money. However, the person losing could come from behind and win. It could happen and such a possibility should not be excluded. How should the pot be split fairly? Pascal formulated an approach to this problem and, in a series of letters with Pierre de Fermat, developed an approach to the problem that entailed writing down all possible outcomes that could possibly occur and then counting the number of times the first gambler won. The proportion of times that the first gambler won (calculated as the number of times the gambler won divided by the total number of possible outcomes) was taken to be the proportion of the pot that the first gambler could fairly claim. In the process of formulating this solution, Pascal and Fermat more generally developed a framework to quantify the relative frequency of uncertain outcomes, which is now known as probability. They created the mathematical notion of expected value of an uncertain event. They were the first to model the exhibited regularity of chance or uncertain events and apply it to solve a practical problem. In fact, their solution pointed to many other potential applications to problems in law, economics, and other fields.
From Pascal and Fermat’s work, it became clear that to manage future risks under uncertainty, we need to have some idea about not only the possible outcomes or states of the world but also how likely each outcome is to occur. We need a model, or in other words, a symbolic representation of the possible outcomes and their likelihoods or relative frequencies.
A Historical Prelude to the Quantification of Uncertainty Via Probabilities
Historically, the development of measures of chance (probability) only began in the mid-1600s. Why in the middle ages, and not with the Greeks? The answer, in part, is that the Greeks and their predecessors did not have the mathematical concepts. Nor, more importantly, did the Greeks have the psychological perspective to even contemplate these notions, much less develop them into a cogent theory capable of reproduction and expansion. First, the Greeks did not have the mathematical notational system necessary to contemplate a formal approach to risk. They lacked, for example, the simple and complete symbolic system including a zero and an equal sign useful for computation, a contribution that was subsequently developed by the Arabs and later adopted by the Western world. The use of Roman numerals might have been sufficient for counting, and perhaps sufficient for geometry, but certainly it was not conducive to complex calculations. The equal sign was not in common use until the late middle ages. Imagine doing calculations (even such simple computations as dividing fractions or solving an equation) in Roman numerals without an equal sign, a zero element, or a decimal point!
But mathematicians and scientists settled these impediments a thousand years before the advent of probability. Why did risk analysis not emerge with the advent of a more complete numbering system just as sophisticated calculations in astronomy, engineering, and physics did? The answer is more psychological than mathematical and goes to the heart of why we consider risk as both a psychological and a numerical concept in this book. To the Greeks (and to the millennia of others who followed them), the heavens, divinely created, were believed to be static and perfect and governed by regularity and rules of perfection—circles, spheres, the six perfect geometric solids, and so forth. The earthly sphere, on the other hand, was the source of imperfection and chaos. The Greeks accepted that they would find no sense in studying the chaotic events of Earth. The ancient Greeks found the path to truth in contemplating the perfection of the heavens and other perfect unspoiled or uncorrupted entities. Why would a god (or gods) powerful enough to know and create everything intentionally create a world using a less than perfect model? The Greeks, and others who followed, believed pure reasoning, not empirical, observation would lead to knowledge. Studying regularity in the chaotic earthly sphere was worst than a futile waste of time; it distracted attention from important contemplations actually likely to impart true knowledge.
It took a radical change in mindset to start to contemplate regularity in events in the earthly domain. We are all creatures of our age, and we could not pose the necessary questions to develop a theory of probability and risk until we shook off these shackles of the mind. Until the age of reason, when church reforms and a growing merchant class (who pragmatically examined and counted things empirically) created a tremendous growth in trade, we remained trapped in the old ways of thinking. As long as society was static and stationary, with villages this year being essentially the same as they were last year or a decade or century before, there was little need to pose or solve these problems. M. G. Kendall captures this succinctly when he noted that “mathematics never leads thought, but only expresses it.”* The western world was simply not yet ready to try to quantify risk or event likelihood (probability) or to contemplate uncertainty. If all things are believed to be governed by an omnipotent god, then regularity is not to be trusted, perhaps it can even be considered deceptive, and variation is irrelevant and illusive, being merely reflective of God’s will. Moreover, the fact that things like dice and drawing of lots were simultaneously used by magicians, by gamblers, and by religious figures for divination did not provide any impetus toward looking for regularity in earthly endeavors.
* M. G. Kendall, “The Beginnings of a Probability Calculus,” in Studies in the History of Statistics and Probability, vol. 1, ed. E. S. Pearson and Sir Maurice Kendall (London: Charles Griffin & Co., 1970), 30.
Measurement Techniques for Frequency, Severity, and Probability Distribution Measures for Quantifying Uncertain Events
When we can see the pattern of the losses and/or gains experienced in the past, we hope that the same pattern will continue in the future. In some cases, we want to be able to modify the past results in a logical way like inflating them for the time value of money discussed in "4: Evolving Risk Management - Fundamental Tools". If the patterns of gains and losses continue, our predictions of future losses or gains will be informative. Similarly, we may develop a pattern of losses based on theoretical or physical constructs (such as hurricane forecasting models based on physics or likelihood of obtaining a head in a flip of a coin based on theoretical models of equal likelihood of a head and a tail). Likelihood is the notion of how often a certain event will occur. Inaccuracies in our abilities to create a correct distribution arise from our inability to predict futures outcomes accurately. The distribution is the display of the events on a map that tells us the likelihood that the event or events will occur. In some ways, it resembles a picture of the likelihood and regularity of events that occur. Let’s now turn to creating models and measures of the outcomes and their frequency.
Measures of Frequency and Severity
Table 2.1 and Table 2.2 show the compilation of the number of claims and their dollar amounts for homes that were burnt during a five-year period in two different locations labeled Location A and Location B. We have information about the total number of claims per year and the amount of the fire losses in dollars for each year. Each location has the same number of homes (1,000 homes). Each location has a total of 51 claims for the five-year period, an average (or mean) of 10.2 claims per year, which is the frequency. The average dollar amount of losses per claim for the whole period is also the same for each location, $6,166.67, which is the definition of severity.
| Year | Number of Fire Claims | Number of Fire Losses ($) | Average Loss per Claim ($) |
|---|---|---|---|
| 1 | 11 | 16,500.00 | 1,500.00 |
| 2 | 9 | 40,000.00 | 4,444.44 |
| 3 | 7 | 30,000.00 | 4,285.71 |
| 4 | 10 | 123,000.00 | 12,300.00 |
| 5 | 14 | 105,000.00 | 7,500.00 |
| Total | 51.00 | 314,500.00 | 6,166.67 |
| Mean | 10.20 | 62,900.00 | 6,166.67 |
| Average Frequency = | 10.20 | ||
| Average Severity = | 6,166.67 for the 5-year period |
Table 2.2 Claims and Fire Losses ($) for Homes in Location B
| Year | Number of Fire Claims | Fire Losses | Average Loss per Claim ($) |
|---|---|---|---|
| 1 | 15 | 16,500.00 | 1,100.00 |
| 2 | 5 | 40,000.00 | 8,000.00 |
| 3 | 12 | 30,000.00 | 2,500.00 |
| 4 | 10 | 123,000.00 | 12,300.00 |
| 5 | 9 | 105,000.00 | 11,666.67 |
| Total | 51.00 | 314,500.00 | 6,166.67 |
| Mean | 10.20 | 62,900.00 | 6,166.67 |
| Average frequency = | 10.20 | ||
| Average severity = | 6,166.67 for the 5-year period |
As shown in Table 2.1 and Table 2.2, the total number of fire claims for the two locations A and B is the same, as is the total dollar amount of losses shown. You might recall from earlier, the number of claims per year is called the frequency. The average frequency of claims for locations A and B is 10.2 per year. The size of the loss in terms of dollars lost per claim is called severity, as we noted previously. The average dollars lost per claim per year in each location is $6,166.67.
The most important measures for risk managers when they address potential losses that arise from uncertainty are usually those associated with frequency and severity of losses during a specified period of time. The use of frequency and severity data is very important to both insurers and firm managers concerned with judging the risk of various endeavors. Risk managers try to employ activities (physical construction, backup systems, financial hedging, insurance, etc.) to decrease the frequency or severity (or both) of potential losses. In "4: Evolving Risk Management - Fundamental Tools", we will see frequency data and severity data represented. Typically, the risk manager will relate the number of incidents under investigation to a base, such as the number of employees if examining the frequency and severity of workplace injuries. In the examples in Table 2.1 and Table 2.2, the severity is related to the number of fire claims in the five-year period per 1,000 homes. It is important to note that in these tables the precise distribution (frequencies and dollar losses) over the years for the claims per year arising in Location A is different from distribution for Location B. This will be discussed later in this chapter. Next, we discuss the concept of frequency in terms of probability or likelihood.
Frequency and Probability
Returning back to the quantification of the notion of uncertainty, we first observe that our intuitive usage of the word probability can have two different meanings or forms as related to statements of uncertain outcomes. This is exemplified by two different statements:See Patrick Brockett and Arnold Levine Brockett, Statistics, Probability and Their Applications (W. B. Saunders Publishing Co., 1984), 62.
- “If I sail west from Europe, I have a 50 percent chance that I will fall off the edge of the earth.”
- “If I flip a coin, I have a 50 percent chance that it will land on heads.”
Conceptually, these represent two distinct types of probability statements. The first is a statement about probability as a degree of belief about whether an event will occur and how firmly this belief is held. The second is a statement about how often a head would be expected to show up in repeated flips of a coin. The important difference is that the first statement’s validity or truth will be stated. We can clear up the statement’s veracity for all by sailing across the globe.
The second statement, however, still remains unsettled. Even after the first coin flip, we still have a 50 percent chance that the next flip will result in a head. The second provides a different interpretation of “probability,” namely, as a relative frequency of occurrence in repeated trials. This relative frequency conceptualization of probability is most relevant for risk management. One wants to learn from past events about the likelihood of future occurrences. The discoverers of probability theory adopted the relative frequency approach to formalizing the likelihood of chance events.
Pascal and Fermat ushered in a major conceptual breakthrough: the concept that, in repeated games of chance (or in many other situations encountered in nature) involving uncertainty, fixed relative frequencies of occurrence of the individual possible outcomes arose. These relative frequencies were both stable over time and individuals could calculate them by simply counting the number of ways that the outcome could occur divided by the total number of equally likely possible outcomes. In addition, empirically the relative frequency of occurrence of events in a long sequence of repeated trials (e.g., repeated gambling games) corresponded with the theoretical calculation of the number of ways an event could occur divided by the total number of possible outcomes. This is the model of equally likely outcomes or relative frequency definition of probability. It was a very distinct departure from the previous conceptualization of uncertainty that had all events controlled by God with no humanly discernable pattern. In the Pascal-Fermat framework, prediction became a matter of counting that could be done by anyone. Probability and prediction had become a tool of the people! Figure \(\PageIndex{1}\) provides an example representing all possible outcomes in the throw of two colored dice along with their associated probabilities.
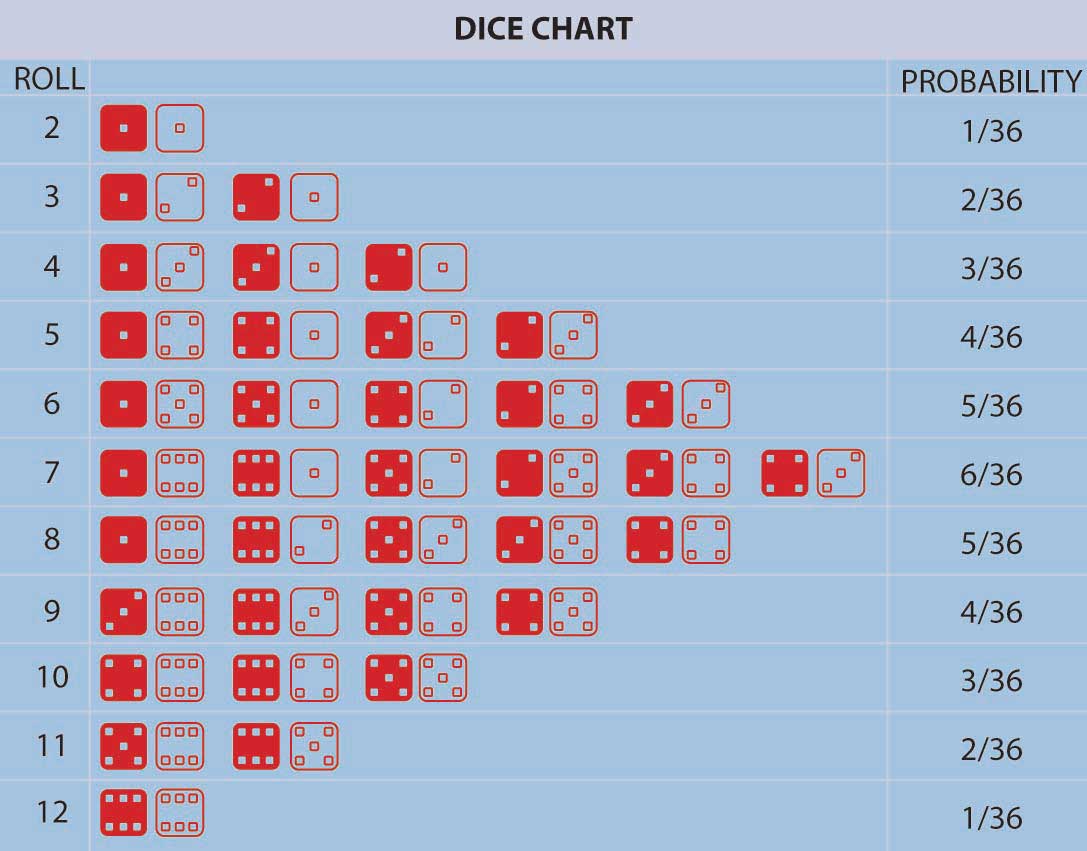
Figure \(\PageIndex{1}\) lists the probabilities for the number of dots facing upward (2, 3, 4, etc.) in a roll of two colored dice. We can calculate the probability for any one of these numbers (2, 3, 4, etc.) by adding up the number of outcomes (rolls of two dice) that result in this number of dots facing up divided by the total number of possibilities. For example, a roll of thirty-six possibilities total when we roll two dice (count them). The probability of rolling a 2 is 1/36 (we can only roll a 2 one way, namely, when both dice have a 1 facing up). The probability of rolling a 7 is \(\frac{6}{36}\)=\(\frac{1}{6}\) (since rolls can fall any of six ways to roll a 7—1 and 6 twice, 2 and 5 twice, 3 and 4 twice). For any other choice of number of dots facing upward, we can get the probability by just adding the number of ways the event can occur divided by thirty-six. The probability of rolling a 7 or an 11 (5 and 6 twice) on a throw of the dice, for instance, is \(\frac{6+2}{36}\)=\(\frac{2}{9}\).
The notions of “equally likely outcomes” and the calculation of probabilities as the ratio of “the number of ways in which an event could occur, divided by the total number of equally likely outcomes” is seminal and instructive. But, it did not include situations in which the number of possible outcomes was (at least conceptually) unbounded or infinite or not equally likely.Nor was the logic of the notion of equally likely outcomes readily understood at the time. For example, the famous mathematician D’Alembert made the following mistake when calculating the probability of a head appearing in two flips of a coin (Karl Pearson, The History of Statistics in the 17th and 18th Centuries against the Changing Background of Intellectual, Scientific and Religious Thought [London: Charles Griffin & Co., 1978], 552). D’Alembert said the head could come up on the first flip, which would settle that matter, or a tail could come up on the first flip followed by either a head or a tail on the second flip. There are three outcomes, two of which have a head, and so he claimed the likelihood of getting a head in two flips is \(\frac{2}{3}\). Evidently, he did not take the time to actually flip coins to see that the probability was \(\frac{3}{4}\), since the possible equally likely outcomes are actually (H,T), (H,H), (T,H), (T,T) with three pairs of flips resulting in a head. The error is that the outcomes stated in D’Alembert’s solution are not equally likely using his outcomes H, (T,H), (T,T), so his denominator is wrong. The moral of this story is that postulated theoretical models should always be tested against empirical data whenever possible to uncover any possible errors. We needed an extension. Noticing that the probability of an event, any event, provided that extension. Further, extending the theory to nonequally likely possible outcomes arose by noticing that the probability of an event—any event—occurring could be calculated as the relative frequency of an event occurring in a long run of trials in which the event may or may not occur. Thus, different events could have different, nonequal chances of occurring in a long repetition of scenarios involving the possible occurrences of the events. Table 2.3 provides an example of this. We can extend the theory yet further to a situation in which the number of possible outcomes is potentially infinite. But what about a situation in which no easily definable bound on the number of possible outcomes can be found? We can address this situation by again using the relative frequency interpretation of probability as well. When we have a continuum of possible outcomes (e.g., if an outcome is time, we can view it as a continuous variable outcome), then a curve of relative frequency is created. Thus, the probability of an outcome falling between two numbers x and y is the area under the frequency curve between x and y. The total area under the curve is one reflecting that it’s 100 percent certain that some outcome will occur.
The so-called normal distribution or bell-shaped curve from statistics provides us with an example of such a continuous probability distribution curve. The bell-shaped curve represents a situation wherein a continuum of possible outcomes arises. Figure \(\PageIndex{2}\) provides such a bell-shaped curve for the profitability of implementing a new research and development project. It may have profit or loss.
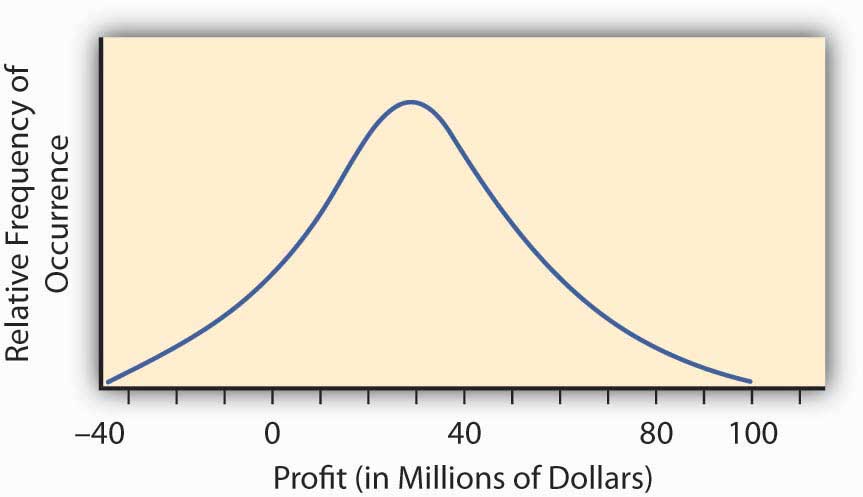
To find the probability of any range of profitability values for this research and development project, we find the area under the curve in Figure \(\PageIndex{2}\) between the desired range of profitability values. For example, the distribution in Figure \(\PageIndex{2}\) was constructed to have what is called a normal distribution with the hump over the point $30 million and a measure of spread of $23 million. This spread represents the standard deviation that we will discuss in the next section. We can calculate the area under the curve above $0, which will be the probability that we will make a profit by implementing the research and development project. We do this by reference to a normal distribution table of values available in any statistics book. The area under the curve is 0.904, meaning that we have approximately a 90 percent change (probability of 0.9) that the project will result in a profit.
In practice, we build probability distribution tables or probability curves such as those in Figure \(\PageIndex{1}\), Figure \(\PageIndex{2}\), and Table 2.3 using estimates of the likelihood (probability) of various different states of nature based on either historical relative frequency of occurrence or theoretical data. For example, empirical data may come from repeated observations in similar situations such as with historically constructed life or mortality tables. Theoretical data may come from a physics or engineering assessment of failure likelihood for a bridge or nuclear power plant containment vessel. In some situations, however, we can determine the likelihoods subjectively or by expert opinion. For example, assessments of political overthrows of governments are used for pricing political risk insurance needed by corporations doing business in emerging markets. Regardless of the source of the likelihoods, we can obtain an assessment of the probabilities or relative frequencies of the future occurrence of each conceivable event. The resulting collection of possible events together with their respective probabilities of occurrence is called a probability distribution, an example of which is shown in Table 2.3.
Measures of Outcome Value: Severity of Loss, Value of Gain
We have developed a quantified measure of the likelihood of the various uncertain outcomes that a firm or individual might face—these are also called probabilities. We can now turn to address the consequences of the uncertainty. The consequences of uncertainty are most often a vital issue financially. The reason that uncertainty is unsettling is not the uncertainty itself but rather the various different outcomes that can impact strategic plans, profitability, quality of life, and other important aspects of our life or the viability of a company. Therefore, we need to assess how we are impacted in each state of the world. For each outcome, we associate a value reflecting how we are affected by being in this state of the world.
As an example, consider a retail firm entering a new market with a newly created product. They may make a lot of money by taking advantage of “first-mover” status. They may lose money if the product is not accepted sufficiently by the marketplace. In addition, although they have tried to anticipate any problems, they may be faced with potential product liability. While they naturally try to make their products as safe as possible, they have to regard the potential liability because of the limited experience with the product. They may be able to assess the likelihood of a lawsuit as well as the consequences (losses) that might result from having to defend such lawsuits. The uncertainty of the consequences makes this endeavor risky and the potential for gain that motivates the company’s entry into the new market. How does one calculate these gains and losses? We already demonstrated some calculations in the examples above in Table 2.1 and Table 2.2 for the claims and fire losses for homes in locations A and B. These examples concentrated on the consequences of the uncertainty about fires. Another way to compute the same type of consequences is provided in the example in Table 2.3 for the probability distribution for this new market entry. We look for an assessment of the financial consequences of the entry into the market as well. This example looks at a few possible outcomes, not only the fire losses outcome. These outcomes can have positive or negative consequences. Therefore, we use the opportunity terminology here rather than only the loss possibilities.
| State of Nature | Probability Assessment of Likelihood of State | Financial Consequences of Being in This State (in Millions of Dollars) |
|---|---|---|
| Subject to a loss in a product liability lawsuit | .01 | −10.2 |
| Market acceptance is limited and temporary | .10 | −.50 |
| Some market acceptance but no great consumer demand | .40 | .10 |
| Good market acceptance and sales performance | .40 | 1 |
| Great market demand and sales performance | .09 | 8 |
As you can see, it’s not the uncertainty of the states themselves that causes decision makers to ponder the advisability of market entry of a new product. It’s the consequences of the different outcomes that cause deliberation. The firm could lose $10.2 million or gain $8 million. If we knew which state would materialize, the decision would be simple. We address the issue of how we combine the probability assessment with the value of the gain or loss for the purpose of assessing the risk (consequences of uncertainty) in the next section.
Combining Probability and Outcome Value Together to Get an Overall Assessment of the Impact of an Uncertain Endeavor
Early probability developers asked how we could combine the various probabilities and outcome values together to obtain a single number reflecting the “value” of the multitude of different outcomes and different consequences of these outcomes. They wanted a single number that summarized in some way the entire probability distribution. In the context of the gambling games of the time when the outcomes were the amount you won in each potential uncertain state of the world, they asserted that this value was the “fair value” of the gamble. We define fair value as the numerical average of the experience of all possible outcomes if you played the game over and over. This is also called the “expected value.” Expected value is calculated by multiplying each probability (or relative frequency) by its respective gain or loss.In some ways it is a shame that the term “expected value” has been used to describe this concept. A better term is “long run average value” or “mean value” since this particular value is really not to be expected in any real sense and may not even be a possibility to occur (e.g., the value calculated from Table 2.3 is 1.008, which is not even a possibility). Nevertheless, we are stuck with this terminology, and it does convey some conception of what we mean as long as we interpreted it as being the number expected as an average value in a long series of repetitions of the scenario being evaluated. It is also referred to as the mean value, or the average value. If X denotes the value that results in an uncertain situation, then the expected value (or average value or mean value) is often denoted by \(E(X)\), sometimes also referred to by economists as \(E(U)\)—expected utility—and \(E(G)\)—expected gain. In the long run, the total experienced loss or gain divided by the number of repeated trials would be the sum of the probabilities times the experience in each state. In Table 2.3 the expected value is \((.01)×(–10.2) + (.1) ×( −.50) + (.4) ×(.1) + (.4) ×(1) + (.09) ×(8) = 1.008\). Thus, we would say the expected outcome of the uncertain situation described in Table 2.3 was $1.008 million, or $1,008,000.00. Similarly, the expected value of the number of points on the toss of a pair of dice calculated from example in Figure \(\PageIndex{1}\) is \(2×((\frac{1}{36})+3×(\frac{2}{36})+4 ×(\frac{3}{36})+5×(\frac{4}{36})+6×(\frac{5}{36})+7×(\frac{6}{36})+8×(\frac{5}{36})+9×(\frac{4}{36})+10×(\frac{3}{36})+11×(\frac{2}{36})+12×(\frac{1}{36})= 7\). In uncertain economic situations involving possible financial gains or losses, the mean value or average value or expected value is often used to express the expected returns.Other commonly used measures of profitability in an uncertain opportunity, other than the mean or expected value, are the mode (the most likely value) and the median (the number with half the numbers above it and half the numbers below it—the 50 percent mark). It represents the expected return from an endeavor; however, it does not express the risk involved in the uncertain scenario. We turn to this now.
Relating back to Table 2.1 and Table 2.2, for locations A and B of fire claim losses, the expected value of losses is the severity of fire claims, $6,166.67, and the expected number of claims is the frequency of occurrence, 10.2 claims per year.
Key Takeaways
In this section you learned about the quantification of uncertain outcomes via probability models. More specifically, you delved into methods of computing:
- Severity as a measure of the consequence of uncertainty—it is the expected value or average value of the loss that arises in different states of the world. Severity can be obtained by adding all the loss values in a sample and dividing by the total sample size.
- If we take a table of probabilities (probability distribution), the expected value is obtained by multiplying the probability of a particular loss occurring times the size of the loss and summing over all possibilities.
- Frequency is the expected number of occurrences of the loss that arises in different states of the world.
- Likelihood and probability distribution represent relative frequency of occurrence (frequency of occurrence of the event divided by the total frequency of all events) of different events in uncertain situations.
Discussion Questions
- A study of data losses incurred by companies due to hackers
penetrating the Internet security of the firm found that 60 percent
of the firms in the industry studied had experienced security
breaches and that the average loss per security breach was
$15,000.
- What is the probability that a firm will not have a security breach?
- One firm had two breaches in one year and is contemplating spending money to decrease the likelihood of a breach. Assuming that the next year would be the same as this year in terms of security breaches, how much should the firm be willing to pay to eliminate security breaches (i.e., what is the expected value of their loss)?
- The following is the experience of Insurer A for the last three
years:
Year Number of Exposures Number of Collision Claims Collision Losses ($) 1 10,000 375 350,000 2 10,000 330 250,000 3 10,000 420 400,000 - What is the frequency of losses in year 1?
- Calculate the probability of a loss in year 1.
- Calculate the mean losses per year for the collision claims and losses.
- Calculate the mean losses per exposure.
- Calculate the mean losses per claim.
- What is the frequency of the losses?
- What is the severity of the losses?
- The following is the experience of Insurer B for the last three
years:
Year Number of Exposures Number of Collision Claims Collision Losses ($) 1 20,000 975 650,000 2 20,000 730 850,000 3 20,000 820 900,000 - Calculate the mean or average number of claims per year for the insurer over the three-year period.
- Calculate the mean or average dollar value of collision losses per exposure for year 2.
- Calculate the expected value (mean or average) of losses per claim over the three-year period.
- For each of the three years, calculate the probability that an exposure unit will file a claim.
- What is the average frequency of losses?
- What is the average severity of the losses?
- What is the standard deviation of the losses?
- Calculate the coefficient of variation.


