18: Leases
- Page ID
- 12763
After completing this chapter, you should be able to: (1) understand how leasing can provide an alternative method for gaining control of and access to capital resources; and (2) evaluate leases using present value (PV) models developed earlier.
To achieve your learning goals, you should complete the following objectives:
- Learn how leasing arrangements offer a different method for gaining control of and access to capital resources.
- Distinguish between the different forms of leases including the sale and leaseback lease, the operating lease, and the financial or capital lease.
- Learn the differences between leases and rental agreements.
- Learn how lease agreements are taxed.
- Learn the advantages and disadvantages of entering a lease agreement versus owning a capital resource.
- Learn how to find the break-even purchase price when compared to a leasing option.
Introduction
Control of a durable can be transferred between parties in several ways. A lease agreement is one important way. A lease is a contract through which control over the right to use a durable is transferred from one party, the lessor, to another party, the lessee who acquires control of the durable. In exchange for the right to use or control a durable for a specified time period, the lessee pays the lessor a rental payment or share in the output produced by the leased durable. The lease payment or shared output must cover the opportunity cost of funds invested in the leased item, depreciation of the durable, and other incidental ownership costs incurred by the lessor. Thus, leasing is a method of financing the control of a durable that separates its use from its ownership.
There are several kinds of lease arrangements and several kinds of durables that are leased. Farmland is frequently leased as are machines, houses, cars, computers, coping equipment, buildings, breeding livestock, and many kinds of management services. In this chapter, we describe various types of leases, evaluate their advantages and disadvantages, and apply present value (PV) tools to analyze leasing benefits for both the lessor and the lessee.
Types of Lease Agreements
Sale and leaseback. Under the sale-and-leaseback agreement, a firm owning a durable to be leased sells the durable to a financial institution and simultaneously executes an agreement to lease the durable back. Thus, the lease becomes the alternative to a purchase with a specific advantage to the lessee: namely, he or she is allowed to write off the entire lease payment as an expense instead of just interest costs and depreciation. The lessor will not enter into this type of lease agreement unless the lease payments are sufficient to return the full purchase price plus a return on the investment to the lessor.
Operating leases. Operating leases, sometimes called service leases, provide for both financing and maintenance. These leases ordinarily call for the lessor to maintain the leased equipment. The cost of the maintenance is built into the lease payment. Computers and office copiers, together with cars and trucks, are the primary types of equipment involved in operating leases.
In the case of operating leases, lease payments are often insufficient to recover the full cost of the equipment. To offset this feature, the lease is written for a time period considerably less than the expected life of the leased equipment, leaving the lessor to recover his or her investment in renewal payments of the lease or through disposal of the leased equipment.
One of the main advantages of the operating lease for lessees is the cancellation of the short lease period which allows them to adopt and bring into use more advanced equipment. Thus, for durables subject to rapid changes in technology, an operating lease is often a preferred method for gaining control of a durable.
Financial or capital leases. A financial lease is a fully amortized lease whose PV of the lease payments equals the full price of the leased equipment. It does not provide for maintenance service nor may it be canceled. The financial lease begins with a lessee selecting the specific items it requires and agreeing with the lessor about the price and the delivery of the item. The lessor arranges with a bank or another financial institution to purchase the equipment and simultaneously executes a financial lease with the lessee intending to use the equipment. The purchase of the equipment builds into the lease payments a rate of return equivalent to what would be charged on a loan, and the lease is canceled when the purchase price of the durable plus a return for the lessor is paid.
Under financial leases, lessees generally pay property taxes and insurance and, in many cases, can acquire ownership of the durable at the end of the lease. The significant difference between the sale-and-leaseback lease and the financial lease is that the lessee purchases the durable directly from the manufacturer rather than from the lessor under the terms of the financial lease.
Lease Agreements and Taxes
One of the major effects of the lease is to alter the tax obligations of the lessee and lessor. Therefore, special attention is required to make sure that lease agreements are acceptable under current tax codes as interpreted in the United States by the Internal Revenue Service. There is an important distinction between a lease agreement and a loan for tax purposes. If the lease agreement cannot be distinguished from an ordinary loan agreement, then any special tax provisions associated with the lease agreement are lost.
To distinguish a lease from a sale agreement, the term over which the investment durable is leased must be less than 75 percent of the economic life of the durable. Nor should the lessee be granted any special repurchase option not available to others not involved in the lease. There are other conditions as well; tax codes are evolving documents that are constantly being updated.
Lease Liquidity and Risk
Normally, the decision to acquire the durable is not at issue in the typical lease analysis. The issue at hand is whether to acquire control of the durable through a lease or by purchasing it—often by borrowing funds to finance the purchase. The decision requires a careful examination of the advantages of leasing. Leasing offers several possible advantages relative to owning a durable that we describe next.
Release of cash and credit. When a firm leases or sells a durable on a leaseback arrangement, the lessee avoids the cash down payment required to purchase the investment. More generally, the liquidity of a lease versus the liquidity of a purchase depends on which option requires the most accelerated payments.
Some texts discuss in detail the effect on the firm’s credit reserve as a result of leasing. If leasing uses up credit at a slower rate than borrowing, there may be credit incentives for leasing rather than borrowing. However, lenders are likely to recognize that long-term lease agreements place the same requirements on the firm’s future cash flow as loans do.
Obsolescence risk. Investments may experience significant obsolescence risks. In addition, there is some risk that the need for durables’ services will change before the durables’ service capacity is exhausted. Part of this obsolescence and use risk may be reduced through a lease arrangement for a short time period, especially if the lessor is less subject to obsolescence risk than the lessee. This is likely the case where the leased equipment has alternative uses in other firms or industries and where the risk can be spread over many lessees.
Idle capacity risk. Another risk that can often be reduced through lease arrangement is the risk of holding idle equipment. If the demand for services from a durable is not sufficient to employ the durable full time, the lessee can reduce idle capacity risk by leasing rather than owning the durable. From the lessor’s point of view, the durable can be completely employed because many lessees will use the equipment.
Foreclosure risk. In many respects, leasing is similar to borrowing because it represents an obligation of the firm to a series of future cash payments. There is one significant difference between agreeing to lease and borrowing to purchase the durable. In the case of financial difficulties, the lessor simply takes back the equipment because he or she holds the legal title. In the case of a loan, inability to meet loan payments may result in more complex foreclosure proceedings.
Tax advantages. A tax advantage may be gained when the term of the lease is shorter than the allowable tax depreciation period for ownership. However, tax incentives for the lessee must be a result of a lower total tax burden for the lessee and lessor. This situation implies that the lease arrangement has legitimately allowed for a reduction in the total amount of taxes paid. Needless to say, the Internal Revenue Service imposes conditions on what does and does not constitute a legal lease.
Net Present Cost of Leasing versus Purchasing
The decision to lease or to buy a durable depends on the net present cost (NPC) of leasing versus NPC of purchasing the durable. Since the size and timing of the cash flow, influence of taxes, and risks associated with buying and leasing are different, they represent two different investment opportunities which are amenable to analysis using PV models. In the following discussion, the after-tax cash flow is considered risk-adjusted, and the problem is treated as riskless.
To compare the lease with the purchase option, the firm considers itself in both roles—that of a lessee and lessor—and finds the maximum lease payment it could pay and be indifferent between purchasing or leasing the durable. We begin by describing the NPC of the lease (NPCL). Because we are describing the NPC of the lease, cash costs are treated as positive flow, and income that reduces the cost of leasing is treated as negative cash flow. For simplicity, we will assume a maximum constant lease payment equal to C. Then we assume the lease payment at age t is Ct, the lessee’s constant marginal tax rate is T, the lessee’s before-tax opportunity cost of capital is r, and the lessee’s tax adjustment coefficient is θ as described in Chapter 11. With these definitions in place, the net present cost of a lease for n periods, NPCL, can be expressed as:
\[-N P C^{L}=C(1-T)+\frac{C(1-T)}{[1-r(1-\theta T)]}+\cdots+\frac{C(1-T)}{[1-r(1-\theta T)]^{n-1}} \label{18.1}\]
Notice in Equation \ref{18.1} that the first
lease payment is made at the beginning of the lease payment rather
than at the end of the lease period, which would be the case of a
loan. Therefore, leases can be viewed as an annuity due type of
financial arrangement. Multiplying both sides of Equation
\ref{18.1} by 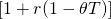 and summing the resulting geometric series, we write the result
as:
and summing the resulting geometric series, we write the result
as:
\[N P C^{L}=C(1-T)\left\{1+U S_{0}[r(1-\theta T), n-1]\right\} \label{18.2}\]
where:
\[U S_{0}[r(1-\theta T), n-1]=\frac{C(1-T)}{[1-r(1-\theta T)]}+\cdots+\frac{C(1-T)}{[1-r(1-\theta T)]^{n-1}} \label{18.3}\]
We now consider the net present cost of a cash
purchase, NPCP, for the same financial manager who
previously considered the lease option. We begin by assuming that
the market value of the durable leased or purchased is equal to
V0. We also assume that 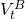 is the book value of the depreciable durable at age t. We continue
to assume that the purchaser’s opportunity cost of capital is
r, the average tax rate is T, and
is the book value of the depreciable durable at age t. We continue
to assume that the purchaser’s opportunity cost of capital is
r, the average tax rate is T, and 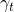 is the percentage of the investment’s value allowed to be deducted
in year t where t = 1, …, n, and the tax
adjustment coefficient is
is the percentage of the investment’s value allowed to be deducted
in year t where t = 1, …, n, and the tax
adjustment coefficient is 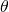 .
Of course, the sum of the amount deducted cannot exceed the value
of the investment so that
.
Of course, the sum of the amount deducted cannot exceed the value
of the investment so that 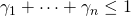 .
All these assumptions allow us to write the NPCP as:
.
All these assumptions allow us to write the NPCP as:
\[\begin{align} N P C^{P}=V_{0}-\frac{T \gamma_{1} V_{0}}{[1+r(1-\theta T)]}-\cdots \\[4pt] -\frac{T \gamma_{n} V_{0}}{[1+r(1-\theta T)]^{n}}-\frac{V_{n}-T \gamma_{n} V_{n}}{[1+r(1-\theta T)]^{n}} \label{18.4} \end{align}\]
The purchaser’s cost on the right-hand side of
Equation \ref{18.4} is the purchase price V0,
less n periods of tax savings from depreciation equal to
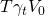 in the period discounted to the present period. The liquidation
value Vn minus a tax adjustment term
in the period discounted to the present period. The liquidation
value Vn minus a tax adjustment term 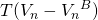 reduces the purchaser’s cost. The adjustment term accounts for the
tax consequences of a difference between the liquidation value and
the book value of the investment. If the investment is completely
depreciated by the nth period, and the
liquidation value is zero, then the NPCP can be written
as:
reduces the purchaser’s cost. The adjustment term accounts for the
tax consequences of a difference between the liquidation value and
the book value of the investment. If the investment is completely
depreciated by the nth period, and the
liquidation value is zero, then the NPCP can be written
as:
\[N P C^{P}=V_{0}-\frac{T \gamma_{1} V_{0}}{[1+r(1-\theta T)]}-\cdots-\frac{T \gamma_{n} V_{0}}{[1+r(1-\theta T)]^{n}} \label{18.5}\]
Finally, if the NPCL, expressed as the right-hand side of Equation \ref{18.2}, is equated to NPCP, expressed as the left-hand side of Equation \ref{18.5}, we can solve for the lease payment C, a maximum bid lease, which equates the two alternatives for controlling the services from the durable.
\[C=\frac{N P C^{p}}{(1-T)\left\{1+U S_{0}[r(1-\theta T), n-1]\right\}} \label{18.6}\]
Consider an example. Go Green is a lawn service
that requires a new truck to service its customers. It wants to
know the largest lease payment it could afford and still be as well
off as it would be if it purchased the truck. The truck in question
has a new sticker price of $30,000 and can be depreciated using a
straight-line method over five years. At the end of the lease, the
truck has a liquidation value of $5,000. To find the maximum bid
payment, the following assumptions are used: T = 32%,
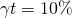 for t = 1, …, 5, r = 14%,
for t = 1, …, 5, r = 14%, 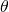 = 1, n = 5, Vn = $5,000, and
= 1, n = 5, Vn = $5,000, and 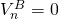 .
Finally, the after-tax discount rate is r(1 – T)
= .14(1 – .32) = .095
.
Finally, the after-tax discount rate is r(1 – T)
= .14(1 – .32) = .095
To find the maximum bid payment, we first find NPCP by substituting numerical values into Equation \ref{18.6}:
\[N P C^{P}=\$ 30,000-(.32)(\$ 6,000) U S_{0}(0.095,5)-\frac{\$ 5,000(1-.32)}{(1.0952)^{5}} \label{18.7}\]
We record the solution to this problem using Excel in Table 18.1 below.
| C10 | Function: | =NPV(C3,C4:C9) | ||
| A | B | C | D | |
| 1 | Finding the NPC of the Purchase | |||
| 2 | Purchase Price | $30,000.00 | ||
| 3 | rate | .095 | ||
| 4 | Depreciation tax savings period 1 | ($1,920) | ||
| 5 | Depreciation tax savings period 2 | ($1,920) | ||
| 6 | Depreciation tax savings period 3 | ($1,920) | ||
| 7 | Depreciation tax savings period 4 | ($1,920) | ||
| 8 | Depreciation tax savings period 5 | ($1,920) | ||
| 9 | After-tax salvage value period 6 | ($3,100) | ||
| 10 | NPV of depreciation tax savings + after-tax salvage | ($9,170.60) | “=NPV(rate, value1:value6) | |
| 11 | NPC: purchase price – (PV of tax-savings + salvage value) | $20.829.40 | “=NPV of depreciation tax savings + after-tax salvage plus the purchase price (C10+C2) | |
In cell C10 we enter the function: = NPV(rate,values) = NPV(C3,C4:C9) which returns the value ($9,170.60). In cell C11 we add the purchase price of $30,000 to the NPC of after-tax depreciation savings plus the liquidation value which returns the NPC of the purchase equal to $20,829.36.
Having found 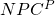 equal to $20,829.40, we can find C using Equation \ref{18.6}.
equal to $20,829.40, we can find C using Equation \ref{18.6}.
We solve this problem using Excel in Table 18.2 by finding the present value of Annuity Due with 5 payments of –1. We enter the arguments of the PV function and label the terms in adjacent cells. Excel’s PV function has the following arguments listed in column A: rate (rate), number of payments (nper), annuity (pmt), future value (FV), annuity type (type). For this problem, the discount rate is 9.5% = .095, the number of payments equals 5, the payments are –1, the future value FV is zero, and the type of annuity is an annuity due which requires we enter 1.
Table 18.2. Finding the PV
of the Annuity Due
Open Table 18.2 in Microsoft Excel
| B6 | Function: | =PV(B1,B2,B3,B4,B5) | |
| A | B | C | |
| 1 | rate | .095 | |
| 2 | nper | 5 | |
| 3 | pmt | -1 | |
| 4 | FV | 0 | |
| 5 | type | 1 | |
| 6 | PV | $4.20 | “=PV(rate,nper,pmt,FV,type) |
In cell B6 we type in the PV function: = PV(B1,B2,B3,B4,B5). The result returned is PV = $4.20. Then we multiply by (1 – T) as required in Equation \ref{18.6}. Finally we find C:
\[C=\frac{N P C^{P}}{(1-T)\left\{1+U S_{0}[r(1-\theta T), n-1]\right\}}=\frac{\$ 20,829.40}{.68(4.2)}=\$ 7,283.01 \label{18.8}\]
Now suppose that we wanted to know the number of periods required to reach a future value of $2,000. With the data already entered, we turn to the “goal seek” option in Excel. To access goal seek from the main menu, press the [Data] tab, then on the ribbon menu press the [What-if Analysis] button, and on the drop down menu press [Goal Seek…]. The goal seek menu allow us to identify a target value for a particular cell and a variable to change. In our case the target cell is B6 and the target amount is $2,000. The cell we allow to vary is the number of periods cell, B2. Then entering these into Excel’s solver, the solution returned is 18.57. Thus, by continuing to invest for 8.57 periods, we obtain a future value of $2,000 compared to the future value of $1,005.18 reached after 10 years of investing.
Alternatively, we could have asked what is the payment amount required to reach a future value of $2,000 during the original term. In this case we vary the annuity in cell is B3, and the solver returns the value of $182.65. Thus, by increasing our annuity due from $90 to $182.65, we reach a future value amount of $2,000 in the same term required to reach a future value of $1,005.18 with $90 annuity due payments.
What we have found in this example is that we would be indifferent between purchasing the truck for $30,000 and making five lease payments of $7,283.01. Obviously, the high discount rate of 14% and making the payment for the truck up front contributes to the high lease payment. In the questions at the end of this chapter, students will be asked to repeat the problem assuming the same values except that the opportunity cost of capital is 5%.
Comparative Advantages for Leasee and Leasor
So far, we have described the technical properties of leases and how a financial manager may decide between gaining control of a durable through a lease or purchase arrangement. In this section, we allow the lessee and the lessor to be two different persons whose comparative advantages lead them into an exchange arrangement in which one party purchases an asset and then leases it to another party. The solution in this case considers the NPC from the lessee’s (lessor’s) position, assuming that the lessor (lessee) pays their maximum bid purchase price (lease payment). What makes this an interesting problem is that differences in the lessee’s and lessor’s tax rates, as well as opportunity costs of capital, can create incentives to exchange.
Comparative advantage. A fundamental principle of economics is that firms should specialize in tasks for which nature, institutions, or luck has granted them an advantage. To illustrate, suppose two farmers, A and B, can both produce dry edible beans and carrots. Also assume A can grow dry edible beans and carrots more profitably than B, and B can grow carrots more profitably than it can grow dry beans. If both beans and carrots must be produced, then A should produce beans, and B should grow carrots. They could then trade to obtain what they did not produce, and both would be better off.
Even though A produced both beans and carrots more profitably than B, it would still be to A’s and B’s advantage to specialize. They should decide in which product A had the greatest advantage in production, or B had the least comparative disadvantage, and then specialize and trade as before.
An application of the law of comparative advantage explains why two firms may lease. Suppose firm A is able to purchase a durable at a lower price than firm B. But firm B, not firm A, has need of the services of the durable. In this case, firm A’s advantage is in purchasing while B’s advantage is in using the durable. Thus, A might purchase the durable and either sell or lease to B.
Another reason why A and B might both agree to lease has to do with relative tax rates. Suppose A, the purchaser of a durable, pays taxes at an average rate TP, which is higher than TL, the average rate at which B, the lessee, pays taxes. As the durable is depreciated, the depreciation creates a tax shield of greater value to the purchaser than to the lessee. Thus, we might say that A, the purchaser, has a comparative tax advantage over B, the lessee, in claiming tax depreciation. The lease allows the purchaser, A, and the lessee, B, to benefit from their comparative advantages associated with the tax shields created by depreciation.
Still further reasons why A and B might purchase and lease a durable are that they face different opportunity costs of capital, have different opportunities for using the durable’s services, or face different marginal costs of credit.
Comparative advantages for lessee and lessor
created by different tax rates and opportunity costs of capital. To
demonstrate the idea of comparative advantage with a lease
agreement, consider that person B, the lessee, will not lease for
more than it would cost to control the durable through a purchase
agreement. We want to find B’s NPC if the durable were purchased.
To simplify, assume the purchase price of the durable is
V0, the book value depreciation rate in year t
is 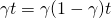 where t = 0, …, n – 1, rB is
B’s opportunity cost of capital, TB is B’s average tax
rate, and assume the lessee tax adjustment coefficient is 1. The
NPCP of the purchase for B is:
where t = 0, …, n – 1, rB is
B’s opportunity cost of capital, TB is B’s average tax
rate, and assume the lessee tax adjustment coefficient is 1. The
NPCP of the purchase for B is:
\[N P C^{L}(\text {purchase})=V_{0}-\frac{T^{B} \gamma V_{0}}{\left[1+r^{B}\left(1-T^{B}\right)\right]}-\frac{T^{B} \gamma V_{0}(1-\gamma)}{\left[1+r^{B}\left(1-T^{B}\right)\right]^{2}} -\frac{T^{B} \gamma V_{0}(1-\gamma)^{2}}{\left[1+r^{B}\left(1-T^{B}\right)\right]^{3}}-\cdots \label{18.9}\]
Equation \ref{18.9} is equivalent to Equation \ref{18.4} except that it is expressed in a form that makes it analytically tractable. Obviously, more detailed expressions with finite time horizons could easily be calculated. What makes Equation \ref{18.9} tractable is that it is expressed as an infinite series whose solution can be written as:
\[N P C^{L}(\text {purchase})=V_{0}-\frac{T^{B} \gamma V_{0}}{r^{B}\left(1-T^{B}\right)+\gamma} \label{18.10}\]
Now consider what happens to B’s NPC resulting from the purchase if B’s tax rate increases. We find the change in B’s NPC associated with the purchase of the durable by differentiating NPCP with respect to TB. (This operation in essence examines the change in NPCP with respect to a small change in TA. The results is that NPCP decreases with an increase in TB. Thus, a firm in a higher tax bracket can buy a durable at a lower after-tax cost than someone in a lower tax bracket.
Next, we find B’s NPCL associated with leasing the durable which, after summing geometrically, can be expressed as:
\[\begin{align} N P C^{L}(\text {lease}) &=\frac{C\left(1-T^{B}\right)}{\left[1+r^{L}\left(1-T^{B}\right)\right]}+\frac{C\left(1-T^{B}\right)}{\left[1+r^{L}\left(1-T^{B}\right)\right]^{2}} +\frac{C\left(1-T^{B}\right)}{\left[1+r^{L}\left(1-T^{B}\right)\right]^{3}}+\cdots \\[4pt] &=\frac{C\left[1+r^{L}\left(1-T^{B}\right)\right]}{r^{L}} \label{18.11} \end{align}\]
To illustrate Equation \ref{18.10} consider the
following example: Suppose Affordable Assets (AA) buys durables and
leases them to other firms. As a well-to-do established firm, AA’s
tax rate, TA is high—45 percent. On the other
hand, the Unendowed User (UU) lacks capital and
prefers to lease rather than own in order to protect its limited
credit. Because of its lower earnings, UU’s average tax rate
TU is 21 percent. In addition, assume
that the leased durable wears out at the rate of 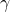 = 10 percent, and assume the market rate of return for both AA and
UU is 14 percent. Finally, assume that the purchase price of the
durable is $4,000.
= 10 percent, and assume the market rate of return for both AA and
UU is 14 percent. Finally, assume that the purchase price of the
durable is $4,000.
Making the appropriate substitutions into Equation \ref{18.10}, we find the NPC of purchasing the durable for UU is:
\[N P C^{U U}=\$ 4,000-\frac{[(.21)(.1)(\$ 4,000)]}{[(0.14)(1-0.21)+0.1]}=\$ 3,600 \label{18.12}\]
In other words, the after-tax purchase price of the durable for UU is $3,600.
Now consider the after-tax NPC of the purchase for firm AA. Making the appropriate substitutions into Equation \ref{18.10}, we find the NPC of purchasing the durable for AA is:
\[N P C^{A A}=\$ 4,000-\frac{[(0.45)(0.1)(\$ 4,000)]}{[(0.14)(1-0.45)+0.1]}=\$ 3,000 \label{18.13}\]
In other words, the after-tax cost of the durable purchase for AA was only $3,000 compared to $3,600 for UU.
Having calculated NPC for purchasing the durable for firms UU and AA, we can find their respective maximum bid lease prices. Making the appropriate substitutions into Equation \ref{18.11}, we find
\[NPC^{UU} (leasing) = \dfrac{C^{UU}[1 + (0.14)(1 – 0.21)]}{0.14} = \$3,600.\]
Solving for \(C^{UU}\) we find \(C^{UU} = \$453.81\).
Similarly we find
\[NP^{AA} (leasing) = \dfrac{C^{AA}[1 + (0.14)(1 – 0.45)]}{0.14} = \$3,000.\]
Solving for \(C^{AA}\) we find \(C^{AA} = \$389.97\).
Reflections on comparative advantages for firms UU and AA. Because of their differences in tax rates, firms UU and AA have different effective after-tax cost of the durable even though the market price of the durable is the same for each firm. In this case, the effective cost for AA is less than for firm UU—$3,000 versus $3,600. On the other hand and as a result of the differences in the effective after tax cost of the durable, the maximum bid lease price for firm UU is greater than for firm AA: $453.81 versus $389.97.
These results provide opportunities for firms AA and UU to take advantage of their comparative advantages: firm AA purchases the durable at a lower effective cost than is available to UU. UU, on the other hand, is quite willing to pay a higher lease price than AA’s maximum bid lease price. Under these arrangements, both firms AA and UU are made better off.
Leases and NPV. Assume that firm AA buys the durable and UU leases the durable from AA. Now the lease price in an expense for firm UU but an income for AA. We may want to ask: what is the minimum lease payment AA could accept from UU and still break even? To find this amount we set AA’s NPV as:
\[N P V^{A A}=\frac{C\left[1+r\left(1-T^{A A}\right)\right]}{r-N P C^{A A}(\text {purchase})} \label{18.14}\]
After making the appropriate substitutions we find
\[C=\frac{N P C^{A A}(\text {purchase})\left(r^{A A}\right)}{\left[1+r^{A A}\left(1-T^{A A}\right)\right]}=\frac{\$ 3,000(.14)}{[1+(.14)(1-.45)]}=\$ 389.97 \label{18.15}\]
Thus, any arrangement with UU which generates a lease payment more than $389.97 will result in a positive NPV for AA.
Summary and Conclusions
Trades occur when each party to the exchange gives up something of value in return for something of greater value. In most trades, a physical object or service is exchanged for an agreed-on amount of cash. Moreover, in most cases, ownership is transferred along with the good or service.
This chapter has considered leasing, a different kind of trade, in which the control over the use of a durable is transferred, but ownership of the durable is not. Leasing exists because it provides benefits to the lessee and lessor that might not be realized if control of a durable also required ownership.
Different types of leases described in this chapter include sale-and-leaseback agreements, operating leases, and financial or capital leases. Leases offer particular advantages for lessees including the avoidance of capital requirements associated with a purchase. As a result, lessees may use their limited credit for other purchases or as a credit reserve. Obsolescence risk of ownership is also reduced for lessees. Additionally, leasing offers the chance to better match service requirements to the delivery of services. Ownership of durables may require holding idle capacity—less likely when services of a durable are leased.
Tax considerations are critical in the decision to lease or to purchase. Ownership allows for tax depreciation shields; leasing allows the entire lease payment to be claimed as an expense.
An important principle of comparative advantage is involved in the lease decision. If the tax depreciation from ownership is greater for one firm than for another, leasing permits the firm which can benefit the most from the depreciation shield to claim it by purchasing the asset and leasing it to another firm. Not only can comparative tax advantages be optimally used through leasing, there can also be comparative advantages in acquiring financing. Comparative advantage and the incentive to lease may also result from differences in opportunity costs, access to credit, and use for the durables’ services. In essence, leasing is a critical tool that allows firms to benefit from their comparative advantages.
Questions
- Describe three different lease types and their essential differences.
- For every lease agreement, there is a lessor and a lessee who both believe they will be better off by executing the lease. Describe how a sale and leaseback agreement might make both the lessor and lessee better off.
- Assume a lease agreement that requires $100 payments at the beginning of each period for 15 years. The lessee’s marginal tax bracket is 25% and opportunity cost of capital is 8%. The tax adjustment coefficient is assumed to equal 80%. Find the NPC of this lease. Now assume that the lessor agreed to accept payments at the end of each period instead of the beginning. What would be the NPC of the lease agreement under the new arrangement?
- Resolve the Go Green lease problem assuming that the firm’s opportunity cost of capital is 5% rather than 14%. Compare your solution with the previous one. Did the lease payment go up or down? Can you explain why?
- Resolve the Go Green lease problem by assuming that the lessee will lease the durable for an extra period. The lessee will make 6 lease payments instead of 5, but the depreciation schedule will not change. In other words, find the maximum lease payment and explain your results.
- Explain in your own words the concept of comparative advantage. Provide one example of how the concept of comparative advantage has influenced your choice or the choice of others.
- Explain how the principle of comparative advantage might explain why two firms may agree to a lease arrangement.
- In the example of a lessee UU and a lessor AA, the lessee and lessor are in different average tax brackets (45 versus 21 percent) but were assumed to face the same opportunity cost of capital. Resolve the example by assuming UU’s opportunity cost of capital is 7% instead of 14%. Find the effective after-tax purchase price of the durable for the two firms. Then find the maximum bid lease price for the two firms. Do the results allow for the two firms to take advantage of the principle of comparative advantage? Please explain.
- Consider the case of firms UU and AA described in the text. Since AA has the lowest NPC for purchasing the durable, it should do so. Meanwhile the maximum bid lease price for UU is higher than for AA, so UU should lease rather than purchase the durable. Suppose that UU agrees to pay AA a lease price of $410.00. What is AA’s NPV from buying the durable and leasing it back to UU? (Hint: In this arrangement, the lease cost for UU is an income for AA.)


