16: Loan Analysis
- Page ID
- 12761
After completing this chapter, you should be able to: (1) understand the different ways interest can be calculated on a loan; (2) recognize the different kinds of interest rates that are used to calculate interest costs on loans; (3) computer comparable interest rates by finding a loan’s effective interest rate; (4) use Excel worksheets to calculate the loan payment, interest rate, term, elasticity of term, and amortization schedule for a particular loan; and (5) evaluate alternative loans using present value (PV) models developed earlier.
To achieve your learning goals, you should complete the following objectives:
- Learn the differences between the following interest rates: the annual percentage rate (APR), the actuarial rate, and the effective rate.
- Learn how to compute the APR, the actuarial rate, and the effective rate on alternative loans.
- Learn how to use the loan equality equation to find a loan’s effective interest rate, its constant payment, its term, and its original loan amount.
- Learn how to find the elasticity relationship between interest rates, loan payments, and the term of the constant payment loan.
- Learn how to create an amortization table for constant payment loans.
- Learn how to find break-even points for refinancing loans.
- Learn how to find the effective rate for several disguised interest rate loans including discount loans and points added loans.
Introduction
Loan formulas and PV models have many similarities. Interest rates on loans are like opportunity costs, the loan amount is like an investment, and loan payments are like an investment’s cash flow. These and other similarities between PV models and loan formulas allow us to use PV tools to analyze different types of loans. The next section focuses on alternative interest rate definitions. This chapter will also identify the relationship between the term of a loan and the size of the loan payment. Finally, this chapter finds break-even points when refinancing loans and effective interest rates for a variety of disguised interest rate loans.
Comparing the Actuarial Rate, Annual Percentage Rate (APR), and Effective Interest Rate
Loans charge interest rates of which there are at least three kinds that are closely related to each other. These rates and their commonly used synonyms are listed below. The interest rate name used in this chapter is italicized. They are: (1) actuarial rate, compound rate, true rate, or periodic rate; (2) Annual Percentage Rate (APR), annual rate, or nominal rate; and (3) effective interest rate or effective annual rate.
Actuarial Rate. In financial transactions, interest may be computed and charged more than once a year. For example, interest on savings deposits is usually calculated on a daily basis while many corporate bonds pay interest on a semiannual basis. The interest rate used in computations for periods of less than one year is called an actuarial interest rate. The actuarial rate is defined as the interest rate per compounding period or the interest rate per period of conversions. It is the actuarial rate used to charge interest on the principal sum during each successive conversion period. For example, consider a 1% actuarial rate charged monthly on $1,000. In this case, in the first month of the loan, 1% of $1,000 or $10 of interest is charged. In the second month, interest is charged on $1,010 equal to $10.10, etc.
Annual Percentage Rate (APR). Let rf represent the APR. Let m stand for the number of times during the year the interest is calculated or charged. Thus, m equals the number of compounding periods per year. The ratio of rf / m is the actuarial rate, the compound rate, the true rate, or the periodic rate.
We find the APR from actuarial rates by expressing the actuarial rate on an annual basis. To convert the actuarial rate to an APR, we multiply the actuarial rate by m. In the previous example, we multiply the actuarial rate of 1% per month by 12 to yield an APR of 12%. When the compound period or conversion period is one year in length, then the actuarial rate and the APR are equal.
Consider two savings institutions, both offering the same APR. The only difference is that institution A offers monthly compounding of interest, while institution B offers annual compounding. Which one should the saver prefer? Obviously, monthly compounding is preferred because the saver earns interest on the interest earned during the same year. With institution B, interest is earned during the year only on the principal saved and on interest earned in previous years.
Effective interest rates. Effective interest rates are the actual interest charged measured on an annual basis. When APRs have different numbers of compound periods per year, the different actuarial rates should be converted to their effective interest rates for comparison. The effective rate is obtained by compounding the actuarial rate for a period of one year. As the number of compounding periods per year increases, the difference between the APR and the effective rate increases.
Relationship between interest rates. The relationships between an actuarial rate, an APR, and an effective rate can be easily summarized. Let m be the number of compounding periods per year, let rf be the APR, let rf/m be the actuarial rate, and let re be the effective rate. The relationship between the effective rate re, the APR rate rf, and the actuarial rate rf/m can be expressed as:
\[r^{e}=\left[\left(1+\frac{r^{f}}{m}\right)^{m}-1\right] \label{16.1}\]
Note that when m = 1, the effective interest rate, the APR rate, and the actuarial rate are equal. However, when m is not 1, the rates are no longer equal. For example, suppose we wish to find the re assuming rf were compounded quarterly. To solve this problem let m = 4, and rf = 12. Substituting .12 for rf and 4 for m in Equation \ref{16.1}, we obtain the results described in Table 16.1 using Microsoft Excel. In cell B3 we enter the function fx = ((1 + (B1 / B2))^B2) – 1 which returns 12.55%.
| B4 | Function: | =(1+B2/B3)^B3 -1 | |
|---|---|---|---|
| A | B | C | |
| 1 | Finding an effective interest rate | ||
| 2 | APR | 0.12 | |
| 3 | m | 4 | |
| 4 | effective rate | 12.55% | “=(1 + APR/m)^m – 1 |
If m is increased to 12, or monthly compounding periods, the effective rate is found as before. Let m = 12, and rf = 12 in Equation \ref{16.1}. Then
\[\left[\left(1+\frac{.12}{12}\right)^{12}-1\right] \label{16.2}\]
To solve this equation in Excel, we change cell B3 to 12 and find the effective interest rate to equal 12.68% as shown in Table 16.2.
| B4 | Function: | =(1+B2/B3)^B3 -1 | |
|---|---|---|---|
| A | B | C | |
| 1 | Finding an effective interest rate | ||
| 2 | APR | 0.12 | |
| 3 | m | 12 | |
| 4 | effective rate | 12.68% | “=(1 + APR/m)^m – 1 |
A special compounding formula is obtained by allowing the number of periods compounded to be very large. This idea is expressed as:
(16.3)
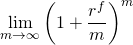
which means that as m approaches infinity the effective rate re equals:
(16.4)
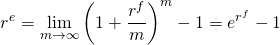
To solve this problem using Excel, we use the EXP function. In Excel, Euler’s number “e” is found as the function EXP(1) and 12% compounded continuously can be calculated as fx = EXP(.12) – 1 = 12.75. Using the previous cell designation, to find the value of continuously compounding of 12% we would enter the formula in B4 as: fx = EXP(B2) – 1 = 12.75.
| B4 | Function: | =EXP(B2) – 1 | |
| A | B | C | |
| 1 | Finding an effective interest rate | ||
| 2 | APR | 0.12 | |
| 3 | m | Infinite | |
| 4 | effective rate | 12.75% | “=EXP(APR) – 1 |
Constant Payment Loans
Having defined interest rates in financial models, we now use PV models to analyze the most common type of loan, the constant payment loan. Constant payment loans are repaid with a series of equal payments A at equal time intervals. These payments may occur m times during a year over n years, yielding a total of mn payments.
The fundamental equality is that the sum of the
loan payments discounted at the actuarial interest rate must equal
the amount loaned. The relationship between loan amount, 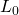 ,
received in time-period zero, with payment A, made for
mn periods, at actuarial interest rate
(rf/m) beginning in period one, is:
,
received in time-period zero, with payment A, made for
mn periods, at actuarial interest rate
(rf/m) beginning in period one, is:
\[L_{0}=\frac{A}{1+\frac{r^{f}}{m}}+\frac{A}{\left(1+\frac{r^{f}}{m}\right)^{2}}+\dots+\frac{A}{\left(1+\frac{r^{f}}{m}\right)^{m n}} \label{16.5}\]
In this formula, the actuarial rate (rf/m) is the IRR for the PV model, and since loan payments are constant, it is unique.
A sum that will prove useful in several calculations is the following:
(16.6)
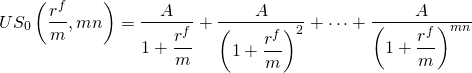
The notation US0(rf/m, mn) stands for the present value of a uniform series of $1 payments discounted at the actuarial rate (rf/m) for (mn) periods. This shorthand notation allows us to rewrite Equation \ref{16.2} as:
(16.7)
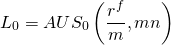
Recall that with one equation we can solve for at most one unknown variable. From Equation \ref{16.7} if we know A and US0(rf/m, mn) we can find loan amount L0 that mn payments of amount A discounted at actuarial rate (rf/m) will repay.
Suppose we solve for A in Equation \ref{16.7}. The result is:
(16.8)
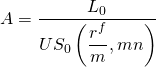
From Equation \ref{16.8} if we know L0 and US0(rf/m, mn), we can find constant loan payment A, that, if discounted at actuarial rate (rf/m) for mn periods, will repay loan amount L0.
Suppose we solve for US0(rf/m, mn) in Equation \ref{16.7}. The result is:
(16.9)
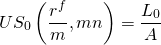
If we know A and loan amount L0 in Equation \ref{16.9} we can find rf, m, or n, that constant loan payment A discounted at actuarial rate (rf/m) for mn periods will repay.
Fortunately, the calculations described in equations (16.7), (16.8), and (16.9) can be easily performed using Excel.
Example \(\PageIndex{1}\): Loan amount supported by a constant payment loan
Suppose a borrower can make constant payments of $150 per month for 48 months (four years). The borrower wants to know what size loan can be repaid if the APR interest rate is 5% and the actuarial rate is .05/12 = 0.42%. Using Equation \ref{16.8} we can solve for the loan amount supported by the constant loan payment of $150 using the formula below:
(16.10)
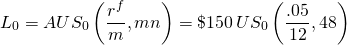
We solve the equation above using Excel’s PV function in Table 16.4.
| B7 | Function: | =PV(B3/B4,B4*B5,B6,,0) | |
| A | B | C | |
| 1 | Finding the loan amount in a constant payment loan | ||
| 2 | |||
| 3 | rate | .05 | |
| 4 | m | 12 | |
| 5 | n | 4 | |
| 6 | pmt | -150 | |
| 7 | PV | $6,513.44 | “=PV(rate/m,mn,pmt,,0) |
The answer displayed is: $6,513.44. In other words, 48 monthly payments of $150 on a loan charging a 5% APR interest rate and a monthly actuarial interest rate of .42% will repay a loan in the amount of $6,513.44.
Example \(\PageIndex{2}\): Constant Payment Loan Annuities
Suppose $5,000 is borrowed from a lending institution for five years at an APR of 12% or a monthly actuarial rate of 1%. The loan is to be repaid with 60 equal monthly installments. What is the payment or annuity necessary to retire the loan?
Using Equation \ref{16.4} we can solve for the payment that repays the $5,000 loan:
(16.11)
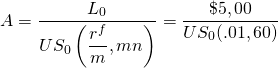
We solve for the loan payment using Excel’s PMT function in Table 16.5. The answer displayed is: –$111.22 which means that 60 payments of $111.22 on a loan charging 12% APR interest and a monthly actuarial interest rate of 1% will repay a loan in the amount of $5,000.
| B6 | Function: | =PV(B3/B4,B4*B5,B7,,0) | |
| A | B | C | |
| 1 | Finding the loan amount in a constant payment loan | ||
| 2 | |||
| 3 | rate | 0.12 | |
| 4 | m | 12 | |
| 5 | n | 5 | |
| 6 | pmt | ($111.22) | “=pmt(rate/m,mn,PV,,0) |
| 7 | PV | $5,000.00 | |
Example 16.3. Loan term required to retire a constant payment loan. Suppose a borrower can make constant payments of $150 per month. The borrower wants to know how many monthly payments will be required to retire a loan of $8,000 if the APR interest rate is 6% and the monthly actuarial rate is .5%. Using Equation \ref{16.9} we can solve for the term of the loan required to retire the loan.
(16.12)
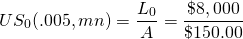
We solve the equation using Excel’s NPER function shown in Table 16.6. The answer displayed is 62.19 which means that 62 regular payments and one partial payment will be required to retire a loan of $8,000 if the APR interest rate charged on the loan is 6%.
Table 16.6. Finding the
Number of Payments required to Retire a Loan
Open Table 16.6 in Microsoft Excel
| B8 | Function: | =NPER(B3/B4,B6,B7,,0) | |
| A | B | C | |
| 1 | Finding the number of payments required to retire a loan | ||
| 2 | |||
| 3 | rate | 0.06 | |
| 4 | m | 12 | |
| 5 | n | ||
| 6 | pmt | -150 | |
| 7 | PV | $8,000.00 | |
| 8 | nper | 62.18593 | “=NPER(rate/m,pmt,PV,,0) |
Comparing Interest Paid, Loan Term, and Payment Amounts for Constant Payment Loans
An important relationship exists between the loan’s term and total interest paid. To illustrate, consider a $30,000 loan at 15% APR to be repaid in monthly payments over 30 years. The monthly payment for this loan is $379.33. Total interest TI paid on a constant payment loan is found by multiplying the constant loan payment A times the term of the loan mn, minus the amount of the loan L0:
(16.13)
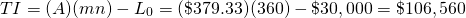
In this case, the total interest paid is $106,560.
Increasing the payment amount by 10% to $417.27 reduces the term of the loan by 48% to just over 15.36 years (verify the results above using Excel). Meanwhile, total interest paid is reduced by 56% to $46,961.
The term reduction in response to an increased loan payment is not always so significant. For example, if the above loan had an 8% APR, the monthly payment would equal $220.13 instead of $379.22. Increasing the payment by 10% would decrease the term of the loan by only 27% from 30 years to 21.93 years, and the total interest paid would be decreased by 32% from $49,247 to $33,722.
It would be useful to know how changing the term of the loan affects payment size and total interest paid. It can be shown that as mn becomes large, the payment A approaches the interest cost per period, i.e., the smallest payment possible equals the interest charged on the outstanding loan balance. If the borrower wished to minimize his or her payment, the appropriate term is the one that permits the borrower to repay only interest. The shortest repayment period, on the other hand, is one. Obviously, there is a trade-off between the size of the loan payment and the length of the loan.
The point elasticity of term, measured in years n with respect to the payment A, measures the percentage change in the term n in response to a 1% change in the loan payment. The term elasticity, E(n,A), has been calculated as:
(16.14)
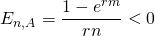
For example, a 30-year loan and an APR of 15% would have an elasticity of term equal to:
(16.15)
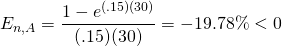
In other words, increasing the payment by 1% would decrease the term by approximately 19.78%. In contrast, the arc elasticity, rather than the point elasticity, compares the percentage change in the loan term to a 10% increase in the loan payment and finds the percentage change in the term to equal 48%, or an arc elasticity of term equal to 4.8%. Note that a point elasticity of 19.78% versus an arc elasticity of 48% is the result of comparing large changes in loan payments of 10% versus comparing tiny changes in loan payments (e.g. .00001%). See Table 16.7 of point elasticities below.
Table 16.7. Point elasticity measures for loans of alternative terms and interest rates.
| n / r % | 1% | 5% | 7.5% | 10% | 15% | 20% |
| 1 | 1.01 | 1.03 | 1.04 | 1.05 | 1.08 | 1.11 |
| 5 | 1.08 | 1.14 | 1.21 | 1.30 | 1.49 | 1.72 |
| 10 | 1.17 | 1.30 | 1.49 | 1.72 | 2.32 | 3.19 |
| 15 | 1.26 | 1.49 | 1.85 | 2.32 | 3.77 | 6.36 |
| 20 | 1.37 | 1.72 | 2.32 | 3.19 | 6.36 | 13.40 |
| 25 | 1.49 | 1.99 | 2.94 | 4.47 | 11.07 | 29.48 |
| 30 | 1.49 | 2.32 | 3.77 | 6.36 | 19.78 | 67.07 |
| 60 | 2.99 | 6.36 | 19.78 | 67.07 | 900.23 | 13,563.00 |
Example 16.4.Term and Loan Payment Trade-Offs. Lucy Landlord is financing the renovation of a property. She needs a loan for $28,000. Her lender offers her a loan for 20 years at the current interest rate of 15%. She calculates her annual payment to be $4,473.32. If she increases her payment by 1% to $4,518.05, her term is reduced to 19 years, or a reduction of 5%. This percentage reduction is nearly equal to the tabled value of 6.36 in the Table 16.1, found at the intersection of the row labeled 20 and the column labeled 0.15. Large percentage increases in A, such as 10%, may not be accurately reflected in the table of point elasticities. This is because the percentage changes in n with respect to A are large compared to the very small changes in n with respect to A used to calculate the table.
Creating an Amortization Table for Constant Payment Loans
The word “amortize” originally meant “to kill.” Thus when we amortize a loan, we kill or extinguish it by making regular payments—killing the loan if you will. One feature of the constant payment loan is that, while the loan payment is constant, the amount of the payment devoted to paying off the loan—the principal portion of the payment—and the amount of the payment devoted to paying the interest on the loan are constantly changing. As the loan principal is reduced or killed off, the amount of the payment devoted to interest charges is reduced and the amount of the payment devoted to reducing the loan is increased. Lending institutions, when asked, will provide amortization tables that detail the amount of interest and principal paid on each payment during the life of the loan. Fortunately, Excel provides us the tools needed to create our own amortization tables.
Finding principal portion of the tth loan payment using Excel. The Excel PPMT function can be used to find the principal portion of the tth loan payment. The function is expressed as:
(16.16)
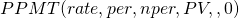
To illustrate the PPMT function, consider at $25,000 loan to be repaid in monthly installments for four years. The APR for the loan is 5%. We want to know what portion of the 5th payment (period) will be applied to the loan’s principal. The Excel solution is represented in Table 16.8.
Table 16.8. Finding the Loan
Principal Paid on the tth Payment
Open Table 16.8 in Microsoft Excel
| B8 | Function: | =PPMT(B3/B4,B6,B4*B5,B7,,0) | |
| A | B | C | |
| 1 | Finding the loan principal paid on the tth payment | ||
| 2 | |||
| 3 | rate | 0.05 | |
| 4 | m | 12 | |
| 5 | n | 4 | |
| 6 | period | 5 | |
| 7 | PV | $25,000 | |
| 8 | Principal paid | ($479.47) | “=PPMT(rate/m,period,m*n,PV,,0) |
It turns out that $479.47 of the 5th payment is applied to the outstanding loan principal. In addition, students may verify that the principal portion of the 25th payment is $521.05. This is because the outstanding principal on which interest is charged decreases over the life of the loan. As interest decreases, more of the loan payment can be applied to the outstanding loan principal.
Finding interest payment IP(t) on the tth loan payment using Excel. The Excel IPMT function can be used to find the interest portion of a loan payment in the tth period and is expressed as:
(16.17)
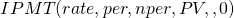
To illustrate the IPMT function, we return to the earlier example: a loan amount of $25,000, a term of 48 monthly payments, at 5% APR, and a desire to find the interest paid on the 5th loan payment. We illustrate the Excel solution for finding interest paid on the tth period. The solution is entered in cell B8 as $54.68. Table 16.9 describes the solution in more detail.
Table 16.9. Finding the Loan
Interest Paid on the tth Payment
Open Table 16.9 in Microsoft Excel.
| B8 | Function: | =IPMT(B3/B4,B6,B4*B5,B7,,0) | |
| A | B | C | |
| 1 | Finding the loan interest paid on the tth payment | ||
| 2 | |||
| 3 | rate | 0.05 | |
| 4 | m | 12 | |
| 5 | n | 4 | |
| 6 | period | 5 | |
| 7 | PV | $25,000 | |
| 8 | Interest paid | ($96.26) | “=IPMT(rate/m,period,m*n,PV,,0) |
Together, the interest payment of $96.26 and the principal payment of $479.47 equals the constant loan payment of $575.73.
PVs of Special Loans
Loans and credit (one’s borrowing capacity) make possible a modern economy and successful firms. Sometimes sellers offer special loan arrangements to encourage the potential buyers to purchase their products. These may include concessionary interest rate loans, skip payment loans, skip principal payment loans, variable interest rate loans, and balloon payment loans. Other times firms may want to expand their investment base and need to refinance their loans, or decreases in interest rates may provide them an incentive to refinance. Fortunately, all of these special loans can be analyzed using PV models developed earlier. We consider the benefits and costs of several special loans in what follows.
Concessionary interest rate loans. Assume that Jane Doe’s IRR = r is 10%. Recall that an IRR is the opportunity cost of the defender and is the appropriate rate to use when discounting investment cash flow. Jane is considering an investment loan for $50,000 to be repaid in monthly installments over 15 years (mn = 180). The APR for the loan is 7%, while the actuarial rate is 7% / 12 = .58%.
To find Jane’s NPV for this loan, we first determine her loan payment A. This we can do using the Excel function PMT(rate,nper,PV,,0) = PMT(.58,180,$50,000,,0). The payment A for this loan is: $449.41.
The next step is to treat the loan payment as a cash flow in an investment problem and discount the payments using the borrower’s IRR = r of 10%, or the borrower’s actuarial opportunity cost rate of 10%/12=.83%. Using Equation \ref{16.3}, we find:
(16.18)
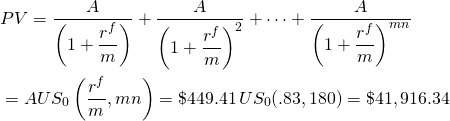
Some interpretation of the above results may be helpful. The first important fact is that the borrower’s IRR(r = 10%) was more than the interest rate on the loan (rf = 7%). Therefore the borrower can borrow at a rate less than what she will earn by investing the loan. The borrower’s actual cost of the loan, what is paid back after adjusting for what the loan earns as an investment, is $41,916.34, not $50,000. Another way to express this result is that present value of the loan was $41,916.34. The Net Present Value (NPV) of the $50,000 loan is:
(16.19)
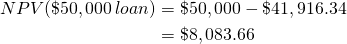
In other words, the borrower received in the form of a loan $50,000 in present value dollars. What the borrower paid back in present value dollars was $41,916.34. The difference—the NPV—was $8,083.66.
Refinancing a Constant Payment Loan. A common financial transaction is the refinancing of a constant payment loan. What complicates this transaction is loan closing costs or points charged as a percentage of the loan required to close. If the current interest rate is less than one’s interest rate on the existing loan, a reasonable borrower would prefer to refinance. What if refinancing requires a fee, percentage points charged as a percentage of the new loan, to be paid at the loan closing? We want to know what the borrower can afford to pay as a refinancing cost, or points of the loan to break even. Finding break-even points is what we do next. We will use as our starting point the numbers introduced into the previous example.
The refinance problem is clearly an NPV problem. Its solution requires that we identify which is the defending and which is the challenging investment. The defender in this case is the loan the borrower now holds. The challenger is the new loan with its reduced interest rate and points charged to close the loan. What the borrower will earn on the loan is not relevant here because we assume that those earnings will be the same regardless of whether they are financed with the new loan or continue to be financed with the old loan.
To solve this problem, we recognize that if the PV of loan payments on the new loan plus points charged to close the loan is the same as the PV of loan payments on the old loan (and ignoring taxes), points charged are break-even. So using Equation \ref{16.8}, we find break-even points charged to refinance as:
(16.20a)
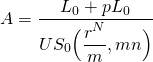
where pL0 is the cost the borrower pays to refinance the loan, p percent of the new loan must be paid as a refinance cost, and rN is the interest rate on the new loan. The loan payment on the old loan is:
(16.20b)
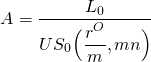
where rO is the interest rate on the old or original loan. Finally, equating equation (16.20a) to (16.20b) and solving for p, we find the break-even points to refinance the loan; that is, we find the percentage of the loan p that could be paid as a refinancing charge by the borrower to obtain a loan with a lower interest rate and still break-even. The formula for p is:
(16.21)
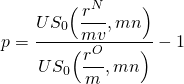
To illustrate, let rO = 8%, rN = 6%, and let mn = 180. We first solve for p using Excel:
(16.22)
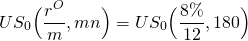
by keying in PV(rate,nper,PMT,,0) = PV(.66,180,1,,0) and find:
(16.23)
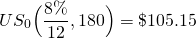
We follow the same procedures to find:
(16.24)
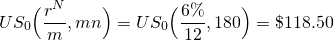
Finally, we find p by making the appropriate substitutions into Equation \ref{16.21}:
(16.25)
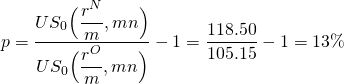
A variation of the problem would be the following: Suppose that we knew what points would be charged to refinance the loan, and we wanted to know what APR would be required to be indifferent between the new and old loan. In other words, we want to find the break-even rN given that we know p, the points charged to refinance the loan. The solution is found by rearranging Equation \ref{16.9} so that:
(16.26)
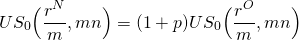
To illustrate, suppose that p is known to be 10%, and the conditions attached to the old loan are as before, so that:
(16.27)
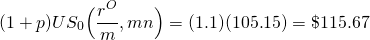
To find the break-even APR on the new loan we equate:
(16.28)
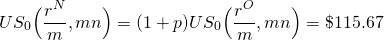
We now solve this problem using Excel RATE function:
(16.29)
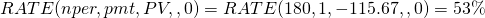
Displayed is the break-even actuarial rate, .53, which when multiplied by 12 equals the break-even loan rate of 6.38%. Compared with our earlier results, if points paid to refinance the loan were reduced from 13% to 10%, the borrower could afford to pay 6.38% on the new loan and still break even.
Consider another example with p = 15% in the previous example. First equate:
(16.30)
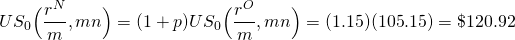
To find the corresponding interest rate for US0(rN/12, 180) = $120.92, we key into Excel’s RATE function:
(16.31)
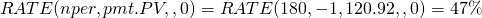
The answer displayed is: .47 which, when multiplied by 12, equals the break-even loan rate of 5.69%. Before, a new interest rate of rN = 6% corresponded to break-even points of 13%. If points charged were 15% instead of 13%, the new interest rate would need to equal 5.69% to be indifferent between continuing with the old loan versus paying closing costs and taking out a new loan.
Practical refinance problems facing agricultural firms. Agricultural firms in particular face cash receipts variability. This means that firm’s liquidity measures such as the current ratio (CT) or the times-interest-earned (TIE) ratio may also face significant variability over time making mortgage payments problematic. And sometimes, the original mortgage for an investment was written for a much shorter period than the investment’s productive life. Whatever the case, liquidity concerns may require the firm to renegotiate the terms of their loans with their lenders. To illustrate, consider the payment calculated in Example 16.2. In this case the required payment was found to equal $111.22. Suppose the lender were willing to increase the term of the loan by 12 monthly payments. What would be the new loan payment? Resolving the Excel PMT function returns:
(16.32)
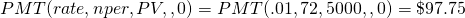
The solution is the loan payment that will retire a loan of $5,000 with 72 payments rather than 60 payments at an actuarial rate of 1%. The loan payment is reduced from $111.22 to $97.75.
Disguised Interest Rates and Effective Interest Rates
One of the challenges financial managers face when considering borrowing decisions is knowing the actual cost of borrowing—or, stated another way, knowing the effective APR interest rate. Sometimes lenders offer loans designed to disguise the real cost of their loans. We call their loans disguised interest rate loans. Disguised interest rate loans have effective interest rates increased by methods other than increasing the interest rate on the loan. For example, interest costs can be subtracted in the initial period, reducing the actual loan amount received by the borrower (a discount loan). Interest can be charged as though the original loan balance was outstanding throughout the life of the loan (an add-on loan). Alternatively, the lender can charge a loan closing fee, reducing the actual loan balance received by the borrower. Additionally, the interest can compound more frequently than loan payments occur. Each of these methods will increase the effective interest rate above the stated interest rate. Consider several types of disguised interest rate loans.
The Discount Loan: A borrower approaches his lender for a loan of L0 for mn periods. The borrower learns that the stated interest rate or disguised interest rate is rd. When the borrower picks up the check for his loan, the amount he receives equals only:
(16.33)
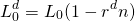
the amount of the loan requested less the stated interest rate times the term of the loan. Meanwhile, the constant loan payment is calculated as:
(16.34)
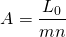
To calculate the APR associated with this loan, treat payments of amount A as if they were associated with a constant payment loan that retires a principal amount of Ld. The relationship is expressed as:
(16.35)
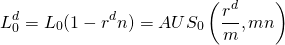
Next, substituting for A, L0/mn, we find:
(16.36)
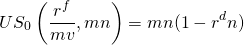
To illustrate the discount loan, assume a consumer obtains an installment loan for $10,000, from which $2,500 is deducted for interest costs. The loan is to be repaid over 2 years, with monthly payments equal to $416.67 = ($10,000/24). To solve this example, we first must find the stated rate rd:
(16.37)
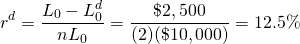
Normally, the stated rate is given, but it is advisable to confirm the rate as we have done above. Now we enter our numbers into Equation \ref{16.36} and obtain:
(16.38)
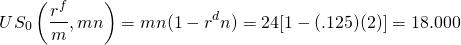
To find the actuarial rate, we key into our Excel RATE function:
(16.39)
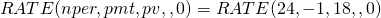
Displayed is the actuarial monthly rate of 2.44% or, after multiplying by 12, we find the corresponding APR rate of 29.3%. The effective rate re is: re = (1.0244)12 – 1 = 33.55%.
This is quite a difference compared to the stated interest rate of 12.5%. Hence, the discount loan effectively disguises its true APR.
Points-added loans. Sometimes lenders charge points p to close a loan. The fee has the effect of increasing the interest rate on the loan since the lender earns more than the stated rate suggests. The APR rate for such a loan can be calculated by first computing the payment which retires the loan, plus the points added. The payment equals:
(16.40)
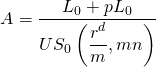
Next, express the relationship between the payment A in Equation \ref{16.40}, APR rate rf, and the actual amount of the loan received as:
(16.41)
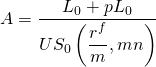
Equating equations (16.40) and (16.41), we find rf from the equality:
(16.42)
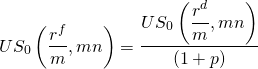
To illustrate how to find the effective interest rate for a points-added loan, consider the following problem. A bank offers a loan rate of 12% with monthly payments for three years, with a 3% loan-closing fee. What is the APR interest rate rf? Using Equation \ref{16.42} we first find:
(16.43)
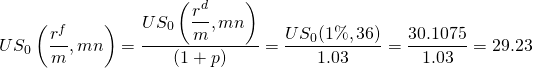
To find the true actuarial rate, we key into our Excel RATE function:
(16.44)
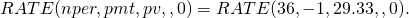
Displayed is the actuarial monthly rate of 1.15%, or after multiplying by 12, we find the corresponding APR rate of 13.83%. The effective rate re is: re = (1.0115)12 – 1 = 14.71%. This is quite different compared to the stated interest rate of 12%.
Summary and Conclusions
In this chapter we demonstrated the versatility of PV models by using them to analyze loans. For constant payment loans, we used PV models to solve for constant loan payments, terms, loan amounts, and interest rates—remembering that one PV equation can solve for at most one unknown.
Using PV models to analyze loans required that we identify the various kinds of interest rates. This was an important exercise because we discovered the difference between stated interest rates and effective interest rates—the interest rate actually paid on the loan funds made available.
Another important exercise was discovering the sensitivity of the relationship between the size of the loan payment and the term of the loan. In most cases, the relationship is not one-to-one. In other words, a 1% increase in the size of the loan payment rarely leads to a 1% drop in the term. The corresponding percent decline in the term of the loan is usually much, much more. Hence, we discovered that, when applying for loans, it pays to explore various terms and sizes of loan payments and find the best match—the one with the optimal trade-off between term and liquidity.
A common problem is that existing loans often need to be refinanced. Such may be the case when interest rates drop or a project currently financed is expanded and additional funds are required. In the text we considered refinancing existing loans and found break-even loan closing points. In the supplemental materials at the end of this chapter, we will find the more general formula for refinancing when the term, interest rate, and size of the new loan may be different than on the existing loan.
Lastly, we demonstrated how some loans may disguise the true interest rate. While we only illustrated the solution for the discount loan and the points-added loan, there are several other kinds of loans that disguise the true interest rate.
Questions
- Which would you prefer to earn on your savings? An APR rate of 12.5% or a 1% actuarial rate compounded monthly? Given an APR of r percent, what is the most that the effective rate can earn above the APR rate if it is compounded continuously?
- Consider a loan of $80,000 at an APR of 13%. What is the loan payment that would retire the loan if repaid in monthly payments for 10 years? If repaid in monthly installments for 9 years? Compare the percentage change in the term versus the percentage change in the loan payment (the arc elasticity). Finally, find the point elasticity E(n,A) on the original loan.
- Assume a loan of $54,000 with a remaining term of 21 years. The existing loan requires monthly payments at an APR of 11.25%. For a 3% closing fee, the borrowers could refinance their loan at an APR rate of 10% for the same term. What is the effective interest rate on the new loan? What are the break-even points for refinancing the loan? What is the total interest paid on the two loans?
- A consumer obtains an installment loan of $12,000 from which $2,700 is deducted for interest costs. The loan is to be repaid over two years with monthly payments equal to $500 ($12,000/24). Please determine the effective interest rate re on this loan.
- A farm supply store offers its customers 30 days same-as-cash arrangements. That is, for bills paid within 30 days after purchases are made, no interest is charged. On the other hand, to encourage early payments, the supply store offers a 2% discount on bills paid with 10 days. Please calculate the effective interest rate the store offers its buyers for giving up 20 days of free credit.
- Suppose you borrowed $5,000 for 3 years at an APR rate of 8%. Create an amortization table for this loan.
- Home Depot mailed to some of its customers a coupon entitling them to either a 10% discount on their next purchase or two years of free credit. Under what conditions would you be indifferent between the two options? (Hint: the answer does not depend on the amount purchased.)
- A farm firm has a mortgage loan for $150,000 at an APR rate of 5%. The term of the loan is 15 years and the payments equal $14,451. Cash flow problems from reduced farm income leaves the firm only able to pay $10,000 on this loan. What would the new term equal if the lender allowed the borrower to repay over a longer term?
Supplemental Materials
The refinancing problem described in this chapter can be more
complicated. What if not only the new and old APR loan rate were
different but also the term and the amount refinanced? Let
rO and rN equal the APR on
the old and new loans respectively. Let’s assume that the new loan
included not only the refinanced loan L0 but
also an additional amount equal to  L0.
Also assume that the term on the old loan is
mnO compared to the term on the new loan,
mnN. We want to know if the borrower should
refinance. The IRR used for calculating the NPVs for the new and
old loans is r.
L0.
Also assume that the term on the old loan is
mnO compared to the term on the new loan,
mnN. We want to know if the borrower should
refinance. The IRR used for calculating the NPVs for the new and
old loans is r.
Recall that if the IRR is also the reinvestment rate, then an investment’s NPV is not affected by changing its size and term. Therefore, we can determine if the borrower should refinance by comparing the NPVs on the old and new (refinanced) loan.
Assume for the moment that we know the points charged to refinance a loan and we want to know our loan payment for the refinanced loan. Using the notation already defined, we solve the problem by revising equation (16.21a) and write the revised equation as:
(16.i)
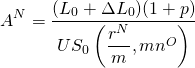
The loan payment for the original (old) loan, for which there are no points charged, can be written as:
(16.ii)
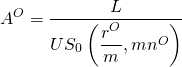
At this point,we make a critical assumption; namely, that funds are reinvested at the defender’s IRR, which allows us to write the NPVs for the new and old loans as:
(16.iii)
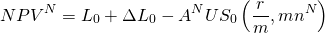
and
(16.iv)
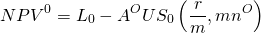
If the points charged make the two loans equal in NPV, then we can equate equations (16.iii) and (16.iv) and solve for the break-even points:
(16.v)
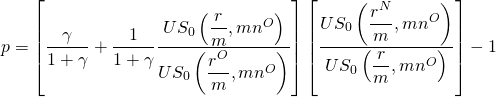
Where 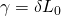 .
Note that if
.
Note that if  = 0" title="Rendered by QuickLaTeX.com" height="18" width="174"
style="vertical-align: -5px;"> and
nO = nN,
equation (16.v) reduces to Equation \ref{16.22}. Therefore,
equation (16.v) allows us to find break-even points in general,
even if the interest rates, term, and size of the refinanced loans
are different compared to the loan being refinanced.
= 0" title="Rendered by QuickLaTeX.com" height="18" width="174"
style="vertical-align: -5px;"> and
nO = nN,
equation (16.v) reduces to Equation \ref{16.22}. Therefore,
equation (16.v) allows us to find break-even points in general,
even if the interest rates, term, and size of the refinanced loans
are different compared to the loan being refinanced.


