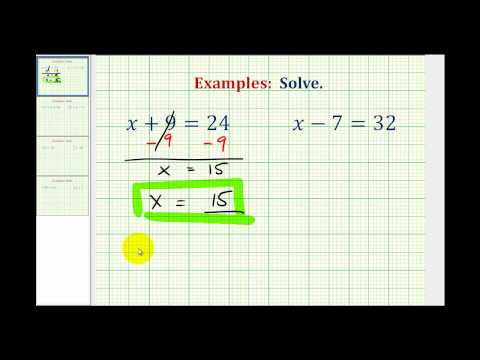
2.15: Solving Single-Step Equations
- Page ID
- 45775
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Outcome
- Use the addition, subtraction, multiplication, and division properties to solve single-step equations
We will begin solving equations below, but first we need to understand what a solution to an equation looks like. The purpose in solving an equation is to find the value or values of the variable that make each side of the equation the same — it is the answer to the puzzle.
Solution of an Equation
A solution of an equation is a value of a variable that makes a true statement when substituted into the equation.
Determine whether a number is a solution to an equation.
- Substitute the number for the variable in the equation.
- Simplify the expressions on both sides of the equation.
- Determine whether the resulting equation is true.
- If it is true, the number is a solution.
- If it is not true, the number is not a solution.
In the following example, we will show how to determine whether a number is a solution to an equation that contains addition and subtraction. You can use this idea to check your work later when you are solving equations.
EXAMPLE
Determine whether \(y=\Large\frac{3}{4}\) is a solution for \(4y+3=8y\).
Solution:
| \(4y+3=8y\) | |
| Substitute \(\color{red}{\Large\frac{3}{4}}\) for \(y\) | \(4(\color{red}{\Large\frac{3}{4}}\normalsize)+3\stackrel{\text{?}}{=}8(\color{red}{\Large\frac{3}{4}})\) |
| Multiply. | \(3+3\stackrel{\text{?}}{=}6\) |
| Add. | \(6=6\quad\checkmark\) |
Since \(y=\Large\frac{3}{4}\) results in a true equation, \(\Large\frac{3}{4}\) is a solution to the equation \(4y+3=8y\).
Now it is your turn to determine whether a fraction is the solution to an equation.
TRY IT
Let’s use a model to help understand how the process of solving an equation is like solving a puzzle. An envelope represents the variable – since its contents are unknown – and each counter represents one.
Suppose a desk has an imaginary line dividing it in half. We place three counters and an envelope on the left side of desk, and eight counters on the right side of the desk. Both sides of the desk have the same number of counters, but some counters are hidden in the envelope. Can you tell how many counters are in the envelope?
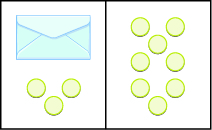
What steps are you taking in your mind to figure out how many counters are in the envelope? Perhaps you are thinking “I need to remove the \(3\) counters from the left side to get the envelope by itself. Those \(3\) counters on the left match with \(3\) on the right, so I can take them away from both sides. That leaves five counters on the right, so there must be \(5\) counters in the envelope.”
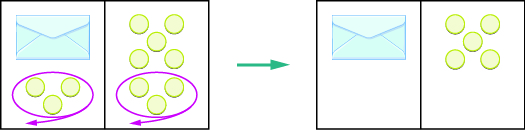
What algebraic equation is modeled by this situation? Each side of the desk represents an expression and the center line takes the place of the equal sign. We will call the contents of the envelope \(x\), so the number of counters on the left side of the desk is \(x+3\). On the right side of the desk are \(8\) counters. We are told that \(x+3\) is equal to \(8\) so our equation is \(x+3=8\).

\(x+3=8\)
Let’s write algebraically the steps we took to discover how many counters were in the envelope.
| \(x+3=8\) | |
| First, we took away three from each side. | \(x+3\color{red}{--3}=8\color {red}{--3}\) |
| Then we were left with five. | \(x=5\) |
Now let’s check our solution. We substitute \(5\) for \(x\) in the original equation and see if we get a true statement.
\(x+3=8\)
\(\color{red}{5}+3=8\)
\(8=8\quad\checkmark\) Our solution is correct. Five counters in the envelope plus three more equals eight.
example
Write an equation modeled by the envelopes and counters, and then solve the equation:
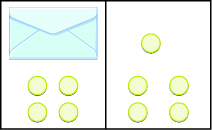
Solution
| On the left, write \(x\) for the contents of the envelope, add the \(4\) counters, so we have \(x+4\). | \(x+4\) |
| On the right, there are \(5\) counters. | \(5\) |
| The two sides are equal. | \(x+4=5\) |
| Solve the equation by subtracting \(4\) counters from each side. |
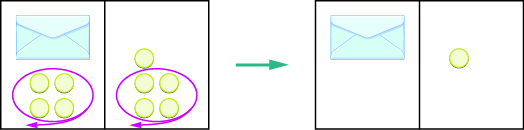
We can see that there is one counter in the envelope. This can be shown algebraically as:
\(x+4=5\)
\(x+4\color{red}{--4}=5\color{red}{--4}\)
\(x=1\)
Substitute \(1\) for \(x\) in the equation to check.
\(x+4=5\)
\(\color{red}{1}+4=5\)
\(5=5\quad\checkmark\)
Since \(x=1\) makes the statement true, we know that \(1\) is indeed a solution.
try it
Write the equation modeled by the envelopes and counters, and then solve the equation:
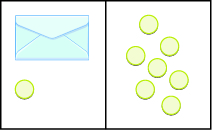
[reveal-answer q=”7845″]Show Answer[/reveal-answer]
[hidden-answer a=”7845″]
\(x+1=7\)
\(x=6\)
[/hidden-answer]
Write the equation modeled by the envelopes and counters, and then solve the equation:
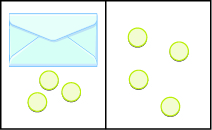
[reveal-answer q=”9034″]Show Answer[/reveal-answer]
[hidden-answer a=”9034″]
\(x+3=4\)
\(x=1\)
[/hidden-answer]
Our puzzle has given us an idea of what we need to do to solve an equation. The goal is to isolate the variable by itself on one side of the equation. In the previous examples, we used the Subtraction Property of Equality, which states that when we subtract the same quantity from both sides of an equation, we still have equality.
Subtraction Property of Equality
For all real numbers \(a,b\), and \(c\), if \(a=b\), then \(a-c=b-c\).
In all the equations we have solved so far, a number was added to the variable on one side of the equation. We used subtraction to “undo” the addition in order to isolate the variable.
But suppose we have an equation with a number subtracted from the variable, such as \(x - 5=8\). We want to isolate the variable, so to “undo” the subtraction we will add the number to both sides.
We use the Addition Property of Equality, which says we can add the same number to both sides of the equation without changing the equality. Notice how it mirrors the Subtraction Property of Equality.
Addition Property of Equality
For all real numbers \(a,b\), and \(c\), if \(a=b\), then \(a+c=b+c\).
When you add or subtract the same quantity from both sides of an equation, you still have equality.
We introduced the Subtraction Property of Equality earlier by modeling equations with envelopes and counters. The image below models the equation \(x+3=8\).
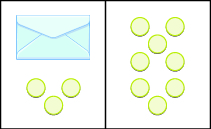
The goal is to isolate the variable on one side of the equation. So we “took away” \(3\) from both sides of the equation and found the solution \(x=5\).
Some people picture a balance scale, as in the image below, when they solve equations.
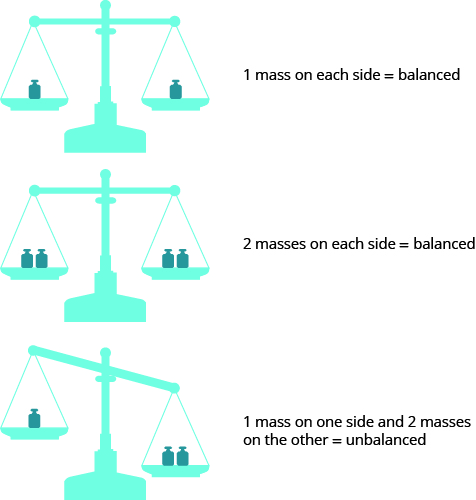
The quantities on both sides of the equal sign in an equation are equal, or balanced. Just as with the balance scale, whatever you do to one side of the equation you must also do to the other to keep it balanced.
In the following examples we review how to use Subtraction and Addition Properties of Equality to solve equations. We need to isolate the variable on one side of the equation. You can check your solutions by substituting the value into the original equation to make sure you have a true statement.
EXAMPLE
Solve: \(x+11=-3\)
[reveal-answer q=”190834″]Show Answer[/reveal-answer]
[hidden-answer a=”190834″]
Solution:
To isolate \(x\), we undo the addition of \(11\) by using the Subtraction Property of Equality.
| \(x+11=-3\) | ||
| Subtract 11 from each side to “undo” the addition. | \(x+11\color{red}{-11}=-3\color{red}{-11}\) | |
| Simplify. | \(x=-14\) | |
| Check: | \(x+11=-3\) | |
| Substitute \(x=-14\). | \(\color{red}{-14}+11\stackrel{\text{?}}{=}-3\) | |
| \(-3=-3\quad\checkmark\) | ||
Since \(x=-14\) makes \(x+11=-3\) a true statement, we know that it is a solution to the equation.
[/hidden-answer]
Now you can try solving an equation that requires using the addition property.
TRY IT
In the original equation in the previous example, \(11\) was added to the \(x\), so we subtracted \(11\) to “undo” the addition. In the next example, we will need to “undo” subtraction by using the Addition Property of Equality.
EXAMPLE
Solve: \(m - 4=-5\)
[reveal-answer q=”604060″]Show Answer[/reveal-answer]
[hidden-answer a=”604060″]
Solution:
| \(m-4=-5\) | ||
| Add 4 to each side to “undo” the subtraction. | \(m-4\color{red}{+4}=-5\color{red}{+4}\) | |
| Simplify. | \(m=-1\) | |
| Check: | \(m-4=-5\) | |
| Substitute \(m=-1\). | \(\color{red}{-1}+4\stackrel{\text{?}}{=}-5\) | |
| \(-5=-5\quad\checkmark\) | ||
| The solution to \(m - 4=-5\) is \(m=-1\) | ||
[/hidden-answer]
Now you can try using the addition property to solve an equation.
TRY IT
In the following video, we present more examples of solving equations using the addition and subtraction properties.
You may encounter equations that contain fractions or decimals — especially in financial applications — so let’s practice solving those in the following problems.
TRY IT
TRY IT
[ohm_question]156990[/ohm_question]
All of the equations we have solved so far have been of the form \(x+a=b\) or \(x-a=b\). We were able to isolate the variable by adding or subtracting the constant term. Now we’ll see how to solve equations that involve division.
We will model an equation with envelopes and counters.
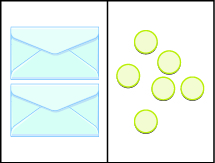
Here, there are two identical envelopes that contain the same number of counters. Remember, the left side of the workspace must equal the right side, but the counters on the left side are “hidden” in the envelopes. So how many counters are in each envelope?
To determine the number, separate the counters on the right side into \(2\) groups of the same size. So \(6\) counters divided into \(2\) groups means there must be \(3\) counters in each group (since \(6\div2=3\)).
What equation models the situation shown in the figure below? There are two envelopes, and each contains \(x\) counters. Together, the two envelopes must contain a total of \(6\) counters. So the equation that models the situation is \(2x=6\).
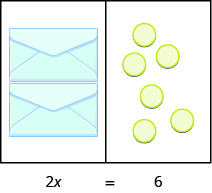
We can divide both sides of the equation by \(2\) as we did with the envelopes and counters.
\(\Large{\frac{2x}{\color{red}{2}}=\frac{6}{\color{red}{2}}}\)
\(x=3\)
We found that each envelope contains \(\text{3 counters.}\) Does this check? We know \(2\cdot 3=6\), so it works. Three counters in each of two envelopes does equal six.
Another example is shown below.
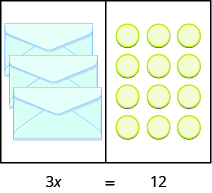
Now we have \(3\) identical envelopes and \(\text{12 counters.}\) How many counters are in each envelope? We have to separate the \(\text{12 counters}\) into \(\text{3 groups.}\) Since \(12\div 3=4\), there must be \(\text{4 counters}\) in each envelope.
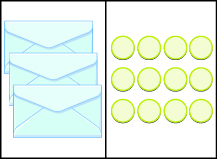
The equation that models the situation is \(3x=12\). We can divide both sides of the equation by \(3\).
\(\Large{\frac{3x}{\color{red}{3}}=\frac{12}{\color{red}{3}}}\)
\(x=4\)
Does this check? It does because \(3\cdot 4=12\).
Division Property of Equality
For all real numbers \(a,b,c\), and \(c\ne 0\), if \(a=b\), then \(\Large\frac{a}{c}\normalsize =\Large\frac{b}{c}\).
Stated simply, when you divide both sides of an equation by the same quantity, you still have equality.
Remember, the goal is to “undo” the operation on the variable. In the example below the variable is multiplied by \(4\), so we will divide both sides by \(4\) to “undo” the multiplication.
example
Solve: \(4x=-28\)
Solution:
To solve this equation, we use the Division Property of Equality to divide both sides by \(4\).
| \(4x=-28\) | |
| Divide both sides by 4 to undo the multiplication. | \(\Large\frac{4x}{\color{red}4}\normalsize =\Large\frac{-28}{\color{red}4}\) |
| Simplify. | \(x =-7\) |
| Check your answer. | \(4x=-28\) |
| Let \(x=-7\). Substitute \(-7\) for x. | \(4(\color{red}{-7})\stackrel{\text{?}}{=}-28\) |
| \(-28=-28\) |
Since this is a true statement, \(x=-7\) is a solution to \(4x=-28\).
Now you can try to solve an equation that requires division and includes negative numbers.
try it
Now, consider the equation \(\Large\frac{x}{4}\normalsize=3\). We want to know what number divided by \(4\) gives \(3\). So to “undo” the division, we will need to multiply by \(4\). The Multiplication Property of Equality will allow us to do this. This property says that if we start with two equal quantities and multiply both by the same number, the results are equal.
Multiplication Property of Equality
For all real numbers \(a,b,c\), if \(a=b\), then \(ac=bc\).
Stated simply, when you multiply both sides of an equation by the same quantity, you still have equality.
Previously we learned how to “undo” multiplication by dividing. How do you think we “undo” division?
Next, we will show an example that requires us to use multiplication to undo division.
example
Solve: \(\Large\frac{a}{-7}\normalsize =-42\)
[reveal-answer q=”399032″]Show Answer[/reveal-answer]
[hidden-answer a=”399032″]
Solution:
Here \(a\) is divided by \(-7\). We can multiply both sides by \(-7\) to isolate \(a\).
| \(\Large\frac{a}{-7}\normalsize =-42\) | |
| Multiply both sides by \(-7\). | \(\color{red}{-7}( \Large\frac{a}{-7}\normalsize)=\color{red}{-7}(-42)\)
\(\Large\frac{-7a}{-7}\normalsize=294\) |
| Simplify. | \(a=294\) |
| Check your answer. | \(\Large\frac{a}{-7}\normalsize=-42\) |
| Let \(a=294\). | \(\Large\frac{\color{red}{294}}{-7}\normalsize\stackrel{\text{?}}{=}-42\) |
| \(-42=-42\quad\checkmark\) |
[/hidden-answer]
Now see if you can solve a problem that requires multiplication to undo division. Recall the rules for multiplying two negative numbers — two negatives give a positive when they are multiplied.
try it
As you begin to solve equations that require several steps you may find that you end up with an equation that looks like the one in the next example, with a negative variable. As a standard practice, it is good to ensure that variables are positive when you are solving equations. The next example will show you how.
example
Solve: \(-r=2\)
[reveal-answer q=”388033″]Show Answer[/reveal-answer]
[hidden-answer a=”388033″]
Solution:
Remember \(-r\) is equivalent to \(-1r\).
| \(-r=2\) | |
| Rewrite \(-r\) as \(-1r\). | \(-1r=2\) |
| Divide both sides by \(-1\). | \(\Large\frac{-1r}{\color{red}{-1}}\normalsize =\Large\frac{2}{\color{red}{-1}}\) |
| Simplify. | \(r=-2\) |
| Check. | \(-r=2\) |
| Substitute \(r=-2\) | \(-(\color{red}{-2})\stackrel{\text{?}}{=}2\) |
| Simplify. | \(2=2\quad\checkmark\) |
[/hidden-answer]
Now you can try to solve an equation with a negative variable.
try it
The next video includes examples of using the division and multiplication properties to solve basic equations.