1.5: Convert Between Decimals and Fractions
- Page ID
- 45764
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning OUTCOME
- Convert decimals to fractions and fractions to decimals
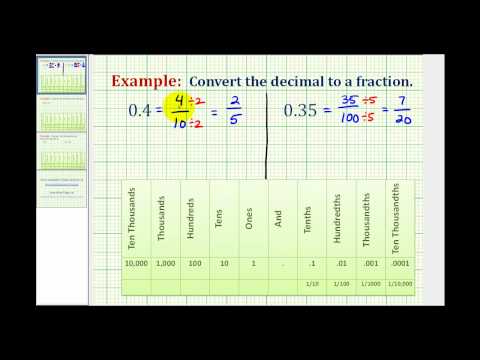
We often need to rewrite decimals as fractions or mixed numbers. Let’s go back to that lunch order to see how we can convert decimal numbers to fractions. We know that \($5.03\) means \(5\) dollars and \(3\) cents. Since there are \(100\) cents in one dollar, \(3\) cents means \({\Large\frac{3}{100}}\) of a dollar, so \(0.03={\Large\frac{3}{100}}\).
We convert decimals to fractions by identifying the place value of the farthest right digit. In the decimal \(0.03\), the \(3\) is in the hundredths place, so \(100\) is the denominator of the fraction equivalent to \(0.03\).
\(0.03={\Large\frac{3}{100}}\)
For our \($5.03\) lunch, we can write the decimal \(5.03\) as a mixed number.
\(5.03=5{\Large\frac{3}{100}}\)
Notice that when the number to the left of the decimal is zero, we get a proper fraction. When the number to the left of the decimal is not zero, we get a mixed number.
Convert a decimal to a fraction or mixed number
- Look at the number to the left of the decimal.
- If it is zero, the decimal converts to a proper fraction.
- If it is not zero, the decimal converts to a mixed number.
- Write the whole number.
- Determine the place value of the final digit.
- Write the fraction.
- numerator—the ‘numbers’ to the right of the decimal point
- denominator—the place value corresponding to the final digit
- Simplify the fraction, if possible.
example
Write each of the following decimal numbers as a fraction or a mixed number:
- \(4.09\)
- \(3.7\)
- \(-0.286\)
Solution:
| 1. | |
| \(4.09\) | |
| There is a \(4\) to the left of the decimal point.
Write “\(4\)” as the whole number part of the mixed number. |
 |
| Determine the place value of the final digit. |  |
| Write the fraction.
Write \(9\) in the numerator as it is the number to the right of the decimal point. |
 |
| Write \(100\) in the denominator as the place value of the final digit, \(9\), is hundredth. | \(4{\Large\frac{9}{100}}\) |
| The fraction is in simplest form. | So, \(4.09=4{\Large\frac{9}{100}}\) |
Did you notice that the number of zeros in the denominator is the same as the number of decimal places?
| 2. | |
| \(3.7\) | |
| There is a \(3\) to the left of the decimal point.
Write “\(3\)” as the whole number part of the mixed number. |
 |
| Determine the place value of the final digit. |  |
| Write the fraction.
Write \(7\) in the numerator as it is the number to the right of the decimal point. |
 |
| Write \(10\) in the denominator as the place value of the final digit, \(7\), is tenths. | \(3{\Large\frac{7}{10}}\) |
| The fraction is in simplest form. | So, \(3.7=3{\Large\frac{7}{10}}\) |
| 3. | |
| \(−0.286\) | |
| There is a \(0\) to the left of the decimal point.
Write a negative sign before the fraction. |
 |
| Determine the place value of the final digit and write it in the denominator. |  |
| Write the fraction.
Write \(286\) in the numerator as it is the number to the right of the decimal point. Write \(1,000\) in the denominator as the place value of the final digit, \(6\), is thousandths. |
\(-{\Large\frac{286}{1000}}\) |
| We remove a common factor of \(2\) to simplify the fraction. | \(-{\Large\frac{143}{500}}\) |
try it
[ohm_question]146573[/ohm_question]
[ohm_question]146574[/ohm_question]
[ohm_question]146575[/ohm_question]
In the next video example, we who how to convert a decimal into a fraction.
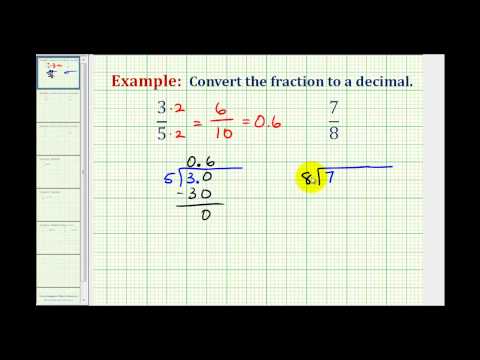
Now we will do the reverse—convert fractions to decimals. Remember that the fraction bar indicates division. So \({\Large\frac{4}{5}}\) can be written \(4\div 5\) or \(5\overline{)4}\). This means that we can convert a fraction to a decimal by treating it as a division problem.
Convert a Fraction to a Decimal
To convert a fraction to a decimal, divide the numerator of the fraction by the denominator of the fraction.
The next decimal shows how to dived a numerator by a denominator using long division, but you can always use a calculator if it’s allowed in your class.
example
Write the fraction \({\Large\frac{3}{4}}\) as a decimal.
Solution
| A fraction bar means division, so we can write the fraction \(\Large\frac{3}{4}\) using division. | 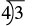 |
| Divide. | 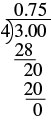 |
| So the fraction \({\Large\frac{3}{4}}\) is equal to \(0.75\) |
try it
[ohm_question]146253[/ohm_question]
The following video contains an example of how to write a fraction as a decimal.
example
Write the fraction \(-{\Large\frac{7}{2}}\) as a decimal.
[reveal-answer q=”746734″]Show Answer[/reveal-answer]
[hidden-answer a=”746734″]
Solution
| The value of this fraction is negative. After dividing, the value of the decimal will be negative. We do the division ignoring the sign, and then write the negative sign in the answer. | \(-{\Large\frac{7}{2}}\) |
| Divide \(7\) by \(2\) | 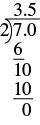 |
| So, | \(-{\Large\frac{7}{2}}=-3.5\). |
[/hidden-answer]
try it
[ohm_question]146257[/ohm_question]
It is useful to convert between fractions and decimals when we need to add or subtract numbers in different forms. To add a fraction and a decimal, for example, we would need to either convert the fraction to a decimal or the decimal to a fraction.
example
Simplify: \({\Large\frac{7}{8}}+6.4\)
[reveal-answer q=”422720″]Show Answer[/reveal-answer]
[hidden-answer a=”422720″]
Solution
| \({\Large\frac{7}{8}}+6.4\) | ||
| Change \(\frac{7}{8}\) to a decimal. |  |
\(0.875+6.4\) |
| Add. | \(7.275\) |
[/hidden-answer]
try it
[ohm_question]146261[/ohm_question]
[ohm_question]146263[/ohm_question]