Skip to main content
Business LibreTexts

14.5: The Phillips Curve

  1. Last updated
  2. Save as PDF
  • Page ID
    47509

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

    Learning Objectives

    • Explain the Phillips curve, noting its impact on the theories of Keynesian economics
    • Demonstrate how the Phillips Curve can be derived from the aggregate supply curve

    The Discovery of the Phillips Curve

    In the 1950s, A.W. Phillips, an economist at the London School of Economics, was studying 60 years of data for the British economy and he discovered an apparent inverse (or negative) relationship between unemployment and wage inflation.  Subsequently, the finding was extended to the relationship between unemployment and price inflation, which became known as the Phillips Curve. Why was there an trade-off between unemployment and inflation?

    The original Keynesian view using the AD-AS model was that AS was “L”-shaped. At any level of GDP below potential, changes in aggregate demand were thought to have no effect on the price level, only on GDP. Only when GDP reached potential would changes in aggregate demand affect prices, but not GDP. You can see this in the original Keynesian AD-AS model, Figure 1, which we first presented in the module on Keynesian Economics.

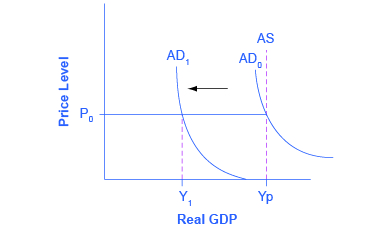
    Keynesian view of the AS-AD model shows that with a horizontal AS, a decrease in demand leads to a decrease in output, but no decrease in prices.
    Figure 1. The Pure Keynesian AD–AS Model. The Keynesian View of the AD–AS Model uses an AS curve which is horizontal at levels of output below potential and vertical at potential output. Thus, changes in AD only affect GDP when below potential output, but only affect the price level when at potential output.

    Most Keynesian economists today have a more nuanced view of the AS curve. When the economy is far from potential GDP, changes in AD mostly affect output but not the price level. When the economy is closer to potential GDP, changes in AD affect output and the price level. And when the economy is at or beyond potential GDP changes in AD only affect the price level.  This yields the more curved AS that we are familiar with, shown in Figure 2.

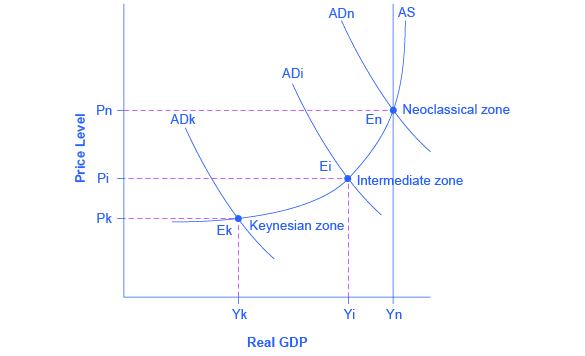
    The graph shows three aggregate demand curves to represent different zones: the Keynesian zone, the intermediate zone, and the neoclassical zone. The Keynesian zone is farthest to the left as well as the lowest; the intermediate zone is the center of the three curves; the neoclassical is farthest to the right as well as the highest.
    Figure 2. Modern Keynesian View of the Aggregate Supply Curve. Near the equilibrium Ek, in the Keynesian zone at the far left of the AS curve, small shifts in AD, either to the right or the left, will affect the output level Yk, but will not much affect the price level. In the Keynesian zone, AD largely determines the quantity of output. Near the equilibrium En, in the neoclassical zone, at the far right of the AS curve, small shifts in AD, either to the right or the left, will have relatively little effect on the output level Yn, but instead will have a greater effect on the price level.

    So where does that leave us with the Phillips Curve? Keynesian theory implied that during a recession, when GDP was below potential and unemployment was high, inflationary pressures would be low. Alternatively, when the level of output is at or even pushing beyond potential GDP, the economy is at greater risk for inflation. This yields the Phillips Curve relationship.

    Figure 3 shows a theoretical Phillips curve, and the following feature shows how the pattern appears for the United States.

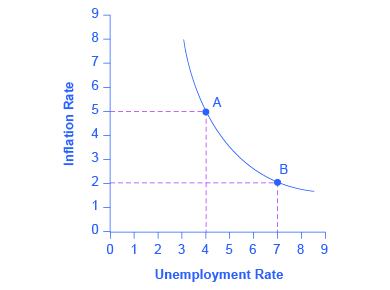
    The graph provides a visual representation of the Phillips curve with a downward-sloping curve.
    Figure 3. A Keynesian Phillips Curve Tradeoff between Unemployment and Inflation. A Phillips curve illustrates a tradeoff between the unemployment rate and the inflation rate; if one is higher, the other must be lower. For example, point A illustrates an inflation rate of 5% and an unemployment rate of 4%. If the government attempts to reduce inflation to 2%, then it will experience a rise in unemployment to 7%, as shown at point B.

    Try It

    https://assessments.lumenlearning.co...sessments/7659
    https://assessments.lumenlearning.co...sessments/7660

    The PHILLIPS CURVE FOR THE UNITED STATES

    Step 1. Go to this website to see the 2005 Economic Report of the President.

    Step 2. Scroll down and locate Table B-63 in the Appendices. This table is titled “Changes in special consumer price indexes, 1960–2004.”

    Step 3. Download the table in Excel by selecting the XLS option and then selecting the location in which to save the file.

    Step 4. Open the downloaded Excel file.

    Step 5. View the third column (labeled “Year to year”). This is the inflation rate, measured by the percentage change in the Consumer Price Index.

    Step 6. Return to the website and scroll to locate the Appendix Table B-42 “Civilian unemployment rate, 1959–2004.

    Step 7. Download the table in Excel.

    Step 8. Open the downloaded Excel file and view the second column. This is the overall unemployment rate.

    Step 9. Using the data available from these two tables, plot the Phillips curve for 1960–69, with unemployment rate on the x-axis and the inflation rate on the y-axis. Your graph should look like Figure 4.

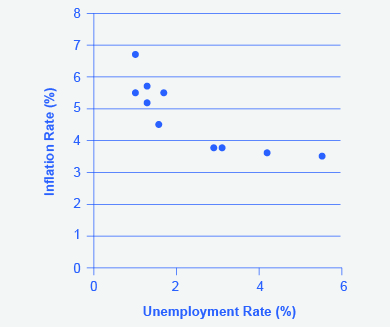
    The Phillips Curve shows a clear negative relationship between the unemployment rate and the inflation rate over the period 1960-69.
    Figure 4. The Phillips Curve from 1960–1969. This chart shows the negative relationship between unemployment and inflation.

    Step 10. Plot the Phillips curve for 1960–1979. What does the graph look like? Do you still see the tradeoff between inflation and unemployment? Your graph should look like Figure 5.

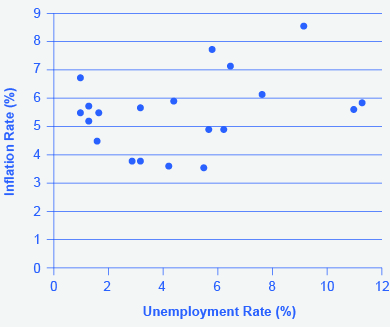
    The tradeoff between unemployment and inflation appeared to break down during the 1970s as the Phillips Curve shifted out to the right, meaning a given unemployment rate corresponds to a variety of rates of inflation and vice versa.
    Figure 5. U.S. Phillips Curve, 1960–1979. The tradeoff between unemployment and inflation appeared to break down during the 1970s as the Phillips Curve shifted out to the right.

    Over this longer period of time, the Phillips curve appears to have shifted out. There is no longer a tradeoff.

    The Instability of the Phillips Curve

    By the mid-1960s, the Phillips Curve was a key part of Keynesian Economics. The relationship was seen as a policy menu. A nation could choose low inflation and high unemployment, or high inflation and low unemployment, or anywhere in between. Expansionary fiscal and monetary policy could be used to move up the Phillips curve. Contractionary fiscal and monetary policy could be used to move down the Phillips curve. An administration could choose any point on the Phillips Curve as desired.

    Then a curious thing happened. When policymakers tried to exploit the tradeoff between inflation and unemployment, the result was an increase in both inflation and unemployment. What had happened? The Phillips curve shifted, but why? The U.S. economy experienced this pattern in the deep recession from 1973 to 1975, and again in back-to-back recessions from 1980 to 1982. Many nations around the world saw similar increases in unemployment and inflation, and this pattern became known as stagflation. (Recall that stagflation is an unhealthy combination of high unemployment and high inflation.) Perhaps most important, stagflation was a phenomenon that could not be explained by traditional Keynesian economics.

    Try It

    https://assessments.lumenlearning.co...sessments/7657
    https://assessments.lumenlearning.co...sessments/7658

    watch it

    Watch this short video for a summary of the Phillips curve and to learn more about the relationship between inflation and unemployment.

    A link to an interactive elements can be found at the bottom of this page.

    Try It

    These questions allow you to get as much practice as you need, as you can click the link at the top of the first question (“Try another version of these questions”) to get a new set of questions. Practice until you feel comfortable doing the questions.

    [ohm_question]154506-154508-154519-154523[/ohm_question]

    Learning Objectives

    [glossary-page]
    [glossary-term]contractionary fiscal policy: [/glossary-term]
    [glossary-definition]tax increases or cuts in government spending designed to decrease aggregate demand and reduce inflationary pressures [/glossary-definition][glossary-term]expansionary fiscal policy: [/glossary-term][glossary-definition]tax cuts or increases in government spending designed to stimulate aggregate demand and move the economy out of recession[/glossary-definition][glossary-term]Phillips curve:[/glossary-term][glossary-definition]the tradeoff between unemployment and inflation[/glossary-definition][glossary-term]Stagflation:  [/glossary-term][glossary-definition]a simultaneous increase in between unemployment and inflation[/glossary-definition]
    [/glossary-page]

    Contributors and Attributions

    CC licensed content, Original
    • Modification, adaptation, and original content. Provided by: Lumen Learning. License: CC BY: Attribution
    CC licensed content, Shared previously
    All rights reserved content

    14.5: The Phillips Curve is shared under a not declared license and was authored, remixed, and/or curated by LibreTexts.

    1. Back to top
    • Was this article helpful?

    Recommended articles

    1. Article type
      Section or Page
      OER program or Publisher
      Lumen
      Show TOC
      no
    2. Tags
      This page has no tags.