12.4: Prisoner’s Dilemma
- Page ID
- 48459
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Objectives
- Explain the role of game theory in understanding the behavior of oligopolies
Because of the complexity of oligopoly, which is the result of mutual interdependence among firms, there is no single, generally-accepted theory of how oligopolies behave, in the same way that we have theories for all the other market structures. Instead, many economists use game theory, a branch of mathematics that analyzes situations in which players must make decisions and then receive payoffs based on what other players decide to do. Game theory has found widespread applications in the social sciences, as well as in business, law, and military strategy.
A key element of game theory is the concept of Nash equilibrium. The concept was developed by John Nash, an American mathematician who was awarded the 1994 Nobel Prize in economics for this work. A Nash equilibrium occurs when no player has an incentive to change their decision, taking into account what the players have decided and assuming the other players don’t change their decisions. Thus, all players have made an optimal decision, given the decisions of the other players.
The prisoner’s dilemma is a scenario in which the gains from cooperation are larger than the rewards from pursuing self-interest. It applies well to oligopoly. The story behind the prisoner’s dilemma goes like this:
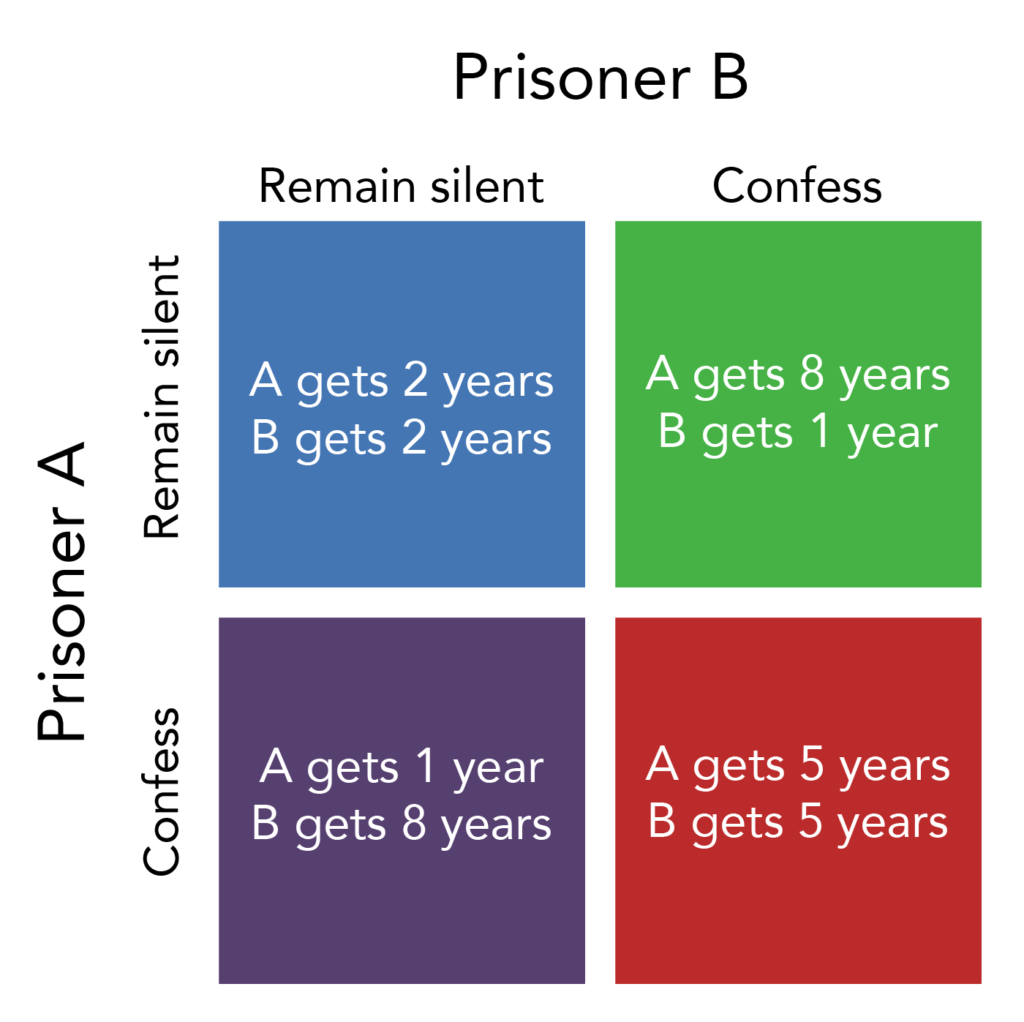
The game theory situation facing the two prisoners is shown in Table 1. To understand the dilemma, first consider the choices from Prisoner A’s point of view. If A believes that B will confess, then A ought to confess, too, so as to not get stuck with the eight years in prison. But if A believes that B will not confess, then A will be tempted to act selfishly and confess, so as to serve only one year. The key point is that A has an incentive to confess regardless of what choice B makes! B faces the same set of choices, and thus will have an incentive to confess regardless of what choice A makes. Confess is considered the dominant strategy or the strategy an individual (or firm) will pursue regardless of the other individual’s (or firm’s) decision. The result is that if prisoners pursue their own self-interest, both are likely to confess, and end up doing a total of 10 years of jail time between them. You should note that this result is a Nash equilibrium.
The game is called a dilemma because if the two prisoners had cooperated by both remaining silent, they would only have had to serve a total of four years of jail time between them. If the two prisoners can work out some way of cooperating so that neither one will confess, they will both be better off than if they each follow their own individual self-interest, which in this case leads straight into longer jail terms.
Oligopoly Version of the Prisoner’s Dilemma
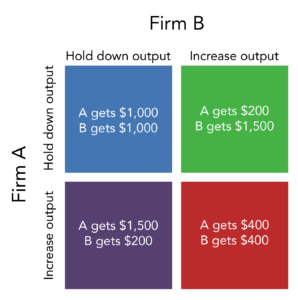
The members of an oligopoly can face a prisoner’s dilemma, also. If each of the oligopolists cooperates in holding down output, then high monopoly profits are possible. Each oligopolist, however, must worry that while it is holding down output, other firms are taking advantage of the high price by raising output and earning higher profits. Table 2 shows the prisoner’s dilemma for a two-firm oligopoly—known as a duopoly. If Firms A and B both agree to hold down output, they are acting together as a monopoly and will each earn $1,000 in profits. However, both firms’ dominant strategy is to increase output, in which case each will earn $400 in profits.
Can the two firms trust each other? Consider the situation of Firm A:
- If A thinks that B will cheat on their agreement and increase output, then A will increase output, too, because for A the profit of $400 when both firms increase output (the bottom right-hand choice in Table 2) is better than a profit of only $200 if A keeps output low and B raises output (the upper right-hand choice in the table).
- If A thinks that B will cooperate by holding down output, then A may seize the opportunity to earn higher profits by raising output. After all, if B is going to hold down output, then A can earn $1,500 in profits by expanding output (the bottom left-hand choice in the table) compared with only $1,000 by holding down output as well (the upper left-hand choice in the table).
Thus, firm A will reason that it makes sense to expand output if B holds down output and that it also makes sense to expand output if B raises output. Again, B faces a parallel set of decisions.
The result of this prisoner’s dilemma is often that even though A and B could make the highest combined profits by cooperating in producing a lower level of output and acting like a monopolist, the two firms may well end up in a situation where they each increase output and earn only $400 each in profits. The following example discusses one cartel scandal in particular.
What is the Lysine cartel?
Lysine, a $600 million-a-year industry, is an amino acid used by farmers as a feed additive to ensure the proper growth of swine and poultry. The primary U.S. producer of lysine is Archer Daniels Midland (ADM), but several other large European and Japanese firms are also in this market. For a time in the first half of the 1990s, the world’s major lysine producers met together in hotel conference rooms and decided exactly how much each firm would sell and what it would charge. The U.S. Federal Bureau of Investigation (FBI), however, had learned of the cartel and placed wire taps on a number of their phone calls and meetings.
From FBI surveillance tapes, following is a comment that Terry Wilson, president of the corn processing division at ADM, made to the other lysine producers at a 1994 meeting in Mona, Hawaii:
The price of lysine doubled while the cartel was in effect. Confronted by the FBI tapes, Archer Daniels Midland pled guilty in 1996 and paid a fine of $100 million. A number of top executives, both at ADM and other firms, later paid fines of up to $350,000 and were sentenced to 24–30 months in prison.
In another one of the FBI recordings, the president of Archer Daniels Midland told an executive from another competing firm that ADM had a slogan that, in his words, had “penetrated the whole company.” The company president stated the slogan this way: “Our competitors are our friends. Our customers are the enemy.” That slogan could stand as the motto of cartels everywhere.
How to Enforce Cooperation
How can parties who find themselves in a prisoner’s dilemma situation avoid the undesired outcome and cooperate with each other? The way out of a prisoner’s dilemma is to find a way to penalize those who do not cooperate.
Perhaps the easiest approach for colluding oligopolists, as you might imagine, would be to sign a contract with each other that they will hold output low and keep prices high. If a group of U.S. companies signed such a contract, however, it would be illegal. Certain international organizations, like the nations that are members of the Organization of Petroleum Exporting Countries (OPEC), have signed international agreements to act like a monopoly, hold down output, and keep prices high so that all of the countries can make high profits from oil exports. Such agreements, however, because they fall in a gray area of international law, are not legally enforceable. If Nigeria, for example, decides to start cutting prices and selling more oil, Saudi Arabia cannot sue Nigeria in court and force it to stop.
Link It Up
Visit the Organization of the Petroleum Exporting Countries website and learn more about its history and how it defines itself.
Because oligopolists cannot sign a legally enforceable contract to act like a monopoly, the firms may instead keep close tabs on what other firms are producing and charging. Alternatively, oligopolists may choose to act in a way that generates pressure on each firm to stick to its agreed quantity of output.
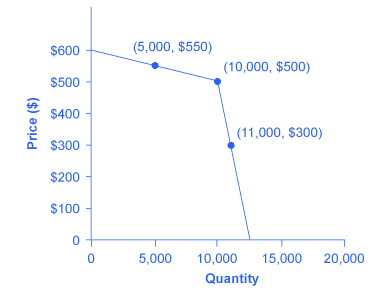
One example of the pressure these firms can exert on one another is the kinked demand curve, in which competing oligopoly firms commit to match price cuts, but not price increases. This situation is shown in Figure 1. Say that an oligopoly airline has agreed with the rest of a cartel to provide a quantity of 10,000 seats on the New York to Los Angeles route, at a price of $500. This choice defines the kink in the firm’s perceived demand curve. The reason that the firm faces a kink in its demand curve is because of how the other oligopolists react to changes in the firm’s price. If the oligopoly decides to produce more and cut its price, the other members of the cartel will immediately match any price cuts—and therefore, a lower price brings very little increase in quantity sold.
If one firm cuts its price to $300, it will be able to sell only 11,000 seats. However, if the airline seeks to raise prices, the other oligopolists will not raise their prices, and so the firm that raised prices will lose a considerable share of sales. For example, if the firm raises its price to $550, its sales drop to 5,000 seats sold. Thus, if oligopolists always match price cuts by other firms in the cartel, but do not match price increases, then none of the oligopolists will have a strong incentive to change prices, since the potential gains are minimal. This strategy can work like a silent form of cooperation, in which the cartel successfully manages to hold down output, increase price, and share a monopoly level of profits even without any legally enforceable agreement.
Many real-world oligopolies, prodded by economic changes, legal and political pressures, and the egos of their top executives, go through episodes of cooperation and competition. If oligopolies could sustain cooperation with each other on output and pricing, they could earn profits as if they were a single monopoly. However, each firm in an oligopoly has an incentive to produce more and grab a bigger share of the overall market; when firms start behaving in this way, the market outcome in terms of prices and quantity can be similar to that of a highly competitive market.
Watch It
Watch this video to review the key characteristics of oligopolies and to see some applications of game theory and collusion.
An interactive or media element has been excluded from this version of the text. You can view it online here: http://pb.libretexts.org/mecon/?p=420
Glossary
[glossary-page][glossary-term]duopoly: [/glossary-term]
[glossary-definition]an oligopoly with only two firms[/glossary-definition][glossary-term]game theory:[/glossary-term]
[glossary-definition]a branch of mathematics that economists use to analyze situations in which players must make decisions and then receive payoffs based on what decisions the other players make[/glossary-definition][glossary-term]kinked demand curve:[/glossary-term]
[glossary-definition]a perceived demand curve that arises when competing oligopoly firms commit to match price cuts, but not price increases[/glossary-definition] [glossary-term]Nash equilibrium:[/glossary-term][glossary-definition]solution to a game-theoretic scenario when no player has an incentive to change their decision, taking into account what the players have decided and assuming the other players don’t change their decisions.[/glossary-definition]
[glossary-term]prisoner’s dilemma:[/glossary-term]
[glossary-definition]a game in which the gains from cooperation are larger than the rewards from pursuing self-interest[/glossary-definition][/glossary-page]
- Oligopoly. Authored by: OpenStax College. Located at: https://cnx.org/contents/vEmOH-_p@4.48:LdUT0FVs@6/Oligopoly. License: CC BY: Attribution. License Terms: Download for free at http://cnx.org/contents/bc498e1f-efe...69ad09a82@4.44
- Game Theory and Oligopoly: Crash Course Economics #26. Provided by: CrashCourse. Located at: https://www.youtube.com/watch?v=PCcVODWm-oY. License: Other. License Terms: Standard YouTube License

