10.15: The Shutdown Point
- Page ID
- 48419
Learning Objectives
- Determine when a firm should continue producing in the short run or at which point it should shutdown
The possibility that a firm may earn losses raises a question: why can the firm not avoid losses by shutting down and not producing at all? The answer is that shutting down can reduce variable costs to zero, but in the short run, the firm has already committed to pay its fixed costs. As a result, if the firm produces a quantity of zero, it would still make losses because it would still need to pay for its fixed costs. Therefore when a firm is experiencing losses, it must face a question: should it continue producing or should it shut down?
As an example, consider the situation of the Yoga Center, which has signed a contract to rent space that costs $10,000 per month. If the firm decides to operate, its marginal costs for hiring yoga teachers is $15,000 for the month. If the firm shuts down, it must still pay the rent, but it would not need to hire labor. Table 1 shows three possible scenarios. In the first scenario, the Yoga Center does not have any clients, and therefore does not make any revenues, in which case it faces losses of $10,000 equal to the fixed costs. In the second scenario, the Yoga Center has clients that earn the center revenues of $12,000 for the month, but ultimately experiences losses of $13,000 due to having to hire yoga instructors to cover the classes. In the third scenario, the Yoga Center earns revenues of $20,000 for the month, but experiences losses of $5,000.
In all three cases, the Yoga Center loses money. In all three cases, when the rental contract expires in the long run, assuming revenues do not improve, the firm should exit this business. In the short run, though, the decision varies depending on the level of losses and whether the firm can cover its variable costs. In scenario 1, the center does not have any revenues, so hiring yoga teachers would increase variable costs and losses, so it should shut down and only incur its fixed costs. In scenario 2, the center’s losses are greater because it does not make enough revenue to cover its variable costs, so it should shut down immediately and only incur its fixed costs. If price is below the minimum average variable cost, the firm would lose less money by shuting down. In contrast, in scenario 3 the revenue that the center can earn is high enough that the losses diminish when it remains open, so the center should remain open in the short run.
| Scenario 1 |
| If the center shuts down now, revenues are zero but it will not incur any variable costs and would only need to pay fixed costs of $10,000. |
profit = total revenue – (fixed costs + variable cost) profit = 0 – $10,000 = –$10,000 |
| Scenario 2 |
| The center earns revenues of $10,000, and variable costs are $15,000. The center should shut down now. |
profit = total revenue – (fixed costs + variable cost) profit = $12,000 – ($10,000 + $15,000) = –$13,000 |
| Scenario 3 |
| The center earns revenues of $20,000, and variable costs are $15,000. The center should continue in business. |
profit = total revenue – (fixed costs + variable cost) profit = $20,000 – ($10,000 + $15,000) = –$5,000 |
Figure 1 illustrates the lesson that remaining open requires the price to exceed the firm’s average variable cost. When the firm is operating below the break-even point, where price equals average cost, it is operating at a loss so it faces two options: continue to produce and lose money or shutdown. Which option is preferable? The one that loses the least money is the best choice.
Let’s return to the raspberry farm example. At a price of $2.00 per pack, as Figure 1(a) illustrates, if the farm stays in operation it will produce at a level of 65 packs of raspberries, and it will make losses of $47.45 (as explained earlier). The alternative would be to shutdown and lose all the fixed costs of $62.00. Since losing $47.45 is preferable to losing $62.00, the profit maximizing (or in this case the loss minimizing) choice is to stay in operation. The key reason is because price is above average variable cost. This means that at the current price the farm can pay all its variable costs, and have some revenue left over to pay some of the fixed costs. So the loss represents the part of the fixed costs the farm can’t pay, which is less than the entire fixed costs. However, if the price declined to $1.50 per pack, as shown in Figure 1(b), and if the firm applied its rule of producing where P = MR = MC, it would produce a quantity of 58. This price is below average variable cost for this level of output. If the farmer cannot pay workers (the variable costs), then it has to shut down. At this price and output, total revenues would be $87 (quantity of 58 times price of $1.50) and total cost would be $162.34 (Fixed cost of $62 and variable cost of $100.34), for overall losses of $75.34. If the farm shuts down, it must pay only its fixed costs of $62, so shutting down is preferable to selling at a price of $1.50 per pack.
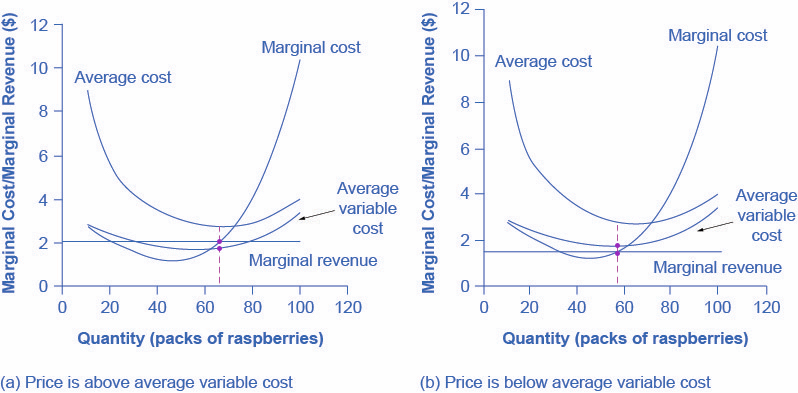
Looking at Table 2, if the price falls below about $1.72, the minimum average variable cost, the firm must shut down.
| Quantity Q | Average Variable Cost AVC | Average Cost AC | Marginal Cost MC |
|---|---|---|---|
| 0 | – | – | – |
| 10 | $2.80 | $9.00 | $2.80 |
| 20 | $2.40 | $5.50 | $2.00 |
| 30 | $2.13 | $4.20 | $1.60 |
| 40 | $1.90 | $3.45 | $1.20 |
| 50 | $1.76 | $3.00 | $1.20 |
| 60 | $1.72 | $2.75 | $1.50 |
| 70 | $1.83 | $2.71 | $2.50 |
| 80 | $2.10 | $2.88 | $4.00 |
| 90 | $2.60 | $3.29 | $6.60 |
| 100 | $3.38 | $4.00 | $10.40 |
| 110 | $4.44 | $5.00 | $15.00 |
| 120 | $5.44 | $5.96 | $31.50 |
The intersection of the average variable cost curve and the marginal cost curve, which shows the price below which the firm would lack enough revenue to cover its variable costs, is called the shutdown point. If the perfectly competitive firm faces a market price above the shutdown point, then the firm is at least covering its average variable costs. At a price above the shutdown point, the firm is also making enough revenue to cover at least a portion of fixed costs, so it should limp ahead even if it is making losses in the short run, since at least those losses will be smaller than if the firm shuts down immediately and incurs a loss equal to total fixed costs. However, if the firm is receiving a price below the price at the shutdown point, then the firm is not even covering its variable costs. In this case, staying open is making the firm’s losses larger, and it should shut down immediately. To summarize, if:
- price < minimum average variable cost, then firm shuts down
- price > minimum average variable cost, then firm stays in business
Short-Run Outcomes for Perfectly Competitive Firms
The average cost and average variable cost curves divide the marginal cost curve into three segments, as Figure 2 shows. At the market price, which the perfectly competitive firm accepts as given, the profit-maximizing firm chooses the output level where price or marginal revenue, which are the same thing for a perfectly competitive firm, is equal to marginal cost: P = MR = MC.
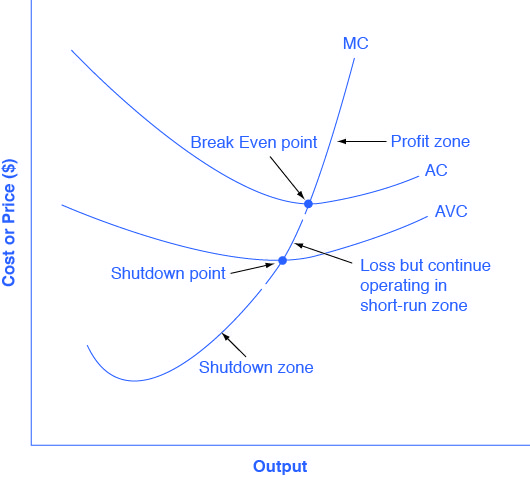
First consider the upper zone, where prices are above the level where marginal cost (MC) crosses average cost (AC) at the zero profit point. At any price above that level, the firm will earn profits in the short run. If the price falls exactly on the break even point where the MC and AC curves cross, then the firm earns zero profits. If a price falls into the zone between the break even point, where MC crosses AC, and the shutdown point, where MC crosses AVC, the firm will be making losses in the short run—but since the firm is more than covering its variable costs, the losses are smaller than if the firm shut down immediately. Finally, consider a price at or below the shutdown point where MC crosses AVC. At any price like this one, the firm will shut down immediately, because it cannot even cover its variable costs.
Marginal Cost and the Firm’s Supply Curve
For a perfectly competitive firm, the marginal cost curve is identical to the firm’s supply curve starting from the minimum point on the average variable cost curve. To understand why this perhaps surprising insight holds true, first think about what the supply curve means. A firm checks the market price and then looks at its supply curve to decide what quantity to produce. Now, think about what it means to say that a firm will maximize its profits by producing at the quantity where P = MC. This rule means that the firm checks the market price, and then looks at its marginal cost to determine the quantity to produce—and makes sure that the price is greater than the minimum average variable cost. In other words, the marginal cost curve above the minimum point on the average variable cost curve becomes the firm’s supply curve.
As we discussed in the module on demand and supply, many of the reasons that supply curves shift relate to underlying changes in costs. For example, a lower price of key inputs or new technologies that reduce production costs cause supply to shift to the right. In contrast, bad weather or added government regulations can add to costs of certain goods in a way that causes supply to shift to the left. We can also interpret these shifts in the firm’s supply curve as shifts of the marginal cost curve. A shift in costs of production that increases marginal costs at all levels of output—and shifts MC upward and to the left—will cause a perfectly competitive firm to produce less at any given market price. Conversely, a shift in costs of production that decreases marginal costs at all levels of output will shift MC downward and to the right and as a result, a competitive firm will choose to expand its level of output at any given price. The following Work It Out feature will walk you through an example.
Exercise: At What Price Should the Firm Continue Producing in the Short Run?
To determine the short-run economic condition of a firm in perfect competition, follow the steps outlined below. Use the data in the table below.
| Table 3. | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Q | P | TFC | TVC | TC | AVC | ATC | MC | TR | Profits |
| 0 | $28 | $20 | $0 | – | – | – | – | – | – |
| 1 | $28 | $20 | $20 | – | – | – | – | – | – |
| 2 | $28 | $20 | $25 | – | – | – | – | – | – |
| 3 | $28 | $20 | $35 | – | – | – | – | – | – |
| 4 | $28 | $20 | $52 | – | – | – | – | – | – |
| 5 | $28 | $20 | $80 | – | – | – | – | – | – |
Step 1. Determine the cost structure for the firm. For a given total fixed costs and variable costs, calculate total cost, average variable cost, average total cost, and marginal cost. Follow the formulas you learned previously in the module on Production. These calculations are listed below.
| Table 4. Cost Structure | |||||||
|---|---|---|---|---|---|---|---|
| Q | P | TFC | TVC | TC (TFC+TVC) | AVC (TVC/Q) | ATC (TC/Q) | MC (TC2−TC1)/ (Q2−Q1) |
| 0 | $28 | $20 | $0 | $20+$0=$20 | – | – | – |
| 1 | $28 | $20 | $20 | $20+$20=$40 | $20/1=$20.00 | $40/1=$40.00 | ($40−$20)/ (1−0)= $20 |
| 2 | $28 | $20 | $25 | $20+$25=$45 | $25/2=$12.50 | $45/2=$22.50 | ($45−$40)/ (2−1)= $5 |
| 3 | $28 | $20 | $35 | $20+$35=$55 | $35/3=$11.67 | $55/3=$18.33 | ($55−$45)/ (3−2)= $10 |
| 4 | $28 | $20 | $52 | $20+$52=$72 | $52/4=$13.00 | $72/4=$18.00 | ($72−$55)/ (4−3)= $17 |
| 5 | $28 | $20 | $80 | $20+$80=$100 | $80/5=$16.00 | $100/5=$20.00 | ($100−$72)/ (5−4)= $28 |
Step 2. Determine the market price that the firm receives for its product. Since the firm in perfect competition is a price taker, the market price is constant. With the given price, calculate total revenue as equal to price multiplied by quantity for all output levels produced. In this example, the given price is $28. You can see that in the second column of the following table.
| Table 5. Constant Prices | ||
|---|---|---|
| Quantity | Price | Total Revenue (P × Q) |
| 0 | $28 | $28×0=$0 |
| 1 | $28 | $28×1=$28 |
| 2 | $28 | $28×2=$56 |
| 3 | $28 | $28×3=$84 |
| 4 | $28 | $28×4=$112 |
| 5 | $28 | $28×5=$140 |
Step 3. Calculate profits as total cost subtracted from total revenue, as Table 6 shows.
| Table 6. Firm Profits | |||
|---|---|---|---|
| Quantity | Total Revenue | Total Cost | Profits (TR−TC) |
| 0 | $0 | $20 | $0−$20=−$20 |
| 1 | $28 | $40 | $28−$40=−$12 |
| 2 | $56 | $45 | $56−$45=$11 |
| 3 | $84 | $55 | $84−$55=$29 |
| 4 | $112 | $72 | $112−$72=$40 |
| 5 | $140 | $100 | $140−$100=$40 |
Step 4. To find the profit-maximizing output level, look at the Marginal Cost column (at every output level produced), as Table 7 shows, and determine where it is equal to the market price. The output level where price equals the marginal cost is the output level that maximizes profits.
| Table 7. Maximizing Profit | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Q | P | TFC | TVC | TC | AVC | ATC | MC | TR | Profits |
| 0 | $28 | $20 | $0 | $20 | – | – | – | $0 | −$20 |
| 1 | $28 | $20 | $20 | $40 | $20.00 | $40.00 | $20 | $28 | −$12 |
| 2 | $28 | $20 | $25 | $45 | $12.50 | $22.50 | $5 | $56 | $11 |
| 3 | $28 | $20 | $35 | $55 | $11.67 | $18.33 | $10 | $84 | $29 |
| 4 | $28 | $20 | $52 | $72 | $13.00 | $18.00 | $17 | $112 | $40 |
| 5 | $28 | $20 | $80 | $100 | $16.40 | $20.40 | $28 | $140 | $40 |
Step 5. Once you have determined the profit-maximizing output level (in this case, output quantity 5), you can look at the amount of profits made (in this case, $40).
Step 6. If the firm is making economic losses, the firm needs to determine whether it produces the output level where price equals marginal revenue and equals marginal cost or it shuts down and only incurs its fixed costs.
Step 7. For the output level where marginal revenue is equal to marginal cost, check if the market price is greater than the average variable cost of producing that output level.
- If P > AVC but P < ATC, then the firm continues to produce in the short-run, making economic losses.
- If P < AVC, then the firm stops producing and only incurs its fixed costs.
In this example, the price of $28 is greater than the AVC ($16.40) of producing 5 units of output, so the firm continues producing.
Key Concepts and Summary
As a perfectly competitive firm produces a greater quantity of output, its total revenue steadily increases at a constant rate determined by the given market price. Profits will be highest (or losses will be smallest) at the quantity of output where total revenues exceed total costs by the greatest amount (or where total revenues fall short of total costs by the smallest amount). Alternatively, profits will be highest where marginal revenue, which is price for a perfectly competitive firm, is equal to marginal cost. If the market price faced by a perfectly competitive firm is above average cost at the profit-maximizing quantity of output, then the firm is making profits. If the market price is below average cost at the profit-maximizing quantity of output, then the firm is making losses.
If the market price is equal to average cost at the profit-maximizing level of output, then the firm is making zero profits. We call the point where the marginal cost curve crosses the average cost curve, at the minimum of the average cost curve, the break-even point. If the market price that a perfectly competitive firm faces is below average variable cost at the profit-maximizing quantity of output, then the firm should shut down operations immediately. If the market price that a perfectly competitive firm faces is above average variable cost, but below average cost, then the firm should continue producing in the short run, but exit in the long run. We call the point where the marginal cost curve crosses the average variable cost curve the shutdown point.
Watch It
This video carefully explains the graphs you need to understand for perfect competition (it moves slowly so feel free to change the speed settings or review the parts you need most). Watch to see how profit is calculated and why firms will eventually leave at the shutdown point.
Try It
These questions allow you to get as much practice as you need, as you can click the link at the top of the first question (“Try another version of these questions”) to get a new set of questions. Practice until you feel comfortable doing the questions.
[ohm_question]155107-155108-155109-155100[/ohm_question]
Learning Objectives
- [glossary-page][glossary-term]break-even point:[/glossary-term]
[glossary-definition]level of output where the marginal cost curve intersects the average cost curve at the minimum point of AC; if the price is at this point, the firm is earning zero economic profits[/glossary-definition][glossary-term]shutdown point:[/glossary-term]
[glossary-definition]level of output where the marginal cost curve intersects the average variable cost curve at the minimum point of AVC; if the price is below this point, the firm should shut down immediately[/glossary-definition][/glossary-page]
Contributors and Attributions
- How Perfectly Competitive Firms Make Output Decisions. Authored by: OpenStax College. Located at: https://cnx.org/contents/XAl2LLVA@7.32:EkZLadKh@7/How-Perfectly-Competitive-Firm#ch08mod02_tab09. License: CC BY: Attribution. License Terms: Download for free at http://cnx.org/content/col11627/latest
- How to calculate profit, loss, marginal cost in a Perfect Competition. Provided by: Economicsfun. Located at: https://www.youtube.com/watch?v=V81gQroEszI. License: Other. License Terms: Standard YouTube License

