6.14: Comparing Nominal and Real GDP
- Page ID
- 47352
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Objectives
- Explain and demonstrate the difference between nominal and real GDP
Comparing Nominal and Real GDP
In the last section, we introduced the difference between real measurements and nominal measurements of the same economic statistic. On this page, we explore this challenging, but important, distinction in more depth.
Table 1 shows U.S. GDP at five-year intervals since 1960 in nominal dollars; that is, GDP measured using the actual market prices prevailing in each stated year. This data is also reflected in the graph shown in Figure 1.
| Table 1. U.S. Nominal GDP (1960-2010) | ||
|---|---|---|
| Year | Nominal GDP (billions of dollars) | 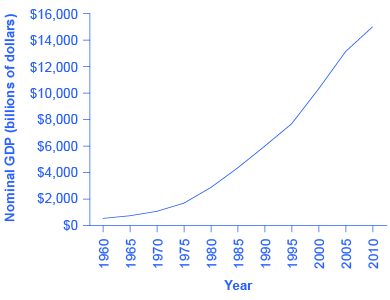 |
If an unwary analyst compared nominal GDP in 1960 to nominal GDP in 2010, it might appear that national output had risen by a factor of nearly twenty-seven over this time. This conclusion comes from the simple growth rate formula (or percentage change formula):
(Final GDP – Initial GDP) / Initial GDP = Growth of Nominal GDP
or
($14,958 – $543) / $543 = 2653%
This conclusion, though, would be highly misleading. Recall that nominal GDP is defined as the quantity of every final good or service produced multiplied by the price at which it was sold, summed up for all goods and services. In other words, nominal GDP is the value of output produced:
We’ll call this the Real-to-Nominal formula.
Watch It
Watch this video to see an example of how inflation can distort our perception of GDP. In this example, we focus on a simplified economy with only one good: apples.
GDP in year one is $1000 and the GDP in year two is $1200. The price for apples in year one was $0.50 per pound, but it rose to $0.55 per pound in year two. We know that the value of apple production increased, but we want to determine the extent to which we are producing more apples (i.e. more quantity of goods and services). Since the value of apples is the price of apples times the quantity produced, we can determine the quantity of apples produced in any year by dividing the value of apples in that year (e.g. $1000 in year one) by the price of apples in that year (e.g. $0.50 in year one):
We can do the same calculation for year two:
The difference in the number of apples produced is 182 lbs. The growth rate (percentage increase) is
Now compare this with the growth in the value of apples:
So, we appeared to be producing 20% more apples, but in reality we were only producing less than half that or 9.1%.
In sum, nominal GDP was $1000 in year one and $1200 in year two, while real GDP was 2000 lbs of apples in year one and 2182 lbs in year two. To compare these GDPs in dollars, you can look at Year Two’s output using Year One’s dollar amount. So
2182 lbs x $0.50 = $1091
Year Two’s real GDP in dollars is $1091. If prices were held constant, the growth in GDP would have been $91, and not the $200 implied by the nominal GDP.
Nominal output is the value of what’s produced, while real output is the quantity of what’s produced (in the previous case, pounds of apples). If we produce more apples we can say our real output has increased.
Now suppose our apply economy from above now produces two goods: apples and xylophones.
| Year | Price of Apples | Quantity of Apples | Value of Apples | Price of Xylophones | Quantity of Xylophones | Value of Xylophones |
| Year One | $0.50 | 2000 lbs | $1,000 | $10 | 100 | $1,000 |
| Year Two | $0.55 | 2182 lbs | $1,200 | $12 | 150 | $1,800 |
It’s easy to compute how much nominal GDP has increased. In year one, the value of apples produced was $1000, and the value of xylophones produced was $1000, so nominal GDP (assuming these are the only two goods in the economy) was $2000. Similarly in year 2, the value of apples produced was $1200, and the value of xylophones produced was $1800, so nominal GDP was $3000. Thus, nominal GDP increased by $1000 (the increase)/$2000 (the nominal GDP in year one)= 50%.
But what has happened to real GDP? Real output of apples has increased from 2000 lbs to 2182 lbs. Real output of xylophones has increased from 100 to 150. How much has real output increased? Can we say that Real GDP has increased from 2100 to 2332 items? The answer is no, because it doesn’t make sense to add apples & xylophones together, since they are used for different purposes and have different values. What we need is a common denominator, which would allow us to compare apples and xylophones. The common denominator economists use for this purpose is price, since price reflects the value of what something is worth.
Remember that we’re using price here as a common denominator to enable us to “add” quantities of apples and xylophones together. But which year’s prices should we use? The answer is arbitrary. We can choose the prices from any year as long as we use them with each year’s quantities. Suppose we choose the set of prices from year one. We use those prices, both in year one and in year two. Thus, real GDP in year one is
But note that real GDP in year two is
In other words, we compute real GDP in every year using the prices that existed in a single year, in this case year 1. That’s why real GDP is often described as being based on “constant dollars” or “year one dollars”.
Plugging in the values from the table above, yields:
In other words real GDP increased by $591/$2000 = 29.6%, which is significantly less than the increase in nominal GDP of 50%.
Why does the distinction between real and nominal GDP matter?
We explained earlier that nominal measures are distorted by the effects of inflation. Thus, nominal GDP inflates the actual quantity of goods and services produced (i.e. real GDP) making it look bigger than it really is. Let’s think of this another way. Real GDP is highly correlated with employment and the standard of living. When real GDP increases, we tend to have more jobs and more goods and services to consume. When businesses need to produce more goods and services, they typically need to hire more workers, which means incomes are up. By contrast, when inflation drives nominal GDP up, there may be no effect on jobs and the standard of living. If businesses are producing the same quantity of goods and services, they don’t need to hire more workers. The same quantity of things just cost more.
Learning Objectives
[glossary-page][glossary-term]nominal value:[/glossary-term]
[glossary-definition] an economic statistic measured using actual market prices; i.e. nominal values are not adjusted for inflation; contrast with real value[/glossary-definition][glossary-term]real-to-nominal formula: [/glossary-term][glossary-definition]the nominal value of some economic variable (e.g. GDP) is the price level times the real value of that economic variable.[/glossary-definition][glossary-term] real value: [/glossary-term][glossary-definition]an economic statistic measured using prices that existed in an earlier year (or period); real values have been adjusted for inflation since that earlier year; contrast with nominal value[/glossary-definition][glossary-term]simple growth rate formula: [/glossary-term][glossary-definition]the growth rate (or percentage change) of any variable X over time is (the value of X in the final period – the value of X in the initial period)/(the value of X in the initial period)[/glossary-definition][/glossary-page]
Contributors and Attributions
- Modification, adaptation, and original content. Provided by: Lumen Learning. License: CC BY: Attribution
- Adjusting Nominal Values to Real Values. Authored by: OpenStax College. Provided by: Rice University. Located at: https://cnx.org/contents/vEmOH-_p@4.44:O3I2vr0L@7/Adjusting-Nominal-Values-to-Re. License: CC BY: Attribution. License Terms: Download for free at http://cnx.org/contents/bc498e1f-efe...69ad09a82@4.44
- Real GDP and nominal GDP. Provided by: Khan Academy. Located at: https://www.khanacademy.org/economics-finance-domain/macroeconomics/gdp-topic/real-nominal-gdp-tutorial/v/real-gdp-and-nominal-gdp. License: CC BY-NC-SA: Attribution-NonCommercial-ShareAlike
- Tracking Real GDP over Time. Authored by: OpenStax College. Located at: https://cnx.org/contents/vEmOH-_p@4.44:q0M-qJRG@7/Tracking-Real-GDP-over-Time. License: CC BY: Attribution. License Terms: Download for free at http://cnx.org/contents/bc498e1f-efe...69ad09a82@4.44

