2.18: Translating Words Into Algebra

Last updated
Save as PDF

Page ID: 45778

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Learning outcome

Translate simple word phrases into math notation

We know there are many operation symbols that are used in algebra. Now, we’ll translate word phrases into algebraic expressions and equations. The symbols and variables we’ve talked about will help us do that. They are summarized below.

Operation	Phrase	Expression
Addition	$a$ plus $b$ the sum of $a$ and $b$ $a$ increased by $b$ $b$ more than $a$ the total of $a$ and $b$ $b$ added to $a$	$a+b$
Subtraction	$a$ minus $b$ the difference of $a$ and $b$ $b$ subtracted from $a$ $a$ decreased by $b$ $b$ less than $a$	$a-b$
Multiplication	$a$ times $b$ the product of $a$ and $b$	$a\cdot b$ , $ab$ , $a\left(b\right)$ , $\left(a\right)\left(b\right)$
Division	$a$ divided by $b$ the quotient of $a$ and $b$ the ratio of $a$ and $b$ $b$ divided into $a$	$a\div b$ , $a/b$ , $\frac{a}{b}$ , $b\overline{)a}$

Look closely at these phrases using the four operations:

the sum of $a$ and $b$
the difference of $a$ and $b$
the product of $a$ and $b$
the quotient of $a$ and $b$

Each phrase tells you to operate on two numbers. Look for the words of and and to find the numbers.

example

Translate each word phrase into an algebraic expression:

1. The difference of $20$ and $4$

2. The quotient of $10x$ and $3$

Solution

1. The key word is difference, which tells us the operation is subtraction. Look for the words of and and to find the numbers to subtract.

The difference of $20$ and $4$

$20$ minus $4$

$20-4$

2. The key word is quotient, which tells us the operation is division.

The quotient of $10x$ and $3$

divide $10x$ by $3$

$10x\div{3}$

This can also be written as $(10x)/3$ or $\frac{10x}{3}$

try it

[ohm_question]146541[/ohm_question]

[ohm_question]143240[/ohm_question]

[ohm_question]143207[/ohm_question]

[ohm_question]146542[/ohm_question]

example

Translate each word phrase into an algebraic expression:

How old will you be in eight years? Let’s say your current age is $y$ .
How old were you seven years ago? This is seven years less than your age now. Let’s say your current age is $9z$ .

[reveal-answer q=”879313″]Show Answer[/reveal-answer]
[hidden-answer a=”879313″]

Solution:

1. Eight more than $y$

The key words are more than. They tell us the operation is addition. More than means “added to”.

Eight more than $y$

Eight added to $y$

$y+8$

2. Seven less than $9z$ .

The key words are less than. They tell us the operation is subtraction. Less than means “subtracted from”.

Seven less than $9z$

Seven subtracted from $9z$

$9z - 7$

[/hidden-answer]

try it

[ohm_question]144907[/ohm_question]

example

Translate each word phrase into an algebraic expression:

1. Five times the sum of $m$ and $n$
2. The sum of five times $m$ and $n$
[reveal-answer q=”888823″]Show Answer[/reveal-answer]
[hidden-answer a=”888823″]

Solution

1. There are two operation words: times tells us to multiply and sum tells us to add. Because we are multiplying $5$ times the sum, we need parentheses around the sum of $m$ and $n$ .

five times the sum of $m$ and $n$

$5(m+n)$

2. To take a sum, we look for the words of and and to see what is being added. Here we are taking the sum of five times $m$ and $n$ .

the sum of five times $m$ and $n$

$5m+n$

Notice how the use of parentheses changes the result. In part 1, we add first and in part 2, we multiply first.

[/hidden-answer]

try it

[ohm_question]144916[/ohm_question]

Watch the video below to better understand how to write algebraic expressions from statements.

Thumbnail for the embedded element "Write Algebraic Expressions from Statements: Form ax+b and a(x+b)"

A YouTube element has been excluded from this version of the text. You can view it online here: http://pb.libretexts.org/afm-2/?p=100

We’ll eventually apply our skills in algebra to solving equations in complex word problems. Usually start by translating a word phrase to an algebraic equation. Remember, an equation has an equal sign between two algebraic expressions. So if we have a sentence that tells us that two phrases are equal, we can translate it into an equation. We look for clue words that mean equals. Some words that translate to the equal sign are:

is equal to
is the same as
is
gives
was
will be

It may be helpful to put a box around the equals word(s) in the sentence to help you focus separately on each phrase. Then translate each phrase into an expression, and write them on each side of the equal sign.

example

Translate the sentence into an algebraic equation: The sum of $6$ and $9$ is $15$ .

Solution
The word is tells us the equal sign goes between 9 and 15.

Locate the “equals” word(s).
Write the = sign.
Translate the words to the left of the equals word into an algebraic expression.
Translate the words to the right of the equals word into an algebraic expression.

try it

[ohm_question]146546[/ohm_question]

example

Translate the sentence into an algebraic equation: Twice the difference of $x$ and $3$ gives $18$ .
[reveal-answer q=”79895″]Show Answer[/reveal-answer]
[hidden-answer a=”79895″]

Solution

Locate the “equals” word(s).
Recognize the key words: twice; difference of …. and ….	Twice means two times.
Translate.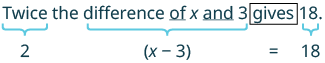
	$2(x-3)=18$

[/hidden-answer]

try it

[ohm_question]146549[/ohm_question]

[ohm_question]146550[/ohm_question]

Thumbnail for the embedded element "Introduction to Variables and Variable Expressions"

A YouTube element has been excluded from this version of the text. You can view it online here: http://pb.libretexts.org/afm-2/?p=100

Now let’s apply our understanding of translating words to algebra in a real world scenario.

example

The height of a rectangular window is $6$ inches less than the width. Let $w$ represent the width of the window. Write an expression for the height of the window.
[reveal-answer q=”704093″]Show Answer[/reveal-answer]
[hidden-answer a=”704093″]

Solution

Write a phrase about the height.	$6$ less than the width
Substitute $w$ for the width.	$6$ less than $w$
Rewrite ‘less than’ as ‘subtracted from’.	$6$ subtracted from $w$
Translate the phrase into algebra.	$w - 6$

[/hidden-answer]

try it

[ohm_question]144917[/ohm_question]

example

Blanca has dimes and quarters in her purse. The number of dimes is $2$ less than $5$ times the number of quarters. Let $q$ represent the number of quarters. Write an expression for the number of dimes.
[reveal-answer q=”365611″]Show Answer[/reveal-answer]
[hidden-answer a=”365611″]

Solution

Write a phrase about the number of dimes.	two less than five times the number of quarters
Substitute $q$ for the number of quarters.	$2$ less than five times $q$
Translate $5$ times $q$ .	$2$ less than $5q$
Translate the phrase into algebra.	$5q - 2$

[/hidden-answer]

try it

[ohm_question]144918[/ohm_question]

In the following video we show more examples of how to write basic algebraic expressions from words, and simplify.

Thumbnail for the embedded element "Write Basic Expressions from Words Modeling Situations"

A YouTube element has been excluded from this version of the text. You can view it online here: http://pb.libretexts.org/afm-2/?p=100

Let’s practice translating sentences into algebraic equations and then solving them.

example

Translate and solve: Three more than $x$ is equal to $47$ .
[reveal-answer q=”989526″]Show Answer[/reveal-answer]
[hidden-answer a=”989526″]

Solution

		Three more than x is equal to $47$ .
Translate.		$x+3=47$
Subtract $3$ from both sides of the equation.		$x+3\color{red}{--3}=47\color{red}{--3}$
Simplify.		$x=44$
We can check. Let $x=44$ .	$x+3=47$
	$44+3=47$
	$47=47\quad\checkmark$

So $x=\text{}44$ is the solution.

[/hidden-answer]

try it

[ohm_question]146551[/ohm_question]

example

Translate and solve: The difference of $y$ and $14$ is $18$ .
[reveal-answer q=”763260″]Show Answer[/reveal-answer]
[hidden-answer a=”763260″]

Solution

		The difference of $y$ and $14$ is $18$ .
Translate.		$y-14=18$
Add $14$ to both sides.		$y-14\color{red}{+14}=18\color{red}{+14}$
Simplify.		$y=32$
We can check. Let $y=32$ .	$y--14=18$
	$32--14=18$
	$18=18\quad\checkmark$

So $y=32$ is the solution.

[/hidden-answer]

try it

[ohm_question]146552[/ohm_question]

[ohm_question]146386[/ohm_question]

In the following video we show more examples of how to translate an equation into words and solve. Note that this is different from the written examples on this page because we start with the mathematical equation then translate it into words.

Thumbnail for the embedded element "Solving Equations Using the Story of x (Part 1)"

A YouTube element has been excluded from this version of the text. You can view it online here: http://pb.libretexts.org/afm-2/?p=100

Exercises

Translate from algebra to words:

$12+14$
$\left(30\right)\left(5\right)$
$64\div 8$
$x-y$

Solution:

$12+14$

$12$ plus $14$

the sum of twelve and fourteen

$\left(30\right)\left(5\right)$

$30$ times $5$

the product of thirty and five

$64\div 8$

$64$ divided by $8$

the quotient of sixty-four and eight

$x-y$

$x$ minus $y$

the difference of $x$ and $y$

TRY IT

An interactive or media element has been excluded from this version of the text. You can view it online here: http://pb.libretexts.org/afm-2/?p=100

What if we are working with expressions that are not equal? An inequality is used in algebra to compare two quantities that may have different values. The number line can help you understand inequalities. Remember that on the number line the numbers get larger as they go from left to right. So if we know that $b$ is greater than $a$ , it means that $b$ is to the right of $a$ on the number line. We use the symbols $\text{<}$ and $\text{>}$ }" title="\text{>}" class="latex mathjax"> for inequalities.

$a<b$ is read $a$ is less than $b$
$a$ is to the left of $b$ on the number line

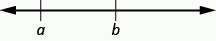
The figure shows a horizontal number line that begins with the letter a on the left then the letter b to its right.
b" title="a>b" class="latex mathjax"> is read $a$ is greater than $b$
$a$ is to the right of $b$ on the number line

The figure shows a horizontal number line that begins with the letter b on the left then the letter a to its right.

The expressions $a<b\text{ and }a>b$ b" title="ab" class="latex mathjax"> can be read from left-to-right or right-to-left, though in English we usually read from left-to-right. In general,

$\begin{array}{l}a<b\text{ is equivalent to }b>a.\text{ For example, }7<11\text{ is equivalent to }11>7.\hfill \\ a>b\text{ is equivalent to }b<a.\text{ For example, }17>4\text{ is equivalent to }4<17.\hfill \end{array}$ a.\text{ For example, }7<11\text{ is equivalent to }11>7.\hfill \\ a>b\text{ is equivalent to }b4\text{ is equivalent to }4<17.\hfill \end{array}" title="\begin{array}{l}a<b\text{ is equivalent to }b>a.\text{ For example, }7<11\text{ is equivalent to }11>7.\hfill \\ a>b\text{ is equivalent to }b 4\text{ is equivalent to }4<17.\hfill \end{array}" class="latex mathjax">

When we write an inequality symbol with a line under it, such as $a\le b$ , it means $a<b$ or $a=b$ . We read this $a$ is less than or equal to $b$ . Also, if we put a slash through an equal sign, $\ne$ , it means not equal.

We summarize the symbols of equality and inequality in the table below.

Algebraic Notation	Say
$a=b$	$a$ is equal to $b$
$a\ne b$	$a$ is not equal to $b$
$a<b$	$a$ is less than $b$
b" title="a>b" class="latex mathjax">	$a$ is greater than $b$
$a\le b$	$a$ is less than or equal to $b$
$a\ge b$	$a$ is greater than or equal to $b$