1.21: Multiplying and Dividing Fractions

Last updated
Save as PDF

Page ID: 45759

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Learning Objectives

Use multiplication and division when evaluating expressions with fractions

Fraction Multiplication

A model may help you understand multiplication of fractions. We will use fraction tiles to model $\frac{1}{2}\cdot \frac{3}{4}$ .

To multiply $\frac{1}{2}$ and $\frac{3}{4}$ , think “I need to find $\frac{1}{2}$ of $\frac{3}{4}$ .”

Start with fraction tiles for three-fourths. To find one-half of three-fourths, we need to divide them into two equal groups. Since we cannot divide the three $\frac{1}{4}$ tiles evenly into two parts, we exchange them for smaller tiles.

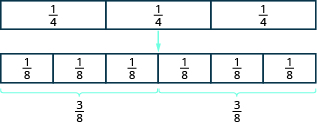
A rectangle is divided vertically into three equal pieces. Each piece is labeled as one fourth. There is a an arrow pointing to an identical rectangle divided vertically into six equal pieces. Each piece is labeled as one eighth. There are braces showing that three of these rectangles represent three eighths.
We see $\frac{6}{8}$ is equivalent to $\frac{3}{4}$ . Taking half of the six $\frac{1}{8}$ tiles gives us three $\frac{1}{8}$ tiles, which is $\frac{3}{8}$ .

Therefore, $\frac{1}{2}\cdot \frac{3}{4}=\frac{3}{8}$

Example

Use a diagram to model $\frac{1}{3}\cdot \frac{2}{5}$

Solution:

You want to find one-third of two-fifths.

First shade in $\frac{2}{5}$ of the rectangle.

A long rectangle is divided into five equal sections with vertical lines. Two of the resulting boxes are shaded blue.
We will take $\frac{1}{3}$ of this $\frac{2}{5}$ , so we heavily shade $\frac{1}{3}$ of the shaded region.

A long rectangle is divided into five equal sections with vertical lines and three equal sections with horizontal lines. There are fifteen resulting boxes and two are shaded dark blue to show the overlap.
Notice that $2$ out of the $15$ pieces are heavily shaded. This means that $\frac{2}{15}$ of the rectangle is heavily shaded.
Therefore, $\frac{1}{3}$ of $\frac{2}{15}$ is $\frac{2}{15}$ , or $\frac{1}{3}\cdot \frac{2}{5}=\frac{2}{15}$

Try it

[ohm_question height=”270″]146020[/ohm_question]

Look at the result we got from the examples above. We found that $\frac{1}{2}\cdot \frac{3}{4}=\frac{3}{8}$ and $\frac{1}{3}\cdot \frac{2}{5}=\frac{2}{15}$ . Do you notice that we could have gotten the same answers by multiplying the numerators and multiplying the denominators?

	$\frac{1}{2}\cdot \frac{3}{4}$	$\frac{1}{3}\cdot \frac{2}{5}$
Multiply the numerators, and multiply the denominators.	$\frac{1}{2}\cdot \frac{3}{4}=\frac{1\cdot 3}{2\cdot 4}$	$\frac{1}{3}\cdot \frac{2}{5}=\frac{1\cdot 2}{3\cdot 5}$
Simplify.	$\frac{3}{8}$	$\frac{2}{15}$

This leads to the definition of fraction multiplication. To multiply fractions, we multiply the numerators and multiply the denominators. Then we write the fraction in simplified form.

Fraction Multiplication

If $a,b,c,\text{ and }d$ are numbers where $b\ne 0\text{ and }d\ne 0$ , then $\Large\frac{a}{b}\cdot \Large\frac{c}{d}=\Large\frac{ac}{bd}$

Example

Multiply, and write the answer in simplified form: $\frac{3}{4}\cdot \frac{1}{5}$
[reveal-answer q=”56385″]Show Answer[/reveal-answer]
[hidden-answer a=”56385″]

Solution:

$\frac{3}{4}\cdot \frac{1}{5}$
Multiply the numerators; multiply the denominators.	$\frac{3\cdot 1}{4\cdot 5}$
Simplify.	$\frac{3}{20}$

There are no common factors, so the fraction is simplified.

[/hidden-answer]

Try It

[ohm_question]146021[/ohm_question]

Note that when multiplying fractions, the properties of positive and negative numbers still apply. It is a good idea to determine the sign of the product as the first step.

The following video provides more examples of how to multiply fractions, and simplify the result.

Thumbnail for the embedded element "Ex 1: Multiply Fractions (Basic)"

A YouTube element has been excluded from this version of the text. You can view it online here: http://pb.libretexts.org/afm-2/?p=60

When multiplying a fraction by an integer, it may be helpful to write the integer as a fraction. Any integer, $a$ , can be written as $\large\frac{a}{1}$ . So, $3=\frac{3}{1}$ , for example.

example

Multiply, and write the answer in simplified form:

$\frac{1}{7}\cdot 56$
$(-20)(\large\frac{12}{5})$

[reveal-answer q=”597781″]Show Answer[/reveal-answer]
[hidden-answer a=”597781″]

Solution:

1.
	$\frac{1}{7}\cdot 56$
Write $56$ as a fraction.	$\frac{1}{7}\cdot \frac{56}{1}$
Determine the sign of the product; multiply.	$\frac{56}{7}$
Simplify.	$8$

2.
	$(-20)(\frac{12}{5})$
Write $−20$ as a fraction.	$\frac{-20}{1}(\frac{12}{5})$
Determine the sign of the product; multiply.	$-\frac{20\cdot 12\cdot}{1\cdot 5}$
Multiply and simplify.	$-\frac{240}{5}=-\frac{2\cdot\color{red}{5}\cdot24}{\color{red}{5}}$
	$-48$

[/hidden-answer]

Try it

[ohm_question]156968[/ohm_question]

Watch the following video to see more examples of how to multiply a fraction and a whole number,

Thumbnail for the embedded element "Ex 2: Multiply Fractions"

A YouTube element has been excluded from this version of the text. You can view it online here: http://pb.libretexts.org/afm-2/?p=60

Reciprocals

The fractions $\frac{2}{3}$ and $\frac{3}{2}$ are related to each other in a special way. So are $-\frac{10}{7}$ and $-\frac{7}{10}$ . Do you see how? Besides looking like upside-down versions of one another, if we were to multiply these pairs of fractions, the product would be $1$ .

$\frac{2}{3}\cdot \frac{3}{2}=1\text{ and }-\frac{10}{7}\left(-\frac{7}{10}\right)=1$

Such pairs of numbers are called reciprocals.

Reciprocal

The reciprocal of the fraction $\frac{a}{b}$ is $\frac{b}{a}$ , where $a\ne 0$ and $b\ne 0$ . A number and its reciprocal have a product of $1$ .

$\frac{a}{b}\cdot \frac{b}{a}=1$

To find the reciprocal of a fraction, we invert the fraction. This means that we place the numerator in the denominator and the denominator in the numerator. To get a positive result when multiplying two numbers, the numbers must have the same sign. So reciprocals must have the same sign.

To find the reciprocal, keep the same sign and invert the fraction. The number zero does not have a reciprocal. Why? A number and its reciprocal multiply to $1$ . Is there any number $r$ so that $0\cdot r=1?$ No. So, the number $0$ does not have a reciprocal.

Example

Find the reciprocal of each number. Then check that the product of each number and its reciprocal is $1$ .

$\frac{4}{9}$
$-\frac{1}{6}$
$-\frac{14}{5}$
$7$

Solution:
To find the reciprocals, we keep the sign and invert the fractions.

1.
Find the reciprocal of $\frac{4}{9}$ .	The reciprocal of $\frac{4}{9}$ is $\frac{9}{4}$ .
Check:
Multiply the number and its reciprocal.	$\frac{4}{9}\cdot \frac{9}{4}$
Multiply numerators and denominators.	$\frac{36}{36}$
Simplify.	$1\quad\checkmark$

2.
Find the reciprocal of $-\frac{1}{6}$ .	$-\frac{6}{1}$
Simplify.	$-6$
Check:	$-\frac{1}{6}\cdot \left(-6\right)$
	$1\quad\checkmark$

3.
Find the reciprocal of $-\frac{14}{5}$ .	$-\frac{5}{14}$
Check:	$-\frac{14}{5}\cdot \left(-\frac{5}{14}\right)$
	$\frac{70}{70}$
	$1\quad\checkmark$

4.
Find the reciprocal of $7$ .
Write $7$ as a fraction.	$\frac{7}{1}$
Write the reciprocal of $\frac{7}{1}$ .	$\frac{1}{7}$
Check:	$7\cdot \left(\frac{1}{7}\right)$
	$1\quad\checkmark$

Try It

[ohm_question]141842[/ohm_question]

In the following video we will show more examples of how to find the reciprocal of integers, fractions and mixed numbers.

Thumbnail for the embedded element "Ex: Determine the Reciprocal of Integers, Fractions, and Mixed Numbers"

A YouTube element has been excluded from this version of the text. You can view it online here: http://pb.libretexts.org/afm-2/?p=60

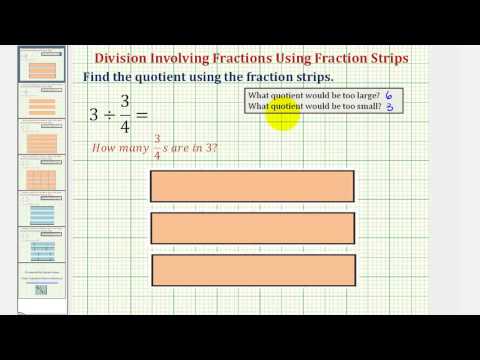
Dividing Fractions

Why is $12\div 3=4?$ We previously modeled this with counters. How many groups of $3$ counters can be made from a group of $12$ counters?

Four red ovals are shown. Inside each oval are three grey circles.
There are $4$ groups of $3$ counters. In other words, there are four $3\text{s}$ in $12$ . So, $12\div 3=4$ .

What about dividing fractions? Suppose we want to find the quotient: $\frac{1}{2}\div \frac{1}{6}$ . We need to figure out how many $\frac{1}{6}\text{s}$ there are in $\frac{1}{2}$ . We can use fraction tiles to model this division. We start by lining up the half and sixth fraction tiles as shown below. Notice, there are three $\frac{1}{6}$ tiles in $\frac{1}{2}$ , so $\frac{1}{2}\div \frac{1}{6}=3$ .

A rectangle is shown, labeled as one half. Below it is an identical rectangle split into three equal pieces, each labeled as one sixth.

Example

Model: $\frac{1}{4}\div \frac{1}{8}$

Solution:
We want to determine how many $\frac{1}{8}\text{s}$ are in $\frac{1}{4}$ . Start with one $\frac{1}{4}$ tile. Line up $\frac{1}{8}$ tiles underneath the $\frac{1}{4}$ tile.

A rectangle is shown, labeled one fourth. Below it is an identical rectangle split into two equal pieces, each labeled as one eighth.
There are two $\frac{1}{8}\text{s}$ in $\frac{1}{4}$ .
So, $\frac{1}{4}\div \frac{1}{8}=2$ .

The following video shows a whole number being divided by a fraction using a slightly different method.

Thumbnail for the embedded element "Ex: Find the Quotient of a Whole Number and Fraction using Fraction Strips"

A YouTube element has been excluded from this version of the text. You can view it online here: http://pb.libretexts.org/afm-2/?p=60

Example

Model: $2\div \frac{1}{4}$
[reveal-answer q=”391699″]Show Answer[/reveal-answer]
[hidden-answer a=”391699″]

Solution:
We are trying to determine how many $\frac{1}{4}\text{s}$ there are in $2$ . We can model this as shown.

Two rectangles are shown, each labeled as 1. Below it are two identical rectangle, each split into four pieces. Each of the eight pieces is labeled as one fourth.
Because there are eight $\frac{1}{4}\text{s}$ in $2,2\div \frac{1}{4}=8$ .

[/hidden-answer]

Try It

Model: $2\div \frac{1}{3}$
[reveal-answer q=”73567″]Show Answer[/reveal-answer]
[hidden-answer a=”73567″]

Two rectangles are shown, each labeled as 1. Below it are two identical rectangle, each split into three pieces. Each of the six pieces is labeled as one third.

[/hidden-answer]

Model: $3\div \frac{1}{2}$
[reveal-answer q=”354856″]Show Answer[/reveal-answer]
[hidden-answer a=”354856″]

Three rectangles are shown, each labeled as 1. Below are three identical rectangles, each split into 2 equal pieces. Each of these six pieces is labeled as one half.

[/hidden-answer]

[ohm_question height=”270″]117216[/ohm_question]

Let’s use money to model $2\div \frac{1}{4}$ in another way. We often read $\frac{1}{4}$ as a ‘quarter’, and we know that a quarter is one-fourth of a dollar as shown in the image below. So we can think of $2\div \frac{1}{4}$ as, “How many quarters are there in two dollars?” One dollar is $4$ quarters, so $2$ dollars would be $8$ quarters. So again, $2\div \frac{1}{4}=8$ .

Using fraction tiles, we showed that $\frac{1}{2}\div \frac{1}{6}=3$ . Notice that $\frac{1}{2}\cdot \frac{6}{1}=3$ also. How are $\frac{1}{6}$ and $\frac{6}{1}$ related? They are reciprocals. This leads us to the procedure for fraction division.

Fraction Division

If $a,b,c,\text{ and }d$ are numbers where $b\ne 0,c\ne 0,\text{ and }d\ne 0$ , then $\frac{a}{b}\div \frac{c}{d}=\frac{a}{b}\cdot \frac{d}{c}$

To divide fractions, multiply the first fraction by the reciprocal of the second.

We need to say $b\ne 0,c\ne 0\text{ and }d\ne 0$ to be sure we don’t divide by zero.

Example

Divide, and write the answer in simplified form: $\frac{2}{5}\div \left(-\frac{3}{7}\right)$
[reveal-answer q=”261121″]Show Answer[/reveal-answer]
[hidden-answer a=”261121″]

Solution:

$\frac{2}{5}\div \left(-\frac{3}{7}\right)$
Multiply the first fraction by the reciprocal of the second.	$\frac{2}{5}\left(-\frac{7}{3}\right)$
Multiply. The product is negative.	$-\frac{14}{15}$

[/hidden-answer]

Try It

[ohm_question height=”270″]146066[/ohm_question]

[ohm_question height=”270″]146067[/ohm_question]

Watch this video for more examples of dividing fractions using a reciprocal.

Thumbnail for the embedded element "Ex 2: Divide Fractions"

A YouTube element has been excluded from this version of the text. You can view it online here: http://pb.libretexts.org/afm-2/?p=60

Example

Divide, and write the answer in simplified form: $\frac{7}{18}\div \frac{14}{27}$
[reveal-answer q=”987562″]Show Answer[/reveal-answer]
[hidden-answer a=”987562″]

Solution:

	$\frac{7}{18}\div \frac{14}{27}$
Multiply the first fraction by the reciprocal of the second.	$\frac{7}{18}\cdot \frac{27}{14}$
Multiply.	$\frac{7\cdot 27}{18\cdot 14}$
Rewrite showing common factors.	$\frac{\color{red}{7}\cdot\color{blue}{9}\cdot3}{\color{blue}{9}\cdot2\cdot\color{red}{7}\cdot2}$
Remove common factors.	$\frac{3}{2\cdot 2}$
Simplify.	$\frac{3}{4}$