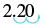1.8: Writing Fractions and Decimals as Percents
- Page ID
- 45767
Learning Outcome
- Use percent to represent a given fraction or decimal
How many cents are in one dollar? There are cents in a dollar. How many years are in a century? There are
years in a century. Does this give you a clue about what the word “percent” means? It is really two words, “per cent,” and means per one hundred. A percent is a ratio whose denominator is
. We use the percent symbol,
, to show percent.
Percent
A percent is a ratio whose denominator is .
For example
According to data from the American Association of Community Colleges , about
of community college students are female. This means
out of every
community college students are female, as the image below shows. Out of the
squares on the grid,
are shaded, which we write as the ratio
.
Among every community college students,
are female.

Similarly, means a ratio of
means a ratio of
and
means a ratio of
. In words, “one hundred percent” means the total
is
, and since
, we see that
means
whole.
To convert a decimal to a percent, remember that percent means per hundred. If we change the decimal to a fraction whose denominator is , it is easy to change that fraction to a percent.
Convert a decimal to a percent
- Write the decimal as a fraction.
- If the denominator of the fraction is not
, rewrite it as an equivalent fraction with denominator
.
- Write this ratio as a percent.
example
Convert each decimal to a percent:
1.
2.
Solution
| 1. | |
| Write as a fraction. Five hundredths – the denominator is | |
| Write this ratio as a percent. |
| 2. | |
| Write as a fraction. Eighty-three hundredths – the denominator is | |
| Write this ratio as a percent. |
try it
[ohm_question]146666[/ohm_question]
Let’s look at a few more examples of converting decimals to percents, but these aren’t as straight forward!
example
Convert each decimal to a percent:
1.
2.
2.
[reveal-answer q=”740440″]Show Answer[/reveal-answer]
[hidden-answer a=”740440″]
Solution
| 1. | |
| Write as a fraction. The denominator is | |
| Multiply the numerator and denominator by | |
| Write this ratio as a percent. |
Notice that you could also have written as
and gotten to
without doing any calculations.
| 2. | |
| Write as a fraction. | |
| Write as an improper fraction. The denominator is | |
| Write this ratio as a percent. |
Notice that since , the result is more than
| 3. | |
| Write as a fraction. The denominator is | |
| Divide the numerator and denominator by | |
| Write this ratio as a percent. |
Notice that any decimal that has value beyond the hundredths place will have a decimal answer when converted to a percent.
[/hidden-answer]
try it
[ohm_question]146667[/ohm_question]
[ohm_question]156959[/ohm_question]
[ohm_question]156964[/ohm_question]
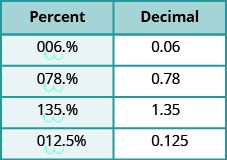
Let’s summarize some of the results from the previous examples in the table below so we can look for a pattern.
| Decimal | Percent |
|---|---|
Do you see the pattern? To convert a decimal to a percent, we move the decimal point two places to the right and then add the percent sign.
The next table uses the decimal numbers in the table above and shows visually to convert them to percents by moving the decimal point two places to the right and then writing the sign.
In an earlier lesson, we learned how to convert fractions to decimals. Now we also know how to change decimals to percents. So to convert a fraction to a percent, we first change it to a decimal and then convert that decimal to a percent.
Convert a fraction to a percent
- If possible, convert the fraction to a denominator of
.
- If not, convert the fraction to a decimal by dividing.
- Convert the decimal to a percent.
example
Convert each fraction or mixed number to a percent:
1.
2.
3.
[reveal-answer q=”32099″]Show Answer[/reveal-answer]
[hidden-answer a=”32099″]
Solution
To convert a fraction to a decimal, divide the numerator by the denominator.
| 1. | |
| Change to a decimal. | 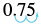 |
| Write as a percent by moving the decimal two places. |
| 2. | |
| Change to a decimal. | 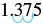 |
| Write as a percent by moving the decimal two places. |
| 3. | |
| Write as an improper fraction. | |
| Change to a decimal. |
|
| Write as a percent. |
Notice that we sometimes need to add zeros at the end of the number when moving the decimal two places to the right.
[/hidden-answer]
Sometimes when changing a fraction to a decimal, the division continues for many decimal places and we will need to round off the quotient. Typically, you will round before converting to a percent unless instructed otherwise. The number of decimal places we round to will depend on the situation. If the decimal calculation involves money, we round it to the hundredths place. For most other cases, we will round the number to the nearest thousandth, so the percent will be rounded to the nearest tenth.
try it
[ohm_question]146669[/ohm_question]
[ohm_question]146670[/ohm_question]
[ohm_question]146671[/ohm_question]
- Prealgebra. Provided by: OpenStax. License: CC BY: Attribution. License Terms: Download for free at http://cnx.org/contents/caa57dab-41c...cda5519c@9.757