3.3: Equivalent Units (Weighted Average)
- Page ID
- 26045
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Essentially, the concept of equivalent units involves expressing a given number of partially completed units as a smaller number of fully completed units. We do this because it is easier to account for whole units then parts of a unit. We are adding together partially completed units to make a whole unit. For example, if we have 3 units 1/3 of the way complete, we can add them together to make 1 equivalent unit (1/3 + 1/3 + 1/3). We can make this calculation easier by multiplying the units by a percentage of complete.
For example, if we bring 1,000 units to a 40 % state of completion, this is equivalent to 400 units (1,000 x 40%) that are 100% complete. Accountants base this concept on the supposition that a company must incur approximately the same amount of costs to bring 1,000 units to a 40% level of completion as it would to complete 400 units.
Here is a diagram of the concept of equivalent units. As you examine the diagram, think of the amount of water in the glasses as costs that the company has already incurred.
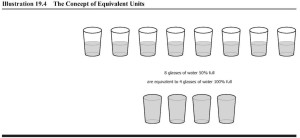
Now, watch the video for another example.
| Units in Beg. Work in Process | Units Completed and Transferred |
| + Units Started this period | + Units in End. Work in Process |
| = Total Units | = Total Units |
The total units in each column must agree with one another. This formula explains how many units we had to work with (including units in beginning work in process + units started this period) and what happened to those units (units completed or units remain in work in process inventory since there are not complete).
Under the weighted average method, equivalent units are calculated based on 2 things: units completed and transferred out and units in ending work in process inventory.
Units completed and transferred are finished units and will always be 100% complete for equivalent unit calculations for direct materials, direct labor and overhead. For units in ending work in process, we would take the units unfinished x a percent complete. The percent complete can be different for direct materials, direct labor or overhead.
Example – Jax Company
Assume that Jax Company manufactures and sells a chemical product used to clean kitchen counters and sinks. The company processes the product in two departments. Department A crushes powders and blends the basic materials. Department B packages the product and transfers it to finished goods. We will look at equivalent units for Department B. The June production data for Department B is:
| Department B | |
| Beginning work in process | -0- |
| Units started this period | 11,000 |
| Units completed and transferred | 9,000 |
| Ending work in process units | 2,000 |
| Direct materials | $ 1,100 |
| Direct labor | $ 2,880 |
| Applied overhead | $ 8,880 |
The physical flow of units shows:
| Units in Beg. WIP | -0- | Units Completed and Transferred | 9,000 | |
| Units Started this period | 11,000 | Units in End. WIP | 2,000 | |
| Total Units | 11,000 | = | Total Units | 11,000 |
The beginning step in computing Department B’s equivalent units for Jax Company is determining the stage of completion of the 2,000 unfinished units (remember units completed and transferred are always 100% complete). In Department B, the ending units may be in different stages of completion regarding the materials, labor, and overhead costs. Assume that Department B adds all materials at the beginning of the production process. Then ending inventory would be 100% complete as to materials since we received all materials at the beginning of the process.
Accountants often assume that units are at the same stage of completion for both labor and overhead. Accountants call the combined labor and overhead costs conversion costs. Conversion costs are those costs incurred to convert raw materials into the final product (meaning, direct labor and overhead).
Let us assume that, on average, the 2,000 units in ending inventory are 40% complete as to conversion costs. This means that Department B transferred out 9,000 units fully completed and brought 2,000 units to a 40% completion state. Department B now has an equivalent of 800 fully completed units remaining in inventory (800 = 2,000 X 40 per cent).
The equivalent units for materials, labor and overhead would be calculated as:
| Materials | Conversion Costs | |
| Units Completed and Transferred | 9,000 | 9,000 |
| (9,000 x 100% complete) | ||
| Units in Ending WIP | ||
| Materials (2,000 x 100% complete) | 2,000 | |
| Conversion Cost (2,000 x 40% complete) | 800 | |
| Total Equivalent Units | 11,000 | 9,800 |
Total equivalent units for each cost element (materials, conversion cost) is calculated as:
Equivalent units = Units completed + (Units in ending inventory X percent complete)
The key to equivalent units is determining the percent complete, especially for materials can be confusing. Common terms you will see when determine ending work in process percent complete:
| Description | % Complete |
| Materials added at the beginning of the process | 100% complete for materials |
| Materials added evenly through out the process | Use % complete for ending WIP |
| Materials added at the end of the process | 0% complete for materials |
- Accounting Principles: A Business Perspective.. Authored by: James Don Edwards, University of Georgia & Roger H. Hermanson, Georgia State University.. Provided by: Endeavour International Corporation. Project: The Global Text Project.. License: CC BY: Attribution
- 20-- The Concept of Equivalent Units of Production. Authored by: Larry Walther. Located at: youtu.be/IMhBXeb0IsY. License: All Rights Reserved. License Terms: Standard YouTube License


