6.E: Exercises (Part 1)
- Page ID
- 1767
Questions
- Describe the components of the profit equation.
- What is the difference between a variable cost and a fixed cost? Provide examples of each.
- You are asked to find the break-even point in units and in sales dollars. What does this mean?
- You are asked to find the target profit in units and in sales dollars. What does this mean?
- For a company with one product, describe the equation used to calculate the break-even point or target profit in (a) units, and (b) sales dollars.
- Distinguish between contribution margin per unit and contribution margin ratio.
- What does the term margin of safety mean? How might management use this information?
- Review Note 6.16 "Business in Action 6.1" How do airlines measure break-even points? In 2001, which airline had the lowest break-even point?
- How does the break-even point equation change for a company with multiple products or services compared to a single-product company?
- Describe the assumptions made to simplify the cost-volume-profit analysis described in the chapter.
- What is sensitivity analysis and how might it help those performing cost-volume-profit analysis?
- Review Note 6.37 "Business in Action 6.2" What were the owners concerned about with regards to projected profits? What were the results of the calculations made to address the owners’ concerns?
- If you are asked to review the cost structure of an organization, what are you being asked to do?
- When might the contribution margin per unit of constraint be more effective than the contribution margin per unit for making decisions?
- Describe the three steps used to calculate the target profit for companies that incur income tax costs.
- Describe the difference between absorption costing and variable costing.
- Why do some organizations use variable costing?
Brief Exercises
- Planning at Snowboard Company. Refer to the dialogue at Snowboard Company presented at the beginning of the chapter. What information is Recilia, vice president of sales, requesting from Lisa, the company accountant? How does Recilia plan on using this information?
- Contribution Margin Calculations. Ace Company sells lawn mowers for $200 per unit. Variable cost per unit is $40, and fixed costs total $4,000. Find (a) the contribution margin per unit, and (b) the contribution margin ratio.
- Weighted Average Contribution Margin Calculation. Radio Control, Inc., sells radio controlled cars for $300 per unit representing 80 percent of total sales, and radio controlled boats for $400 per unit representing 20 percent of total sales. Variable cost per unit is $150 for cars and $300 for boats. Find (a) the contribution margin per unit for each product, and (b) the weighted average contribution margin per unit.
- Sensitivity Analysis, Sales Price. Refer to the base case for Snowboard Company presented in the first column of Figure 6.6. Assume the unit sales price decreases by 10 percent. Calculate (a) the new projected profit, (b) the dollar change in profit from the base case, and (c) the percent change in profit from the base case.
- Sensitivity Analysis, Unit Sales. Refer to the base case for Snowboard Company presented in the first column of Figure 6.6. Assume the number of units sold increases by 10 percent. Calculate (a) the new projected profit, (b) the dollar change in profit from the base case, and (c) the percent change in profit from the base case.
- Operating Leverage. High operating leverage means:
- The company has relatively low fixed costs.
- The company has relatively high fixed costs.
- The company will have to sell more units than a comparable company with low operating leverage to break even.
- The company will have to sell fewer units than a comparable company with low operating leverage to break even.
- Both (2) and (3) are correct.
- Both (1) and (4) are correct.
- Contribution Margin per Unit of Constraint. Paint Toys Company sells paint ball guns for $100 per unit. Variable cost is $60 per unit. Each paint ball gun requires 1.25 machine hours and 2.00 direct labor hours to produce. Calculate the contribution margin (a) per unit, (b) per machine hour, and (c) per direct labor hour.
- Target Profit with Taxes. Management of Lakewood Company would like to achieve a target profit after taxes of $300,000. The company’s income tax rate is 40 percent. What target profit before taxes is required to achieve the $300,000 after-tax profit desired by management?
- Absorption Costing Versus Variable Costing. Describe the difference between absorption costing and variable costing. Which approach yields the highest profit when the units produced are greater than the units sold? Explain.
Exercises: Set A
- Break-Even Point and Target Profit Measured in Units (Single Product). Nellie Company has monthly fixed costs totaling $100,000 and variable costs of $20 per unit. Each unit of product is sold for $25.
Required:
- Calculate the contribution margin per unit.
- Find the break-even point in units.
- How many units must be sold to earn a monthly profit of $40,000?
- Break-Even Point and Target Profit Measured in Sales Dollars (Single Product). Nellie Company has monthly fixed costs totaling $100,000 and variable costs of $20 per unit. Each unit of product is sold for $25 (these data are the same as the previous exercise):
Required:
- Calculate the contribution margin ratio.
- Find the break-even point in sales dollars.
- What amount of sales dollars is required to earn a monthly profit of $60,000?
- Margin of Safety (Single Product). Nellie Company has monthly fixed costs totaling $100,000 and variable costs of $20 per unit. Each unit of product is sold for $25 (these data are the same as the previous exercise). Assume Nellie Company expects to sell 24,000 units of product this coming month.
Required:
- Find the margin of safety in units.
- Find the margin of safety in sales dollars.
- Break-Even Point and Target Profit Measured in Units (Multiple Products). Hi-Tech Incorporated produces two different products with the following monthly data.
| Cell | GPS | Total | |
|---|---|---|---|
| Selling price per unit | $100 | $400 | |
| Variable cost per unit | $40 | $240 | |
| Expected unit sales | 21,000 | 9,000 | 30,000 |
| Sales mix | 70 percent | 30 percent | 100 percent |
| Fixed costs | $1,800,000 |
Assume the sales mix remains the same at all levels of sales.
Required:
- Calculate the weighted average contribution margin per unit.
- How many units in total must be sold to break even?
- How many units of each product must be sold to break even?
- How many units in total must be sold to earn a monthly profit of $180,000?
- How many units of each product must be sold to earn a monthly profit of $180,000?
- Break-Even Point and Target Profit Measured in Sales Dollars (Multiple Products). Hi-Tech Incorporated produces two different products with the following monthly data (these data are the same as the previous exercise).
| Cell | GPS | Total | |
|---|---|---|---|
| Selling price per unit | $100 | $400 | |
| Variable cost per unit | $40 | $240 | |
| Expected unit sales | 21,000 | 9,000 | 30,000 |
| Sales mix | 70 percent | 30 percent | 100 percent |
| Fixed costs | $1,800,000 |
Assume the sales mix remains the same at all levels of sales.
Required:
Round your answers to the nearest hundredth of a percent and nearest dollar where appropriate. (An example for percentage calculations is 0.434532 = 0.4345 = 43.45 percent; an example for dollar calculations is $378.9787 = $379.)
- Using the information provided, prepare a contribution margin income statement for the month similar to the one in Figure 6.5.
- Calculate the weighted average contribution margin ratio.
- Find the break-even point in sales dollars.
- What amount of sales dollars is required to earn a monthly profit of $540,000?
- Assume the contribution margin income statement prepared in requirement a is the company’s base case. What is the margin of safety in sales dollars?
- Changes in Sales Mix. Hi-Tech Incorporated produces two different products with the following monthly data (these data are the same as the previous exercise).
| Cell | GPS | Total | |
|---|---|---|---|
| Selling price per unit | $100 | $400 | |
| Variable cost per unit | $40 | $240 | |
| Expected unit sales | 21,000 | 9,000 | 30,000 |
| Sales mix | 70 percent | 30 percent | 100 percent |
| Fixed costs | $1,800,000 |
Required:
- If the sales mix shifts to 50 percent Cell and 50 percent GPS, would the break-even point in units increase or decrease? Explain. (Detailed calculations are not necessary but may be helpful in confirming your answer.)
- Go back to the original projected sales mix. If the sales mix shifts to 80 percent Cell and 20 percent GPS, would the break-even point in units increase or decrease? Explain. (Detailed calculations are not necessary but may be helpful in confirming your answer.)
- CVP Sensitivity Analysis (Single Product). Bridgeport Company has monthly fixed costs totaling $200,000 and variable costs of $40 per unit. Each unit of product is sold for $50. Bridgeport expects to sell 30,000 units each month (this is the base case).
Required:
For each of the independent situations in requirements b through d, assume that the number of units sold remains at 30,000.
- Prepare a contribution margin income statement for the base case.
- Refer to the base case. What would the operating profit be if the unit sales price increases 10 percent?
- Refer to the base case. What would the operating profit be if the unit variable cost decreases 20 percent?
- Refer to the base case. What would the operating profit be if total fixed costs decrease 20 percent?
- CVP Sensitivity Analysis (Multiple Products). Gonzalez Company produces two different products that have the following monthly data (this is the base case).
| Cruiser | Racer | Total | |
|---|---|---|---|
| Selling price per unit | $300 | $1,200 | |
| Variable cost per unit | $120 | $720 | |
| Expected unit sales | 1,400 | 600 | 2,000 |
| Sales mix | 70 percent | 30 percent | 100 percent |
| Fixed costs | $180,000 |
Required:
For each of the independent situations in requirements b through d, assume that total sales remains at 2,000 units.
- Prepare a contribution margin income statement.
- Refer to the base case. What would the operating profit be if the Cruiser sales price (1) increases 20 percent, or (2) decreases 20 percent?
- Refer to the base case. What would the operating profit be if the Cruiser sales volume increases 400 units with a corresponding decrease of 400 units in Racer sales?
- Refer to the base case. What would the operating profit be if total fixed costs increase five percent? Does this increase in fixed costs result in higher operating leverage or lower operating leverage? Explain.
- Contribution Margin with Resource Constraints. CyclePath Company produces two different products that have the following price and cost characteristics.
| Bicycle | Tricycle | |
|---|---|---|
| Selling price per unit | $200 | $100 |
| Variable cost per unit | $120 | $50 |
Management believes that pushing sales of the Bicycle product would maximize company profits because of the high contribution margin per unit for this product. However, only 50,000 labor hours are available each year, and the Bicycle product requires 4 labor hours per unit while the Tricycle model requires 2 labor hours per unit. The company sells everything it produces.
Required:
- Calculate the contribution margin per unit of constrained resource for each model.
- Which model would CyclePath prefer to sell to maximize overall company profit? Explain.
- Target Profit Measured in Units (with Taxes). Optical Incorporated has annual fixed costs totaling $6,000,000 and variable costs of $350 per unit. Each unit of product is sold for $500. Assume a tax rate of 20 percent.
Required:
Use the three steps described in the chapter to determine how many units must be sold to earn an annual profit of $100,000 after taxes. (Round to the nearest unit.)
- Target Profit Measured in Sales Dollars (with Taxes). Optical Incorporated has annual fixed costs totaling $6,000,000 and variable costs of $350 per unit. Each unit of product is sold for $500. Assume a tax rate of 20 percent (these data are the same as the previous exercise).
Required:
Use the three steps described in the chapter to determine the sales dollars required to earn an annual profit of $150,000 after taxes.
- Absorption Costing Versus Variable Costing. Technic Company produces portable CD players. The company has no finished goods inventory at the beginning of year 1. The following information pertains to Technic Company.
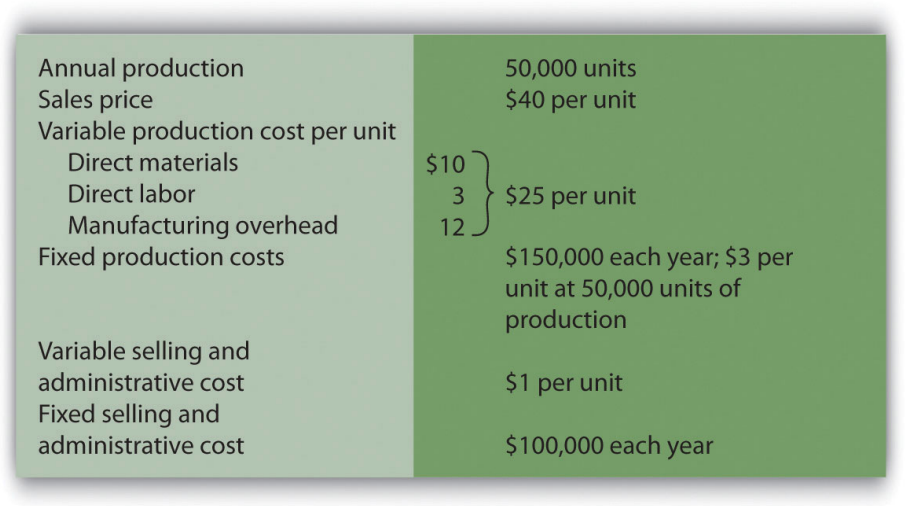
Required:
- All 50,000 units produced during year 1 are sold during year 1.
- Prepare a traditional income statement assuming the company uses absorption costing.
- Prepare a contribution margin income statement assuming the company uses variable costing.
- Although 50,000 units are produced during year 2, only 40,000 are sold during the year. The remaining 10,000 units are in finished goods inventory at the end of year 2.
- Prepare a traditional income statement assuming the company uses absorption costing.
- Prepare a contribution margin income statement assuming the company uses variable costing.
Exercises: Set B
- Break-Even Point and Target Profit Measured in Units (Single Product). Phan Incorporated has annual fixed costs totaling $6,000,000 and variable costs of $350 per unit. Each unit of product is sold for $500.
Required:
- Calculate the contribution margin per unit.
- Find the break-even point in units.
- How many units must be sold to earn an annual profit of $750,000?
- Break-Even Point and Target Profit Measured in Sales Dollars (Single Product). Phan Incorporated has annual fixed costs totaling $6,000,000 and variable costs of $350 per unit. Each unit of product is sold for $500 (these data are the same as the previous exercise).
Required:
- Calculate the contribution margin ratio.
- Find the break-even point in sales dollars.
- What amount of sales dollars is required to earn an annual profit of $300,000?
- Margin of Safety (Single Product). Phan Incorporated has annual fixed costs totaling $6,000,000 and variable costs of $350 per unit. Each unit of product is sold for $500 (these data are the same as the previous exercise). Assume Phan Incorporated expects to sell 51,000 units of product this coming year.
Required:
- Find the margin of safety in units.
- Find the margin of safety in sales dollars.
- Break-Even Point and Target Profit Measured in Units (Multiple Products). Advanced Products Company produces three different CDs with the following annual data.
| Music | Data | DVD | Total | |
|---|---|---|---|---|
| Selling price per unit | $10 | $4 | $12 | |
| Variable cost per unit | $3 | $1 | $3 | |
| Expected unit sales | 8,000 | 10,000 | 22,000 | 40,000 |
| Sales mix | 20 percent | 25 percent | 55 percent | 100 percent |
| Fixed costs | $205,900 |
Assume the sales mix remains the same at all levels of sales.
Required:
(Round all answers to the nearest cent and nearest unit where appropriate.)
- Calculate the weighted average contribution margin per unit.
- How many units in total must be sold to break even?
- How many units of each product must be sold to break even?
- How many units in total must be sold to earn an annual profit of $200,000?
- How many units of each product must be sold to earn an annual profit of $200,000?
- Break-Even Point and Target Profit Measured in Sales Dollars (Multiple Products). Advanced Products Company produces three different CDs with the following annual data (these data are the same as the previous exercise).
| Music | Data | DVD | Total | |
|---|---|---|---|---|
| Selling price per unit | $10 | $4 | $12 | |
| Variable cost per unit | $3 | $1 | $3 | |
| Expected unit sales | 8,000 | 10,000 | 22,000 | 40,000 |
| Sales mix | 20 percent | 25 percent | 55 percent | 100 percent |
| Fixed costs | $205,900 |
Assume the sales mix remains the same at all levels of sales.
Required:
Round your answers to the nearest hundredth of a percent and nearest dollar where appropriate. (An example for percentage calculations is 0.434532 = 0.4345 = 43.45 percent; an example for dollar calculations is $378.9787 = $379.)
- Using the information provided, prepare a contribution margin income statement similar to the one in Figure 6.5.
- Calculate the weighted average contribution margin ratio.
- Find the break-even point in sales dollars.
- What amount of sales dollars is required to earn an annual profit of $200,000?
- Assume the contribution margin income statement prepared in requirement a is the company’s base case. What is the margin of safety in sales dollars?
- Changes in Sales Mix. Advanced Products Company produces three different CDs with the following annual data (these data are the same as the previous exercise).
| Music | Data | DVD | Total | |
|---|---|---|---|---|
| Selling price per unit | $10 | $4 | $12 | |
| Variable cost per unit | $3 | $1 | $3 | |
| Expected unit sales | 8,000 | 10,000 | 22,000 | 40,000 |
| Sales mix | 20 percent | 25 percent | 55 percent | 100 percent |
| Fixed costs | $205,900 |
Required:
If the sales mix shifts more toward the Data product than the other two products, would the break-even point in units increase or decrease? Explain. (Detail calculations are not necessary, but may be helpful in confirming your answer.)
- CVP Sensitivity Analysis (Single Product). Skyler Incorporated has monthly fixed costs of $1,000,000 and variable costs of $24 per unit. Each unit of product is sold for $120. Skyler expects to sell 15,000 units each month (this is the base case).
Required:
For each of the independent situations in requirements b through d, assume that the number of units sold remains at 15,000. (Round to the nearest cent where appropriate.)
- Prepare a contribution margin income statement for the base case.
- Refer to the base case. What would the operating profit be if the unit sales price decreases 10 percent?
- Refer to the base case. What would the operating profit be if the unit variable cost increases 10 percent?
- Refer to the base case. What would the operating profit be if total fixed costs decrease 20 percent?
- CVP Sensitivity Analysis (Multiple Products). CyclePath Company produces two different products that have the following annual data (this is the base case).
| Music | Data | Total | |
|---|---|---|---|
| Selling price per unit | $200 | $100 | |
| Variable cost per unit | $120 | $50 | |
| Expected unit sales | 5,000 | 20,000 | 25,000 |
| Sales mix | 20 percent | 80 percent | 100 percent |
| Fixed costs | $1,000,000 |
Required:
For each of the independent situations in requirements b through d, assume that total sales remains at 25,000 units.
- Prepare a contribution margin income statement for the base case.
- Refer to the base case. What would the operating profit be if the Tricycle sales price (1) increases 10 percent, or (2) decreases 10 percent?
- Refer to the base case. What would the operating profit be if Bicycle sales volume decreases 500 units and there is a corresponding increase of 500 units in Tricycle sales?
- Refer to the base case. What would the operating profit be if total fixed costs decrease 10 percent? Does this decrease in fixed costs result in higher operating leverage or lower operating leverage? Explain.
- Contribution Margin with Resource Constraints. CyclePath Company produces two different products that have the following price and cost characteristics.
| Bicycle | Tricycle | |
|---|---|---|
| Selling price per unit | $200 | $100 |
| Variable cost per unit | $120 | $50 |
Management believes that pushing sales of the Bicycle product would maximize company profits because of the high contribution margin per unit for this product. However, only 23,000 machine hours are available each year, and the Bicycle product requires 2 machine hours per unit while the Tricycle model requires 1 machine hour per unit. The company sells everything it produces.
Required:
- Calculate the contribution margin per unit of constrained resource for each model.
- Which model would CyclePath prefer to sell to maximize overall company profit? Explain.
- Target Profit Measured in Units (with Taxes). Martis Company has annual fixed costs totaling $4,000,000 and variable costs of $300 per unit. Each unit of product is sold for $400. Assume a tax rate of 20 percent.
Required:
Use the three steps described in the chapter to determine how many units must be sold to earn an annual profit of $500,000 after taxes. (Round to the nearest unit.)
- Target Profit Measured in Sales Dollars (with Taxes). Martis Company has annual fixed costs totaling $4,000,000 and variable costs of $300 per unit. Each unit of product is sold for $400. Assume a tax rate of 20 percent (these data are the same as the previous exercise).
Required:
Use the three steps described in the chapter to determine the sales dollars required to earn an annual profit of $1,000,000 after taxes.
- Absorption Costing Versus Variable Costing. Photo Company produces digital cameras. The company has no finished goods inventory at the beginning of year 1. The following information pertains to Photo Company.
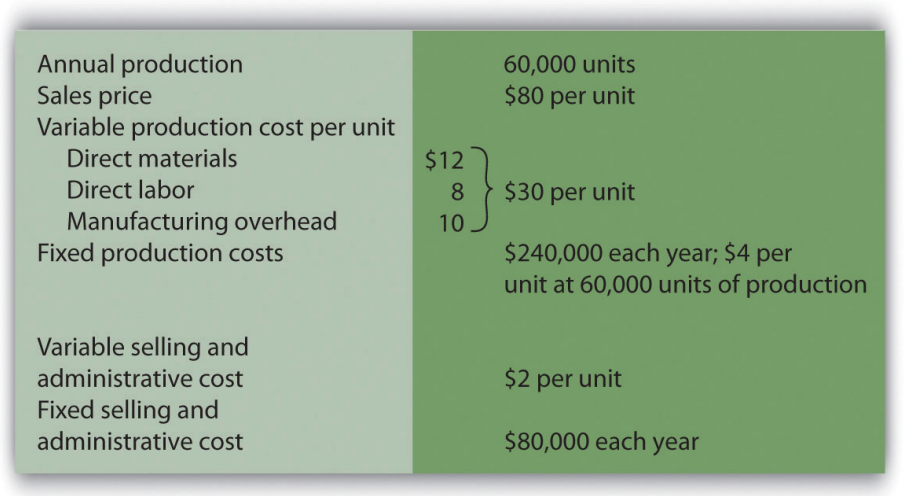
Required:
- All 60,000 units produced during year 1 are sold during year 1.
- Prepare a traditional income statement assuming the company uses absorption costing.
- Prepare a contribution margin income statement assuming the company uses variable costing.
- Although 60,000 units are produced during year 2, only 40,000 are sold during the year. The remaining 20,000 units are in finished goods inventory at the end of year 2.
- Prepare a traditional income statement assuming the company uses absorption costing.
- Prepare a contribution margin income statement assuming the company uses variable costing.


