3.2: Calculate a Break-Even Point in Units and Dollars
- Page ID
- 5194
In Building Blocks of Managerial Accounting, you learned how to determine and recognize the fixed and variable components of costs, and now you have learned about contribution margin. Those concepts can be used together to conduct cost-volume-profit (CVP) analysis, which is a method used by companies to determine what will occur financially if selling prices change, costs (either fixed or variable) change, or sales/production volume changes.
It is important, first, to make several assumptions about operations in order to understand CVP analysis and the associated contribution margin income statement. However, while the following assumptions are typical in CVP analysis, there can be exceptions. For example, while we typically assume that the sales price will remain the same, there might be exceptions where a quantity discount might be allowed. Our CVP analysis will be based on these assumptions:
- Costs are linear and can clearly be designated as either fixed or variable. In other words, fixed costs remain fixed in total over the relevant range and variable costs remain fixed on a per-unit basis. For example, if a company has the capability of producing up to \(1,000\) units a month of a product given its current resources, the relevant range would be \(0\) to \(1,000\). If they decided that they wanted to produce \(1,800\) units a month, they would have to secure additional production capacity. While they might be able to add an extra production shift and then produce \(1,800\) units a month without buying an additional machine that would increase production capacity to \(2,000\) units a month, companies often have to buy additional production equipment to increase their relevant range. In this example, the production capacity between \(1,800\) and \(2,000\) would be an expense that currently would not provide additional contribution toward fixed costs.
- Selling price per unit remains constant and does not increase or decrease based on volume (i.e., customers are not given discounts based on quantity purchased).
- In the case of manufacturing businesses, inventory does not change because we make the assumption that all units produced are sold.
- In the case of a company that sells multiple products, the sales mix remains constant. For example, if we are a beverage supplier, we might assume that our beverage sales are \(3\) units of coffee pods and two units of tea bags.
Using these assumptions, we can begin our discussion of CVP analysis with the break-even point.
Basics of the Break-Even Point
The break-even point is the dollar amount (total sales dollars) or production level (total units produced) at which the company has recovered all variable and fixed costs. In other words, no profit or loss occurs at break-even because Total Cost = Total Revenue. Figure \(\PageIndex{1}\) illustrates the components of the break-even point:
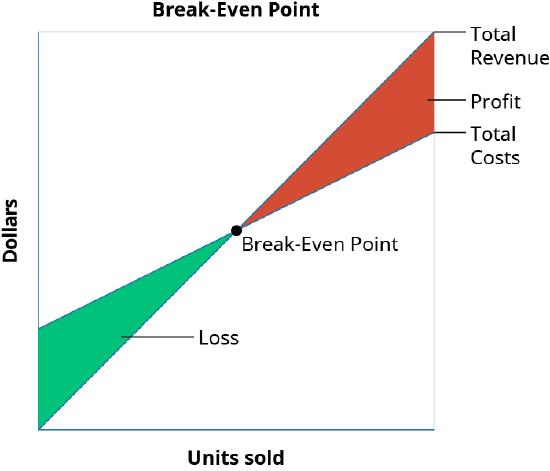
The basic theory illustrated in Figure \(\PageIndex{1}\) is that, because of the existence of fixed costs in most production processes, in the first stages of production and subsequent sale of the products, the company will realize a loss. For example, assume that in an extreme case the company has fixed costs of \(\$20,000\), a sales price of \(\$400\) per unit and variable costs of \(\$250\) per unit, and it sells no units. It would realize a loss of \(\$20,000\) (the fixed costs) since it recognized no revenue or variable costs. This loss explains why the company’s cost graph recognized costs (in this example, \(\$20,000\)) even though there were no sales. If it subsequently sells units, the loss would be reduced by \(\$150\) (the contribution margin) for each unit sold. This relationship will be continued until we reach the break-even point, where total revenue equals total costs. Once we reach the break-even point for each unit sold the company will realize an increase in profits of \(\$150\).
For each additional unit sold, the loss typically is lessened until it reaches the break-even point. At this stage, the company is theoretically realizing neither a profit nor a loss. After the next sale beyond the break-even point, the company will begin to make a profit, and the profit will continue to increase as more units are sold. While there are exceptions and complications that could be incorporated, these are the general guidelines for break-even analysis.
As you can imagine, the concept of the break-even point applies to every business endeavor—manufacturing, retail, and service. Because of its universal applicability, it is a critical concept to managers, business owners, and accountants. When a company first starts out, it is important for the owners to know when their sales will be sufficient to cover all of their fixed costs and begin to generate a profit for the business. Larger companies may look at the break-even point when investing in new machinery, plants, or equipment in order to predict how long it will take for their sales volume to cover new or additional fixed costs. Since the break-even point represents that point where the company is neither losing nor making money, managers need to make decisions that will help the company reach and exceed this point as quickly as possible. No business can operate for very long below break-even. Eventually the company will suffer losses so great that they are forced to close their doors.
The first step in determining the viability of the business decision to sell a product or provide a service is analyzing the true cost of the product or service and the timeline of payment for the product or service. Ethical managers need an estimate of a product or service's cost and related revenue streams to evaluate the chance of reaching the break-even point.
Determining an accurate price for a product or service requires a detailed analysis of both the cost and how the cost changes as the volume increases. This analysis includes the timing of both costs and receipts for payment, as well as how these costs will be financed. An example is an IT service contract for a corporation where the costs will be frontloaded. When costs or activities are frontloaded, a greater proportion of the costs or activities occur in an earlier stage of the project. An IT service contract is typically employee cost intensive and requires an estimate of at least \(120\) days of employee costs before a payment will be received for the costs incurred. An IT service contract for \(\$100,000\) in monthly services with a \(30\%\) profit margin will require \(4\) months of upfront financing of \(\$280,000\) balanced over the four months before a single payment is received.
The overall profit at a specific point in time requires a careful determination of all of the costs associated with creating and selling the product or providing the service. An ethical managerial accountant will provide a realistic cost estimate, regardless of management's desire to sell a product or provide a service. What might be a lucrative product on its face needs additional analysis provided by the managerial accountant.
To illustrate the concept of break-even, we will return to Hicks Manufacturing and look at the Blue Jay birdbath they manufacture and sell.
Watch this video of an example of performing the first steps of cost-volume-profit analysis to learn more.
Sales Where Operating Income Is \(\$0\)
Hicks Manufacturing is interested in finding out the point at which they break even selling their Blue Jay Model birdbath. They will break even when the operating income is \(\$0\). The operating income is determined by subtracting the total variable and fixed costs from the sales revenue generated by an enterprise. In other words, the managers at Hicks want to know how many Blue Jay birdbaths they will need to sell in order to cover their fixed expenses and break even. Information on this product is:

In order to find their break-even point, we will use the contribution margin for the Blue Jay and determine how many contribution margins we need in order to cover the fixed expenses, as shown below.
\[\text { Break-Even Point in Units: } \dfrac{\text { Total Fixed Costs }}{\text { Contribution Margin per Unit }}\]
Applying this to Hicks calculates as:
\[\dfrac{$18,000}{$80}=225\ \text { units} \nonumber\]
What this tells us is that Hicks must sell \(225\) Blue Jay Model birdbaths in order to cover their fixed expenses. In other words, they will not begin to show a profit until they sell the \(226^{th}\) unit. This is illustrated in their contribution margin income statement.

The break-even point for Hicks Manufacturing at a sales volume of \(\$22,500\) (\(225\) units) is shown graphically in Figure \(\PageIndex{4}\).
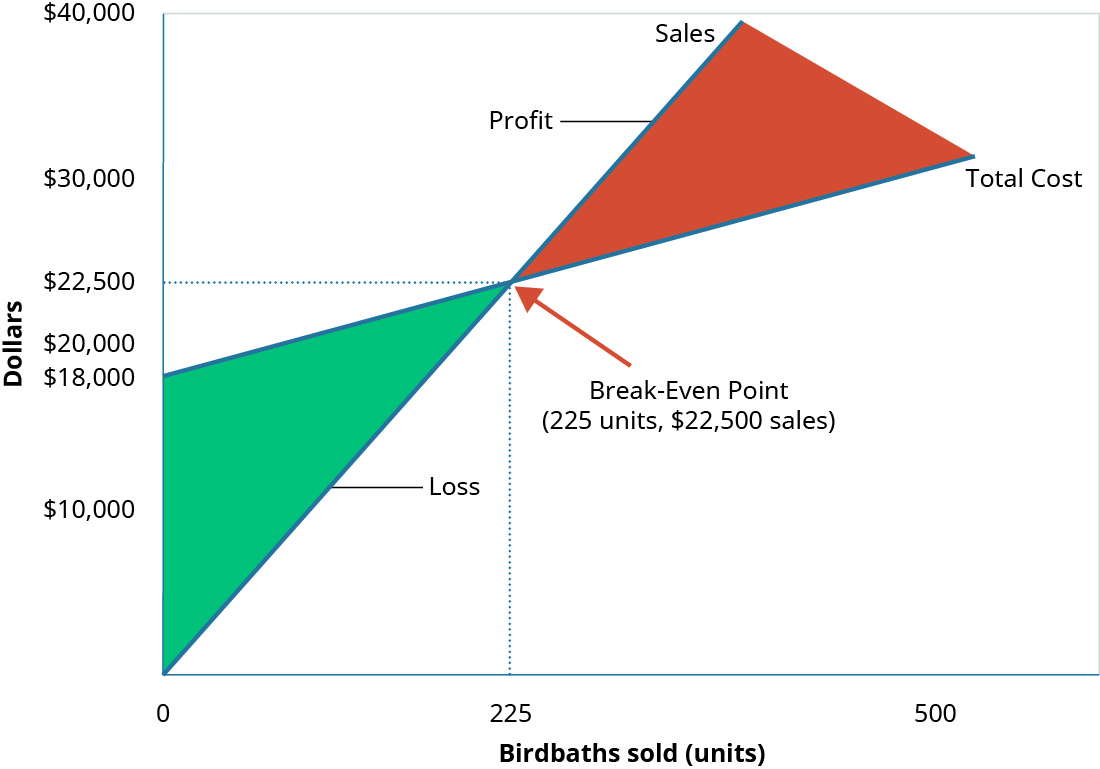
As you can see, when Hicks sells \(225\) Blue Jay Model birdbaths, they will make no profit, but will not suffer a loss because all of their fixed expenses are covered. However, what happens when they do not sell \(225\) units? If that happens, their operating income is negative.
Sales Where Operating Income Is Negative
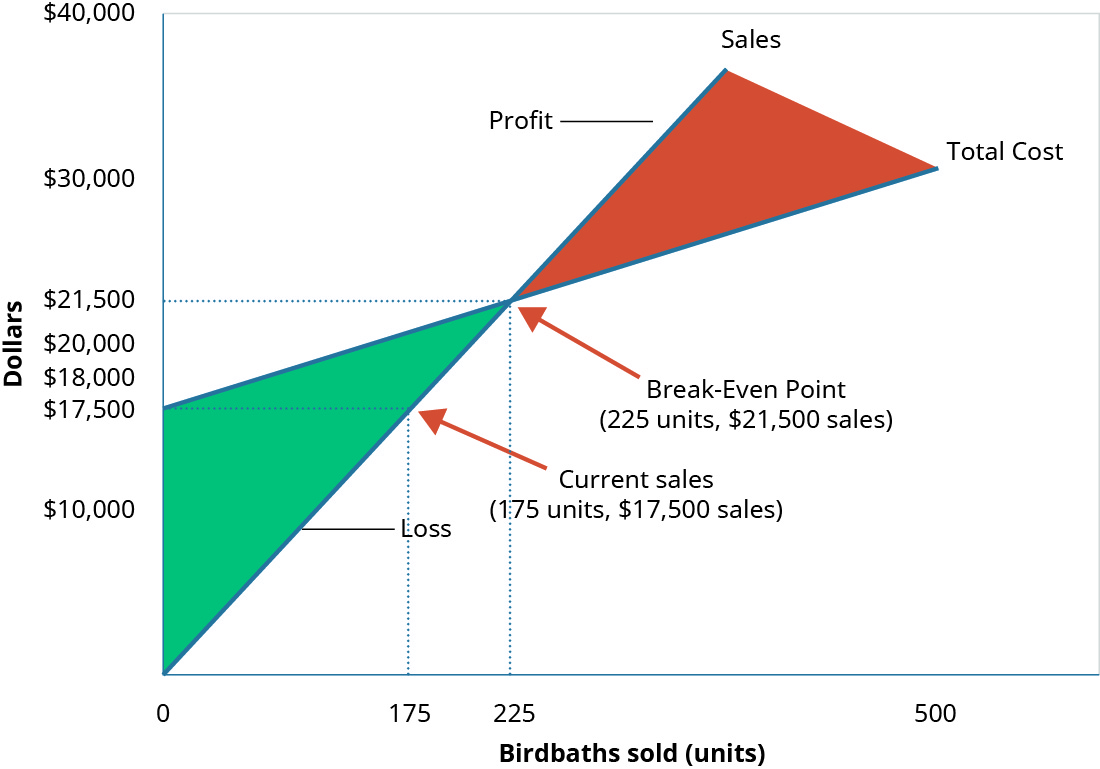
In a recent month, local flooding caused Hicks to close for several days, reducing the number of units they could ship and sell from \(225\) units to \(175\) units. The information in Figure \(\PageIndex{5}\) reflects this drop in sales.

At \(175\) units (\(\$17,500\) in sales), Hicks does not generate enough sales revenue to cover their fixed expenses and they suffer a loss of \(\$4,000\). They did not reach the break-even point of \(225\) units.
Sales Where Operating Income Is Positive
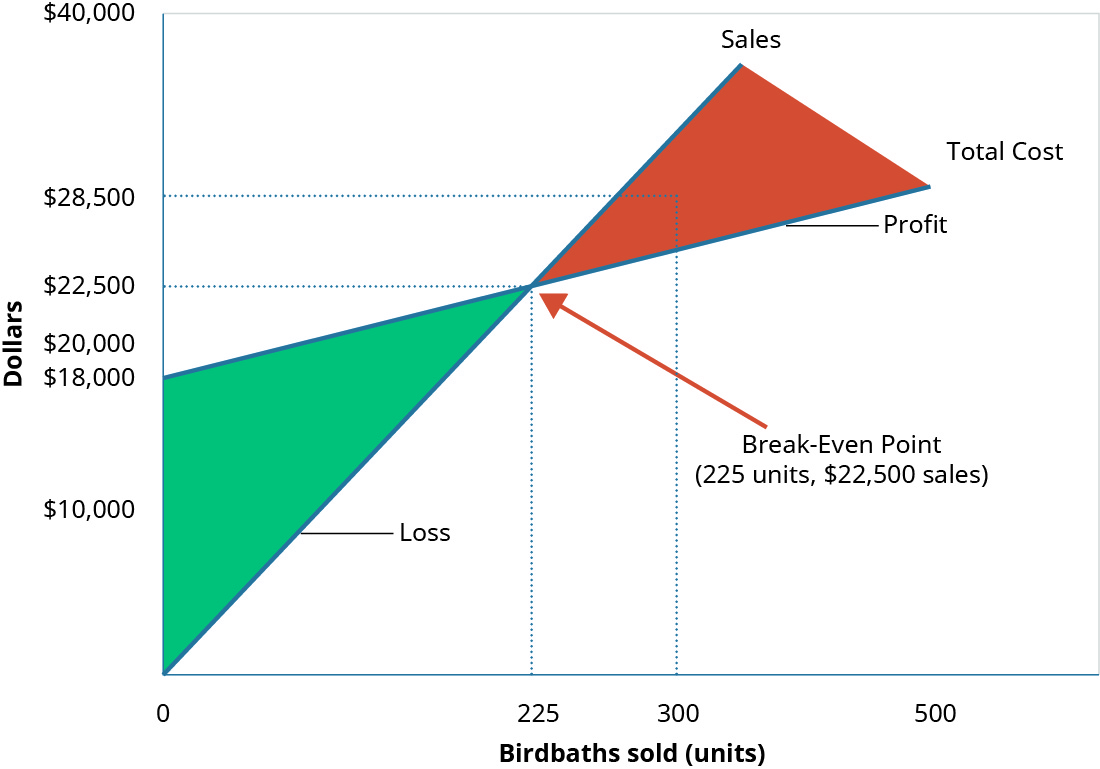
What happens when Hicks has a busy month and sells \(300\) Blue Jay birdbaths? We have already established that the contribution margin from \(225\) units will put them at break-even. When sales exceed the break-even point the unit contribution margin from the additional units will go toward profit. This is reflected on their income statement.

Again, looking at the graph for break-even (Figure \(\PageIndex{8}\)), you will see that their sales have moved them beyond the point where total revenue is equal to total cost and into the profit area of the graph.
Hicks Manufacturing can use the information from these different scenarios to inform many of their decisions about operations, such as sales goals.
However, using the contribution margin per unit is not the only way to determine a break-even point. Recall that we were able to determine a contribution margin expressed in dollars by finding the contribution margin ratio. We can apply that contribution margin ratio to the break-even analysis to determine the break-even point in dollars. For example, we know that Hicks had \(\$18,000\) in fixed costs and a contribution margin ratio of \(80\%\) for the Blue Jay model. We will use this ratio (Figure \(\PageIndex{9}\)) to calculate the break-even point in dollars.
\[\text { Break-Even Point in Dollars }=\dfrac{\text { Fixed Costs }}{\text { Contribution Margin Ratio }} \label{eq1}\]
Applying Equation \ref{eq1} to Hicks gives this calculation:
\[\dfrac{\$ 18,000}{0.80}=\$ 22,500 \nonumber \]
Hicks Manufacturing will have to generate \(\$22,500\) in monthly sales in order to cover all of their fixed costs. In order for us to verify that Hicks’ break-even point is \(\$22,500\) (or \(225\) units) we will look again at the contribution margin income statement at break-even:

By knowing at what level sales are sufficient to cover fixed expenses is critical, but companies want to be able to make a profit and can use this break-even analysis to help them.
You are the manager of a hair salon and want to know how many ladies’ haircuts your salon needs to sell in a month in order to cover the fixed costs of running the salon. You have determined that, at the current price of \(\$35\) per haircut, you have \(\$20\) in variable costs associated with each cut. These variable costs include stylist wages, hair product, and shop supplies. Your fixed costs are \(\$3,000\) per month. You perform a break-even analysis on a per-unit basis and discover the following:

You have \(4\) stylists plus yourself working in the salon and are open 6 days per week. Considering the break-even point and the number of available stylists, will the salon ever break even? If it does, what will need to happen? What can be done to achieve the break-even point?
Examples of the Effects of Variable and Fixed Costs in Determining the Break-Even Point
Companies typically do not want to simply break even, as they are in business to make a profit. Break-even analysis also can help companies determine the level of sales (in dollars or in units) that is needed to make a desired profit. The process for factoring a desired level of profit into a break-even analysis is to add the desired level of profit to the fixed costs and then calculate a new break-even point. We know that Hicks Manufacturing breaks even at \(225\) Blue Jay birdbaths, but what if they have a target profit for the month of July? They can simply add that target to their fixed costs. By calculating a target profit, they will produce and (hopefully) sell enough bird baths to cover both fixed costs and the target profit.
If Hicks wants to earn \(\$16,000\) in profit in the month of May, we can calculate their new break-even point as follows:
\[ \text { Target Profit }=\dfrac{\text { Fixed costs }+\text { desired profit }}{\text { Contribution margin per unit }}=\dfrac{\$ 18,000+\$ 16,000}{\$ 80}=425 \text { units } \nonumber \]
We have already established that the \(\$18,000\) in fixed costs is covered at the \(225\) units mark, so an additional \(200\) units will cover the desired profit (\(200\) units \(× \$80\) per unit contribution margin \(= \$16,000\)). Alternatively, we can calculate this in terms of dollars by using the contribution margin ratio.
\[ \text { Target Profit }=\dfrac{\text { Fixed costs }+\text { desired profit }}{\text { Contribution margin ratio }}=\dfrac{\$ 18,000+\$ 16,000}{0.80}=\$ 42,500 \nonumber \]
As done previously, we can confirm this calculation using the contribution margin income statement:

Note that the example calculations ignored income taxes, which implies we were finding target operating income. However, companies may want to determine what level of sales would generate a desired after-tax profit. To find the break-even point at a desired after-tax profit, we simply need to convert the desired after-tax profit to the desired pre-tax profit, also referred to as operating income, and then follow through as in the example. Suppose Hicks wants to earn \(\$24,000\) after-taxes, what level of sales (units and dollars) would be needed to meet that goal? First, the after-tax profit needs to be converted to a pre-tax desired profit:
\[ \text { Pre-tax desired profit }=\dfrac{\text { After-tax profit }}{(1-\text { tax rate })} \nonumber \]
If the tax rate for Hicks is \(40\%\), then the \(\$24,000\) after-tax profit is equal to a pre-tax profit of \(\$40,000\):
\[ \$ 40,000=\dfrac{\$ 24,000}{(1-0.40)} \nonumber \]
The tax rate indicates the amount of tax expense that will result from any profits and \(1-\text {tax rate}\) indicates the amount remaining after taking out tax expense. The concept is similar to buying an item on sale. If an item costs \(\$80\) and is on sale for \(40\%\) off, then the amount being paid for the item is \(60\%\) of the sale price, or \(\$ 48(\$ 80 \times 60 \%)\). Another way to find this involves two steps. First find the discount (\(\$80 × 40\% = \$32\)) and then subtract the discount from the sales price (\(\$80 – \$32 = \$48\)).
Taxes and profit work in a similar fashion. If we know the profit before tax is \(\$100,000\) and the tax rate is \(30\%\), then tax expenses are \(\$100,000 × 30\% = \$30,000\). This means the after-tax income is \(\$100,000 – \$30,000 = \$70,000\). However, in most break-even situations, as well as other decision-making areas, the desired after-tax profit is known, and the pre-tax profit must be determined by dividing the after-tax profit by \(1-\text {tax rate}\).
To demonstrate the combination of both a profit and the after-tax effects and subsequent calculations, let’s return to the Hicks Manufacturing example. Let’s assume that we want to calculate the target volume in units and revenue that Hicks must sell to generate an after-tax return of \(\$24,000\), assuming the same fixed costs of \(\$18,000\).
Since we earlier determined \(\$24,000\) after-tax equals \(\$40,000\) before-tax if the tax rate is \(40\%\), we simply use the break-even at a desired profit formula to determine the target sales.
\[\text { Target sales }=\dfrac{\text { (Fixed costs }+\text { Desired profit) }}{\text { Contribution margin per unit }}=\dfrac{(\$ 18,000+\$ 40,000)}{\$ 80}=725 \text { units } \nonumber \]
This calculation demonstrates that Hicks would need to sell \(725\) units at \(\$100\) a unit to generate \(\$72,500\) in sales to earn \(\$24,000\) in after-tax profits.
Alternatively, target sales in sales dollars could have been calculated using the contribution margin ratio:
\[\text { Target sales }=\dfrac{\text { (Fixed costs + Desired profit) }}{\text { Contribution margin per unit }}=\dfrac{(\$ 18,000+\$ 40,000)}{0.80}=\$ 72,500 \nonumber \]
Once again, the contribution margin income statement proves the sales and profit relationships.

Thus, to calculate break-even point at a particular after-tax income, the only additional step is to convert after-tax income to pre-tax income prior to utilizing the break-even formula. It is good to understand the impact of taxes on break-even analysis as companies will often want to plan based on the after-tax effects of a decision as the after-tax portion of income is the only part of income that will be available for future use.
Application of Break-Even Concepts for a Service Organization
Because break-even analysis is applicable to any business enterprise, we can apply these same principles to a service organization. For example, Marshall & Hirito is a mid-sized accounting firm that provides a wide range of accounting services to its clients but relies heavily on personal income tax preparation for much of its revenue. They have analyzed the cost to the firm associated with preparing these returns. They have determined the following cost structure for the preparation of a standard 1040A Individual Income Tax Return:

They have fixed costs of \(\$14,000\) per month associated with the salaries of the accountants who are responsible for preparing the Form 1040A. In order to determine their break-even point, they first determine the contribution margin for the Form 1040A as shown:

Now they can calculate their break-even point:
\[\text { Break-Even Point in Units }=\dfrac{\text { Total fixed costs }}{\text { Contribution margin per unit }}=\dfrac{\$ 14,000}{\$ 250}=56 \text { returns } \nonumber \]
Remember, this is the break-even point in units (the number of tax returns) but they can also find a break-even point expressed in dollars by using the contribution margin ratio. First, they find the contribution margin ratio. Then, they use the ratio to calculate the break-even point in dollars:
\[\text { Break-Even Point in Dollars }=\dfrac{\text { Fixed costs }}{\text { Contribution margin ratio }}=\dfrac{\$ 14,000}{0.625}=\$ 22,400 \nonumber \]
We can confirm these figures by preparing a contribution margin income statement:

Therefore, as long as Marshall & Hirito prepares \(56\) Form 1040 income tax returns, they will earn no profit but also incur no loss. What if Marshall & Hirito has a target monthly profit of \(\$10,000\)? They can use the break-even analysis process to determine how many returns they will need to prepare in order to cover their fixed expenses and reach their target profit:
\[\text { Target Profit }=\dfrac{\text { Fixed costs }+\text { desired profit }}{\text { Contribution margin per unit }}=\dfrac{\$ 14,000+\$ 10,000}{\$ 250}=96 \text { returns } \nonumber \]
They will need to prepare \(96\) returns during the month in order to realize a \(\$10,000\) profit. Expressing this in dollars instead of units requires that we use the contribution margin ratio as shown:
\[\text { Target Profit }=\dfrac{\text { Fixed costs }+\text { desired profit }}{\text { Contribution margin per unit }}=\dfrac{\$ 14,000+\$ 10,000}{0.625}=\$ 38,400 \nonumber \]
Marshall & Hirito now knows that, in order to cover the fixed costs associated with this service, they must generate \(\$38,400\) in revenue. Once again, let’s verify this by constructing a contribution margin income statement:

As you can see, the \(\$38,400\) in revenue will not only cover the \(\$14,000\) in fixed costs, but will supply Marshall & Hirito with the \(\$10,000\) in profit (net income) they desire.
As you’ve learned, break-even can be calculated using either contribution margin per unit or the contribution margin ratio. Now that you have seen this process, let’s look at an example of these two concepts presented together to illustrate how either method will provide the same financial results.
Suppose that Channing’s Chairs designs, builds, and sells unique ergonomic desk chairs for home and business. Their bestselling chair is the Spine Saver. Figure \(\PageIndex{18}\) illustrates how Channing could determine the break-even point in sales dollars using either the contribution margin per unit or the contribution margin ratio.
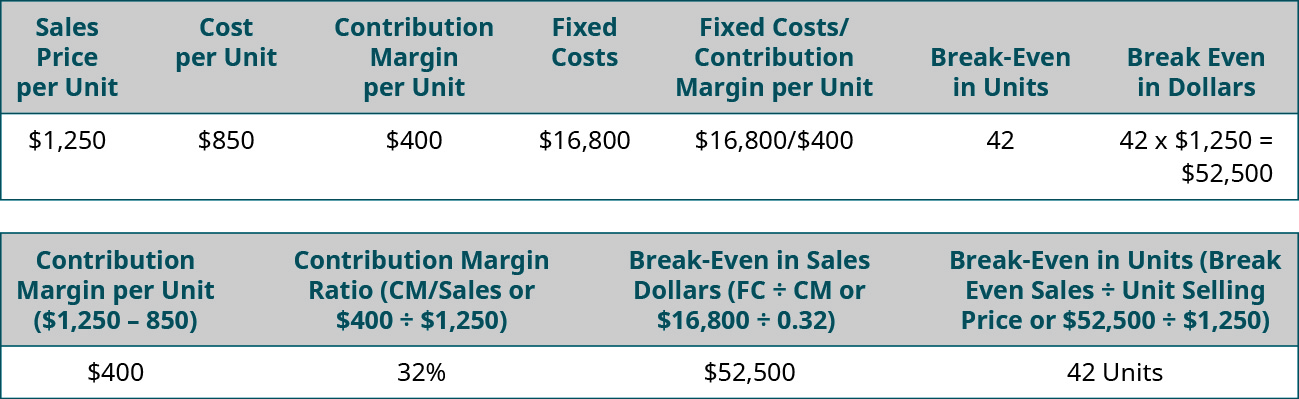
Note that in either scenario, the break-even point is the same in dollars and units, regardless of approach. Thus, you can always find the break-even point (or a desired profit) in units and then convert it to sales by multiplying by the selling price per unit. Alternatively, you can find the break-even point in sales dollars and then find the number of units by dividing by the selling price per unit.
College Creations, Inc (CC), builds a loft that is easily adaptable to most dorm rooms or apartments and can be assembled into a variety of configurations. Each loft is sold for \(\$500\), and the cost to produce one loft is \(\$300\), including all parts and labor. CC has fixed costs of \(\$100,000\).
- What happens if CC produces nothing?
- Now, assume CC produces and sells one unit (loft). What are their financial results?
- Now, what do you think would happen if they produced and sold 501 units?
- How many units would CC need to sell in order to break even?
- How many units would CC need to sell if they wanted to have a pretax profit of \(\$50,000\)?
Solution
- If they produce nothing, they will still incur fixed costs of \(\$100,000\). They will suffer a net loss of \(\$100,000\).
- If they sell one unit, they will have a net loss of \(\$99,800\).

- If they produce \(501\) units, they will have operating income of \(\$200\) as shown:

- Break-even can be determined by FC/CM per unit: \(\$ 100,000 \div \$ 200=500\). Five hundred lofts must be sold to break even.
- The desired profit can be treated like a fixed cost, and the target profit would be (FC + Desired Profit)/CM or (\(\$100,000 + \$50,000) ÷ \$200 = 750\). Seven hundred fifty lofts need to be sold to reach a desired income of \(\$50,000\). Another way to have found this is to know that, after fixed costs are met, the \(\$200\) per unit contribution margin will go toward profit. The desired profit of \(\$50,000 ÷ \$200 \text { per unit contribution margin } = 250\). This means that \(250\) additional units must be sold. To break even requires \(500\) units to be sold, and to reach the desired profit of \(\$50,000\) requires an additional \(250\) units, for a total of \(750\) units.


