8.4: The Internal Rate of Return
- Page ID
- 882
- Evaluate investments using the internal rate of return (IRR) approach.
Question: Using the internal rate of return (IRR) to evaluate investments is similar to using the net present value (NPV) in that both methods consider the time value of money. However, the IRR provides additional information that helps companies evaluate long-term investments. What is the IRR, and how does it help managers make decisions related to longterm investments?
- Answer
-
The internal rate of return (IRR)8 is the rate required (r) to get an NPV of zero for a series of cash flows. The IRR represents the time-adjusted rate of return for the investment being considered. The IRR decision rule states that if the IRR is greater than or equal to the company’s required rate of return (recall that this is often called the hurdle rate), the investment is accepted; otherwise, the investment is rejected.
Most managers use a spreadsheet, such as Excel, to calculate the IRR for an investment (we discuss this later in the chapter). However, we can also use trial and error to approximate the IRR. The goal is simply to find the rate that generates an NPV of zero. Let’s go back to the Jackson’s Quality Copies example. Figure 8.4 provides the projected cash flows for a new copy machine and the NPV calculation using a rate of 10 percent. Recall that the NPV was $1,250, indicating the investment generates a return greater than the company’s required rate of return of 10 percent.
Although it is useful to know that the investment’s return is greater than the company’s required rate of return, managers often want to know the exact return generated by the investment. (It is often not enough to state that the exact return is something higher than 10 percent!) Managers also like to rank investment opportunities by the return each investment is expected to generate. Our goal now is to determine the exact return—that is, to determine the IRR. We know from Figure 8.4 that the copy machine investment generates a return greater than 10 percent. Figure 8.5 summarizes this calculation with the 2 columns under the 10 percent heading.
The far right side of Figure 8.5 shows that the NPV is $(2,100) if the rate is increased to 12 percent (recall our goal is to find the rate that yields an NPV of 0). Thus the IRR is between 10 and 12 percent. Next, we try 11 percent. As shown in the middle of Figure 8.5, 11 percent provides an NPV of $(469). Thus the IRR is between 10 and 11 percent; it is closer to 11 percent because $(469) is closer to 0 than $1,250. (Note that as the rate increases, the NPV decreases, and as the rate decreases, the NPV increases.)
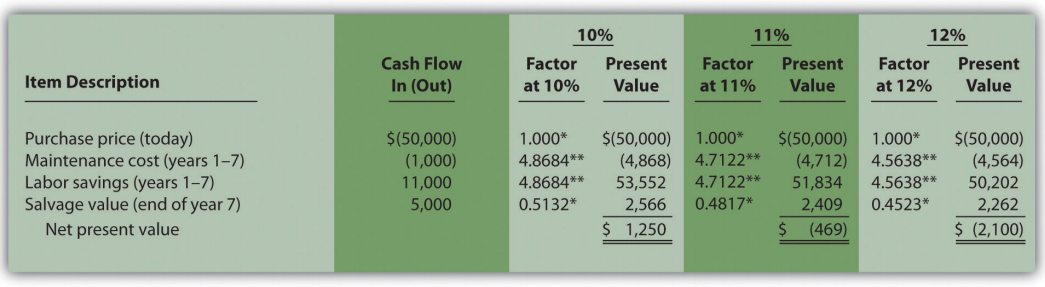
Figure \(\PageIndex{5}\): - Finding the IRR for Jackson’s Quality Copies *Because this is not an annuity, use Figure 8.9 in the appendix.
**Because this is an annuity, use Figure 8.10 in the appendix. The number of years (n) equals seven since identical cash flows occur each year for seven years.
Note: the NPV of $(469) is closest to 0. Thus the IRR is close to 11 percent.
This trial and error approach allows us to approximate the IRR. As stated earlier, if the IRR is greater than or equal to the company’s required rate of return, the investment is accepted; otherwise, the investment is rejected. For Jackson’s Quality Copies, the IRR of approximately 11 percent is greater than the company’s required rate of return of 10 percent. Thus the investment should be accepted.
Using Excel to Calculate NPV and IRR
Let’s use the Jackson’s Quality Copies example presented at the beginning of the chapter to illustrate how Excel can be used to calculate the NPV and IRR. Two steps are required to calculate the NPV and IRR using Excel. All cell references are to the following spreadsheet shown.
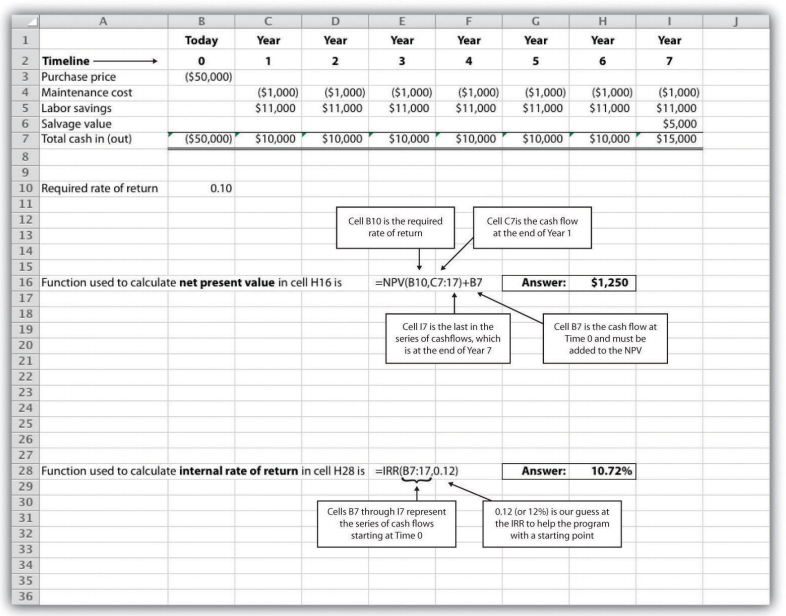
Step 1. Enter the data in the spreadsheet.
Rows 1 through 7 in the spreadsheet show the cash flows associated with the proposal to purchase a new copy machine at Jackson’s Quality Copies (first presented in Figure 8.1).
Step 2. Input the functions to calculate NPV and IRR.
We selected cell H16 to calculate the NPV, so this is where the NPV function is input. Cell E16 shows the function in detail with dialogue boxes provided for clarification. Notice that the resulting NPV of $1,250 shown in cell H16 is the same as the NPV calculated in Figure 8.2 and Figure 8.4.
We selected cell H28 to calculate the IRR, so this is where the IRR function is input. Cell E28 shows the function in detail. Notice that the resulting IRR of 10.72 percent shown in cell H28 is very close to our approximation of slightly less than 11 percent shown in Figure 8.5.
As an alternative to entering a function directly into the spreadsheet, the NPV function under the Formulas menu in Excel can be used. Simply select the cell in the spreadsheet where you would like the answer to appear (H16 in this case), and go to the Formulas menu. Click on the fx symbol or Insert Function on the formula bar. Search for the function by typing in NPV, select NPV where it appears in the box, then select OK. When asked for the Rate, enter the cell where the rate appears (B10). Then under Value 1 enter the cells containing the series of cash flows, starting with year 1 (shown as C7:I7, which means C7 through I7). Select OK. Now go back and add the cash flow at time 0 (B7) to the end of the NPV function. The resulting formula will look like the formula shown in E16, and the answer will appear in the cell where the function is entered (H16).
The IRR function can be inserted into a cell using the same process presented previously. Select the cell in the spreadsheet where you would like the answer to appear (H28), and go to the Formulas menu. Click on the fx symbol or Insert Function on the formula bar. Search for the function by typing in IRR, select IRR where it appears in the box below, then select OK. When asked for Values, enter the cells containing the series of cash flows, starting with time 0 (shown as B7:I7, which means B7 through I7). When asked for a Guess, enter your best guess as to what the IRR might be (this provides the system with a starting point), then select OK. The resulting formula will look like the formula shown in E28, and the answer will appear in the cell where the function is entered (H28).
The IRR is the rate required (r) to get an NPV of zero for a series of cash flows and represents the time-adjusted rate of return for an investment. If the IRR is greater than or equal to the company’s required rate of return (often called the hurdle rate), the investment is accepted; otherwise, the investment is rejected.
This review problem is a continuation of Note 8.17 "Review Problem 8.2", and uses the same information. The management of Chip Manufacturing, Inc., would like to purchase a specialized production machine for $700,000. The machine is expected to have a life of 4 years, and a salvage value of $100,000. Annual maintenance costs will total $30,000. Annual labor and material savings are predicted to be $250,000. The company’s required rate of return is 15 percent.
- Based on your answer to Note 8.17 "Review Problem 8.2", use trial and error to approximate the IRR for this investment proposal.
- Should Chip Manufacturing, Inc., purchase the specialized production machine? Explain.
- Answer
-
- In Note 8.17 "Review Problem 8.2", the NPV was calculated using 15 percent (the company’s required rate of return). Knowing that 15 percent results in an NPV of $(14,720), and therefore seeing the return is less than 15 percent, we decreased the rate to 13 percent. As shown in the following figure, this resulted in an NPV of $15,720, which indicates the return is higher than 13 percent. Using a rate of 14 percent results in an NPV very close to 0 at $224. Thus the IRR is close to 14 percent.
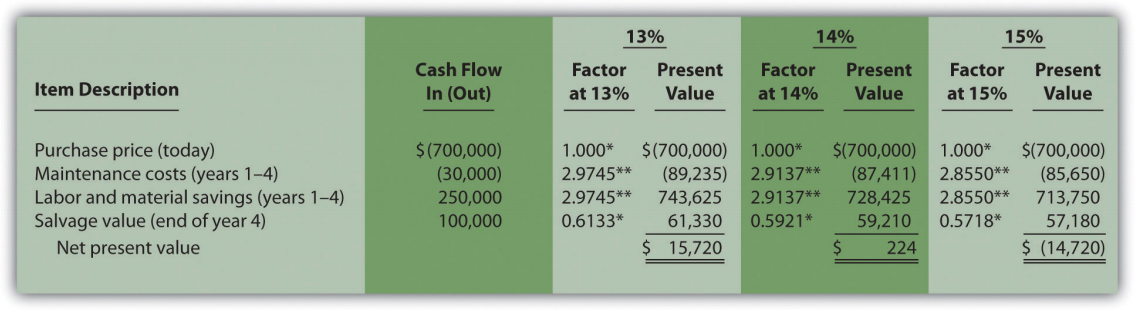
*Because this is not an annuity, use Figure 8.9 in the appendix.
**Because this is an annuity, use Figure 8.10 in the appendix. The number of years (n) equals four since identical cash flows occur each year for four years. - Because the IRR of 14 percent is less than the company’s required rate of return of 15 percent, Chip Manufacturing, Inc., should not purchase the specialized production machine.
- In Note 8.17 "Review Problem 8.2", the NPV was calculated using 15 percent (the company’s required rate of return). Knowing that 15 percent results in an NPV of $(14,720), and therefore seeing the return is less than 15 percent, we decreased the rate to 13 percent. As shown in the following figure, this resulted in an NPV of $15,720, which indicates the return is higher than 13 percent. Using a rate of 14 percent results in an NPV very close to 0 at $224. Thus the IRR is close to 14 percent.
Definition
- A method used to evaluate long-term investments. It is defined as the rate required to get a net present value of zero for a series of cash flows.


