17.12: Macroeconomic Effects of Exchange Rates
- Page ID
- 48540
Learning Objectives
- Explain how changes in exchange rates influence aggregate demand and supply
Exchange Rates, Aggregate Demand, and Aggregate Supply
A central bank will be concerned about the exchange rate for three reasons: (1) Movements in the exchange rate will affect the quantity of aggregate demand in an economy; (2) frequent substantial fluctuations in the exchange rate can disrupt international trade and cause problems in a nation’s banking system; (3) the exchange rate may contribute to an unsustainable balance of trade and large inflows of international financial capital, which can set the economy up for a deep recession if international investors decide to move their money to another country. Let’s discuss these scenarios in turn.
Foreign trade in goods and services typically involves incurring the costs of production in one currency while receiving revenues from sales in another currency. As a result, movements in exchange rates can have a powerful effect on incentives to export and import, and thus on aggregate demand in the economy as a whole.
For example, in 1999, when the euro first became a currency, its value measured in U.S. currency was $1.06/euro. By the end of 2013, the euro had risen (and the U.S. dollar had correspondingly weakened) to $1.37/euro. Consider the situation of a French firm that each year incurs €10 million in costs, and sells its products in the United States for $10 million. In 1999, when this firm converted $10 million back to euros at the exchange rate of $1.06/euro (that is, $10 million × [€1/$1.06]), it received €9.4 million, and suffered a loss. In 2013, when this same firm converted $10 million back to euros at the exchange rate of $1.37/euro (that is, $10 million × [€1 euro/$1.37]), it received approximately €7.3 million and an even larger loss. This example shows how a stronger euro discourages exports by the French firm, because it makes the costs of production in the domestic currency higher relative to the sales revenues earned in another country. From the point of view of the U.S. economy, the example also shows how a weaker U.S. dollar encourages exports.
Since an increase in exports results in more dollars flowing into the economy, and an increase in imports means more dollars are flowing out, it is easy to conclude that exports are “good” for the economy and imports are “bad,” but this overlooks the role of exchange rates. If an American consumer buys a Japanese car for $20,000 instead of an American car for $30,000, it may be tempting to argue that the American economy has lost out. However, the Japanese company will have to convert those dollars to yen to pay its workers and operate its factories. Whoever buys those dollars will have to use them to purchase American goods and services, so the money comes right back into the American economy. At the same time, the consumer saves money by buying a less expensive import, and can use the extra money for other purposes.
Watch It
This video reviews some of the concepts you’ve already learned about the foreign exchange market and also provides a good example of how the appreciation or depreciation of money impacts imports and exports.
Fluctuations in Exchange Rates
Exchange rates can fluctuate a great deal in the short run. From February 2008 to March 2009, the Indian rupee moved from 39 rupees/dollar ito 51 rupees/dollar, a decline of more than one-fourth in the value of the rupee on foreign exchange markets. We read earlier that even two economically developed neighboring economies like the United States and Canada can see significant movements in exchange rates over a few years. For firms that depend on export sales, or firms that rely on imported inputs to production, or even purely domestic firms that compete with firms tied into international trade—which in many countries adds up to half or more of a nation’s GDP—sharp movements in exchange rates can lead to dramatic changes in profits and losses. So, a central bank may desire to keep exchange rates from moving too much as part of providing a stable business climate, where firms can focus on productivity and innovation, not on reacting to exchange rate fluctuations.
One of the most economically destructive effects of exchange rate fluctuations can happen through the banking system. Most international loans are measured in a few large currencies, like U.S. dollars, European euros, and Japanese yen. In countries that do not use these currencies, banks often borrow funds in the currencies of other countries, like U.S. dollars, but then lend in their own domestic currency. The left-hand chain of events in Figure 1 shows how this pattern of international borrowing can work. A bank in Thailand borrows one million U.S. dollars. Then the bank converts the dollars to its domestic currency—in the case of Thailand, the currency is the baht—at a rate of 40 baht/dollar. The bank then lends the baht to a firm in Thailand. The business repays the loan in baht, and the bank converts it back to U.S. dollars to pay off its original U.S. dollar loan.
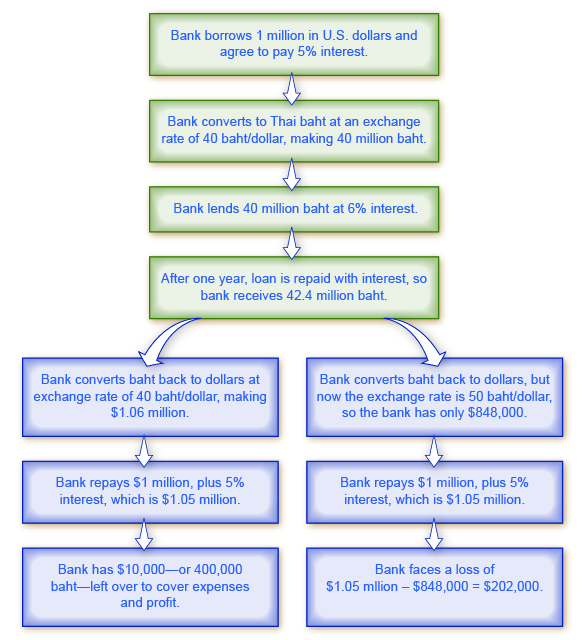
This process of borrowing in a foreign currency and lending in a domestic currency can work just fine, as long as the exchange rate does not shift. In the scenario outlined, if the dollar strengthens and the baht weakens, a problem arises. The right-hand chain of events in Figure 1 illustrates what happens when the baht unexpectedly weakens from 40 baht/dollar to 50 baht/dollar. The Thai firm still repays the loan in full to the bank. But because of the shift in the exchange rate, the bank cannot repay its loan in U.S. dollars. (Of course, if the exchange rate had changed in the other direction, making the Thai currency stronger, the bank could have realized an unexpectedly large profit.)
In 1997–1998, countries across eastern Asia, like Thailand, Korea, Malaysia, and Indonesia, experienced a sharp depreciation of their currencies, in some cases 50% or more. These countries had been experiencing substantial inflows of foreign investment capital, with bank lending increasing by 20% to 30% per year through the mid-1990s. When their exchange rates depreciated, the banking systems in these countries became bankrupt. Argentina experienced a similar chain of events in 2002. When the Argentine peso depreciated, Argentina’s banks found themselves unable to pay back what they had borrowed in U.S. dollars.
Banks play a vital role in any economy in facilitating transactions and in making loans to firms and consumers. When most of a country’s largest banks become bankrupt simultaneously, a sharp decline in aggregate demand and a deep recession results. Since the main responsibilities of a central bank are to control the money supply and to ensure that the banking system is stable, a central bank must be concerned about whether large and unexpected exchange rate depreciation will drive most of the country’s existing banks into bankruptcy.
Contributors and Attributions
- Modification, adaptation, and original content. Provided by: Lumen Learning. License: CC BY: Attribution
- Macroeconomic Effects of Exchange Rates. Authored by: OpenStax College. Located at: https://cnx.org/contents/vEmOH-_p@4.44:-oE69rDB@2/Macroeconomic-Effects-of-Excha. License: CC BY: Attribution. License Terms: Download for free at http://cnx.org/content/col11626/latest
- (Macro) Episode 33: Exchange Rates. Authored by: Dr. Mary J. McGlasson. Located at: https://www.youtube.com/watch?v=xwtgByffoUw&t=308s. License: CC BY-NC-ND: Attribution-NonCommercial-NoDerivatives

