8.16: The Foundations of the Demand Curve
- Page ID
- 48384
Learning Objectives
- Describe how demand curves are derived from consumer equilibrium
In this module, we’ve learned how consumers spend their limited income in order to maximize total utility. Each consumer choice problem yields a consumer equilibrium, showing the combination of goods and services an individual chooses to purchase with their budget, given the individual’s preferences and given the prices of the goods and services available.
Remember that a demand curve shows the relationship between price of a product and quantity demanded. While demand curves will appear somewhat different for each product – they may appear relatively steep or flat, straight or curved – demand curves slope down from left to right. So demand curves embody the law of demand: as the price increases, the quantity demanded decreases, and conversely, as the price decreases, the quantity demanded increases.
In this section, we explore the relationship between consumer equilibrium and demand curves.
Demand Curves
Figure 1 shows a budget constraint with a choice between housing and “everything else.” (Putting “everything else” on the vertical axis can be a useful approach in some cases, especially when the focus of the analysis is on one particular good.) We label the consumer equilibrium, M0. This consumer equilibrium was found by applying the two rules used to maximize utility explained earlier.
Consider how changes in the price of a good affect the budget constraint and the consumer equilibrium. An increase in the price of housing will not change the quantity of “everything else” that the consumer is able to buy. If the consumer were to spend their entire budget on “everything else,” they could still afford the amount shown by the vertical axis of the budget constraint. But it will reduce the amount of housing the consumer can purchase. Thus, if the price of housing increases, the budget constraint will rotate towards the horizontal axis. This is shown in Figure 2 below.
The other three budget constraints represent successively higher prices for housing of P1, P2, and P3. As the budget constraint rotates in, and in, and in again, we label the utility-maximizing choices M1, M2, and M3, and the quantity demanded of housing falls from Q0 to Q1 to Q2 to Q3.
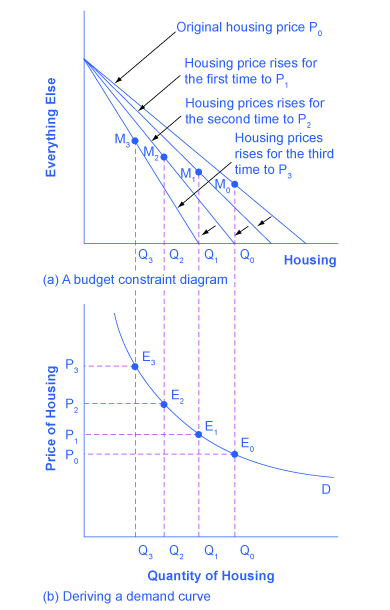
So, as the price of housing rises, the budget constraint rotates clockwise (inward), and the quantity consumed of housing falls, ceteris paribus (meaning, with all other things being the same). This relationship—the price of housing rising from P0 to P1 to P2 to P3, while the quantity of housing demanded falls from Q0 to Q1 to Q2 to Q3—is graphed on the demand curve in Figure 2(b). Indeed, the vertical dashed lines stretching between the top and bottom of Figure 1 show that the quantity of housing demanded at each point is the same in both (a) and (b). Thus, the shape of a demand curve is ultimately determined by the underlying choices about maximizing utility subject to a budget constraint. And while economists may not be able to measure “utils,” they can certainly measure price and quantity demanded.
Applications in Government and Business
The budget constraint framework for making utility-maximizing choices offers a reminder that people can react to a change in price or income in a range of different ways. For example, in the winter months of 2005, costs for heating homes increased significantly in many parts of the country as prices for natural gas and electricity soared, due in large part to the disruption caused by Hurricanes Katrina and Rita. Some people reacted by reducing the quantity demanded of energy; for example, by turning down the thermostats in their homes by a few degrees and wearing a heavier sweater inside. Even so, many home heating bills rose, so people adjusted their consumption in other ways, too. As you learned in the module on Elasticity, the short run demand for home heating is generally inelastic. Each household cut back on what it valued least on the margin; for some it might have been some dinners out, or a vacation, or postponing buying a new refrigerator or a new car. Indeed, sharply higher energy prices can have effects beyond the energy market, leading to a widespread reduction in purchasing throughout the rest of the economy.
A similar issue arises when the government imposes taxes on certain products, like it does on gasoline, cigarettes, and alcohol. Say that a tax on alcohol leads to a higher price at the liquor store, the higher price of alcohol causes the budget constraint to pivot left, and consumption of alcoholic beverages is likely to decrease. However, people may also react to the higher price of alcoholic beverages by cutting back on other purchases. For example, they might cut back on snacks at restaurants like chicken wings and nachos. It would be unwise to assume that the liquor industry is the only one affected by the tax on alcoholic beverages.
Does it make a difference who controls household income?
In the mid-1970s, the United Kingdom made an interesting policy change in its “child allowance” policy. This program provides a fixed amount of money per child to every family, regardless of family income. Traditionally, the child allowance had been distributed to families by withholding less in taxes from the paycheck of the family wage earner—typically the father in this time period. The new policy instead provided the child allowance as a cash payment to the mother. As a result of this change, households have the same level of income and face the same prices in the market, but the money is more likely to be in the purse of the mother than in the wallet of the father.
Should this change in policy alter household consumption patterns? Basic models of consumption decisions, of the sort examined in this module, assume that it does not matter whether the mother or the father receives the money, because both parents seek to maximize the utility of the family as a whole. In effect, this model assumes that everyone in the family has the same preferences.
In reality, the share of income controlled by the father or the mother does affect what the household consumes. When the mother controls a larger share of family income a number of studies, in the United Kingdom and in a wide variety of other countries, have found that the family tends to spend more on restaurant meals, child care, and women’s clothing, and less on alcohol and tobacco. As the mother controls a larger share of household resources, children’s health improves, too. These findings suggest that when providing assistance to poor families, in high-income countries and low-income countries alike, the monetary amount of assistance is not all that matters: it also matters which member of the family actually receives the money.
The budget constraint framework serves as a constant reminder to think about the full range of effects that can arise from changes in income or price, not just effects on the one product that might seem most immediately affected.
- How Changes in Income and Prices Affect Consumption Choices. Authored by: OpenStax College. Located at: https://cnx.org/contents/vEmOH-_p@4.17:cCMVAG8i@4/How-Changes-in-Income-and-Pric. License: CC BY: Attribution. License Terms: Download for free at http://cnx.org/contents/bc498e1f-efe...569ad09a82@4.4

