6.2: Least Squares Regression Method

Last updated
Save as PDF

Page ID: 45859

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Learning Outcomes

Use the least-squares regression method to create a regression line on a graph of cost data

This method uses all of the data available to separate the fixed and variable portions of a mixed cost. A regression line is fitted into the data using the following formula:

Y= a + bX

Y= Maintenance costs

X= Number of dogs groomed

a= the total fixed cost

b= the variable cost per unit of activity

So using a calculator available HERE.

If you use the data from the dog groomer example you should be able to calculate the following chart:

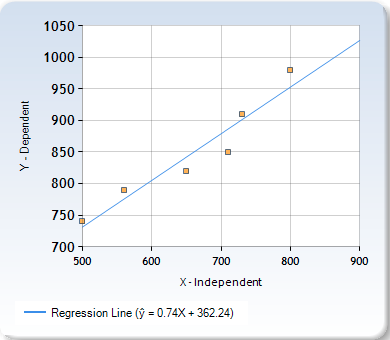
A graph depicting a regression line with "independent" on the x-axis and "dependent" on the y-axis. The graph is trending in a linear progression.

This method is more accurate, using all of the available data. The table below shows the difference in calculation using the two methods:

Costs	High-low	Least Squares Regression Method
Variable cost estimate per dog groomed	$.080	$.074
Fixed cost estimate per month	$340	$362.24

Practice Questions

https://assessments.lumenlearning.co...sessments/9603

Least Squares Regression Method. Authored by: Freedom Learning Group. Provided by: Lumen Learning. License: CC BY: Attribution