3: How Is Cost-Volume-Profit Analysis Used for Decision Making?
- Page ID
- 51391
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Recilia Vera is vice president of sales at Snowboard Company, a manufacturer of one model of snowboard. Lisa Donley is the company accountant. Recilia and Lisa are in their weekly meeting.
Recilia:
Lisa, I’m in the process of setting up an incentive system for my sales staff, and I’d like to get a better handle on our financial information.
Lisa:
No problem. How can I help?
Recilia:
I’ve reviewed our financial results for the past 12 months. It looks like we made a profit in some months, and had losses in other months. From what I can tell, we sell each snowboard for $250, our variable cost is $150 per unit, and our fixed cost is $75 per unit. It seems to me that if we sell just one snowboard each month, we should still show a profit of $25, and any additional units sold should increase total profit.
Lisa:
Your unit sales price of $250 and unit variable cost of $150 look accurate to me, but I’m not sure about your unit fixed cost of $75. Fixed costs total $50,000 a month regardless of the number of units we produce. Trying to express fixed costs on a per unit basis can be misleading because it depends on the number of units being produced and sold, which changes each month. I can tell you that each snowboard produced and sold provides $100 toward covering fixed costs—that is, $250, the sales price of one snowboard, minus $150 in variable cost.
Recilia:
The $75 per unit for fixed costs was my estimate based on last year’s sales, but I get your point. As you know, I’d like to avoid having losses. Is it possible to determine how many units we have to sell each month to at least cover our expenses? I’d also like to discuss what it will take to make a decent profit.
Lisa:
We can certainly calculate how many units have to be sold to cover expenses, and I’d be glad to discuss how many units must be sold to make a decent profit.
Recilia:
Excellent! Let’s meet again next week to go through this in detail.
Answering questions regarding break-even and target profit points requires an understanding of the relationship among costs, volume, and profit (often called CVP). This chapter discusses cost-volume-profit analysis, which identifies how changes in key assumptions (for example, assumptions related to cost, volume, or profit) may impact financial projections. We address Recilia’s questions in the next section.
3.1 Cost-Volume-Profit Analysis for Single-Product Companies
Learning Objective
- Perform cost-volume-profit analysis for single-product companies.
Question: The profit equation shows that profit equals total revenues minus total variable costs and total fixed costs. This profit equation is used extensively in cost-volume-profit (CVP) analysis, and the information in the profit equation is typically presented in the form of a contribution margin income statement (first introduced in Chapter 2 “How Do Organizations Identify Cost Behavior Patterns?”). What is the relationship between the profit equation and the contribution margin income statement?
Answer: Recall that the contribution margin income statement starts with sales, deducts variable costs to determine the contribution margin, and deducts fixed costs to arrive at profit. We use the term “variable cost” because it describes a cost that varies in total with changes in volume of activity. We use the term “fixed cost” because it describes a cost that is fixed (does not change) in total with changes in volume of activity.
To allow for a mathematical approach to performing CVP analysis, the contribution margin income statement is converted to an equation using the following variables:
Key Equation
S = Selling price per unit
V = Variable cost per unit
F = Total fixed costs
Q = Quantity of units produced and sold
Thus
Profit=Total sales−Total variable costs−Total fixed costs or Profit=(S×Q)−(V×Q)−F
Figure 3.1 “Comparison of Contribution Margin Income Statement with Profit Equation” clarifies the link between the contribution margin income statement presented in Chapter 2 “How Do Organizations Identify Cost Behavior Patterns?” and the profit equation stated previously. Study this figure carefully because you will encounter these concepts throughout the chapter.
Figure 3.1 Comparison of Contribution Margin Income Statement with Profit Equation

Recall that when identifying cost behavior patterns, we assume that management is using the cost information to make short-term decisions. Variable and fixed cost concepts are useful for short-term decision making. The short-term period varies, depending on a company’s current production capacity and the time required to change capacity. In the long term, all cost behavior patterns could change.
Break-Even and Target Profit
Question: Companies such as Snowboard Company often want to know the sales required to break even, which is called the break-even point. What is meant by the term break-even point?
Answer: The break-even point can be described either in units or in sales dollars. The break-even point in units is the number of units that must be sold to achieve zero profit. The break-even point in sales dollars is the total sales measured in dollars required to achieve zero profit. If a company sells products or services easily measured in units (e.g., cars, computers, or mountain bikes), then the formula for break-even point in units is used. If a company sells products or services not easily measured in units (e.g., restaurants, law firms, or electricians), then the formula for break-even point in sales dollars is used.
Break-Even Point in Units
Question: How is the break-even point in units calculated, and what is the break-even point for Snowboard Company?
Answer: The break-even point in units is found by setting profit to zero using the profit equation. Once profit is set to zero, fill in the appropriate information for selling price per unit (S), variable cost per unit (V), and total fixed costs (F), and solve for the quantity of units produced and sold (Q).
Let’s calculate the break-even point in units for Snowboard Company. Recall that each snowboard sells for $250. Unit variable costs total $150, and total monthly fixed costs are $50,000. To find the break-even point in units for Snowboard Company, set the profit to zero, insert the unit sales price (S), insert the unit variable cost (V), insert the total fixed costs (F), and solve for the quantity of units produced and sold (Q):
Profit=(S×Q)−(V×Q)−F=($250 x Q)−($150 x Q) −$50,000=0
100 x Q – $50,000 = 0
100 x Q = $50,000
Q = 50,000/100 = 500 units
Short cut formula is Fixed Costs / Contribution Margin per unit = Break Even point in units
Contribution margin per unit is Sales price per unit less variable costs per unit.
Thus Snowboard Company must produce and sell 500 snowboards to break even. This answer is confirmed in the following contribution margin income statement.

Target Profit in Units
Question: Although it is helpful for companies to know the break-even point, most organizations are more interested in determining the sales required to make a targeted amount of profit. How does finding the target profit in units help companies like Snowboard Company?
Answer: Finding a target profit in units. simply means that a company would like to know how many units of product must be sold to achieve a certain profit. At Snowboard Company, Recilia (the vice president of sales) and Lisa (the accountant) are in their next weekly meeting.
Lisa:
Recilia, last week you asked how many units we have to sell to cover our expenses. This is called the break-even point. If each unit produced and sold provides $100 toward covering fixed costs, and if total monthly fixed costs are $50,000, we would have to sell 500 units to break even—that is, $50,000 divided by $100.
Recilia:
What happens once we sell enough units to cover all of our fixed costs for the month?
Lisa:
Good question! Once all fixed costs are covered for the month, each unit sold contributes $100 toward profit.
Recilia:
I think I’m getting the hang of this. It will take 500 units in sales to break even, and each unit sold above 500 results in a $100 increase in profit. So if we sell 503 units for a month, profit will total $300?
Lisa:
You’ve got it!
Recilia:
So if our goal is to make a profit of $30,000 per month (target profit), how many units must be sold?
Lisa:
It takes 500 units to break even. We also know each unit sold above and beyond 500 units contributes $100 toward profit. Thus we would have to sell an additional 300 units above the break-even point to earn a profit of $30,000. This means we would have to sell 800 units in total to make $30,000 in profit.
Recilia:
Wow, I’m not sure selling 800 units is realistic, but at least we have a better sense of what needs to be done to make a decent profit. Thanks for your help!
Profit Equation
Question: Let’s formalize this discussion by using the profit equation. How is the profit equation used to find a target profit amount in units?
Answer: Finding the target profit in units is similar to finding the break-even point in units except that profit is no longer set to zero. Instead, set the profit to the target profit the company would like to achieve. Then fill in the information for selling price per unit (S), variable cost per unit (V), and total fixed costs (F), and solve for the quantity of units produced and sold (Q):
Profit=(S×Q)−(V×Q)−F =$30,000
=($250 x Q)−($150 x Q)−$50,000 = $30,000
=$100x Q−$50,000 = $30,000
=$100 x Q = $80,000
Q=800 units
Thus Snowboard Company must produce and sell 800 snowboards to achieve $30,000 in profit. This answer is confirmed in the following contribution margin income statement:

Shortcut Formula
Question: Although using the profit equation to solve for the break-even point or target profit in units tends to be the easiest approach, we can also use a shortcut formula derived from this equation. What is the shortcut formula, and how is it used to find the target profit in units for Snowboard Company?
Answer: The shortcut formula is as follows:
Break-Even Point in Sales Dollars
Question: Finding the break-even point in units works well for companies that have products easily measured in units, such as snowboard or bike manufacturers, but not so well for companies that have a variety of products not easily measured in units, such as law firms and restaurants. How do companies find the break-even point if they cannot easily measure sales in units?
Answer: For these types of companies, the break-even point is measured in sales dollars. That is, we determine the total revenue (total sales dollars) required to achieve zero profit for companies that cannot easily measure sales in units.
Finding the break-even point in sales dollars requires the introduction of two new terms: contribution margin per unit and contribution margin ratio.
Contribution Margin per Unit
The contribution margin per unit is the amount each unit sold contributes to (1) covering fixed costs and (2) increasing profit. We calculate it by subtracting variable costs per unit (V) from the selling price per unit (S).
Key Equation
Contribution margin per unit = S − V
For Snowboard Company the contribution margin is $100:
Contribution margin per unit=S−V or $100=$250−$150
Thus each unit sold contributes $100 to covering fixed costs and increasing profit.
Contribution Margin Ratio
The contribution margin ratio measures the amount each sales dollar contributes to (1) covering fixed costs and (2) increasing profit; also called contribution margin percent. The contribution margin ratio is the contribution margin per unit divided by the selling price per unit. (Note that the contribution margin ratio can also be calculated using the total contribution margin and total sales; the result is the same.)
Key Equation
Contribution margin ratio = (S − V) ÷ S
For Snowboard Company the contribution margin ratio is 40 percent:
Contribution margin ratio=(S − V)÷S 40%=($250 − $150)÷$250
Thus each dollar in sales contributes 40 cents ($0.40) to covering fixed costs and increasing profit.
Question: With an understanding of the contribution margin and contribution margin ratio, we can now calculate the break-even point in sales dollars. How do we calculate the break-even point in sales dollars for Snowboard Company?
Answer: The formula to find the break-even point in sales dollars is as follows.
Key Equation
Break-even point in sales dollars= Total fixed costs / Contribution margin ratio
For Snowboard Company the break-even point in sales dollars is $125,000 per month:
Break-even point in sales dollars=$50,000 / .4 or 40% = $125,000 in sales=$50,000 / .40
Thus Snowboard Company must achieve $125,000 in total sales to break even. The following contribution margin income statement confirms this answer:

Target Profit in Sales Dollars
Key Equation
Target profit in sales dollars = (Total fixed costs + Target profit) / Contribution margin ratio
Question: Finding a target profit in sales dollars simply means that a company would like to know total sales measured in dollars required to achieve a certain profit. Finding the target profit in sales dollars is similar to finding the break-even point in sales dollars except that “target profit” is no longer set to zero. Instead, target profit is set to the profit the company would like to achieve. Recall that management of Snowboard Company asked the following question: What is the amount of total sales dollars required to earn a target profit of $30,000?
Answer: Use the break-even formula described in the previous section. Instead of setting the target profit to $0, set it to $30,000. This results in an answer of $200,000 in monthly sales:
Target profit in sales dollars=(Total fixed costs + Target profit) / Contribution margin ratio or $200,000 in sales=($50,000+$30,000) / 0.40
Thus Snowboard Company must achieve $200,000 in sales to make $30,000 in monthly profit. The following contribution margin income statement confirms this answer:

Business in Action 3.1
See the podcast for a visual representation of how breakeven may be considered at Southwest Airlines.
CVP Graph
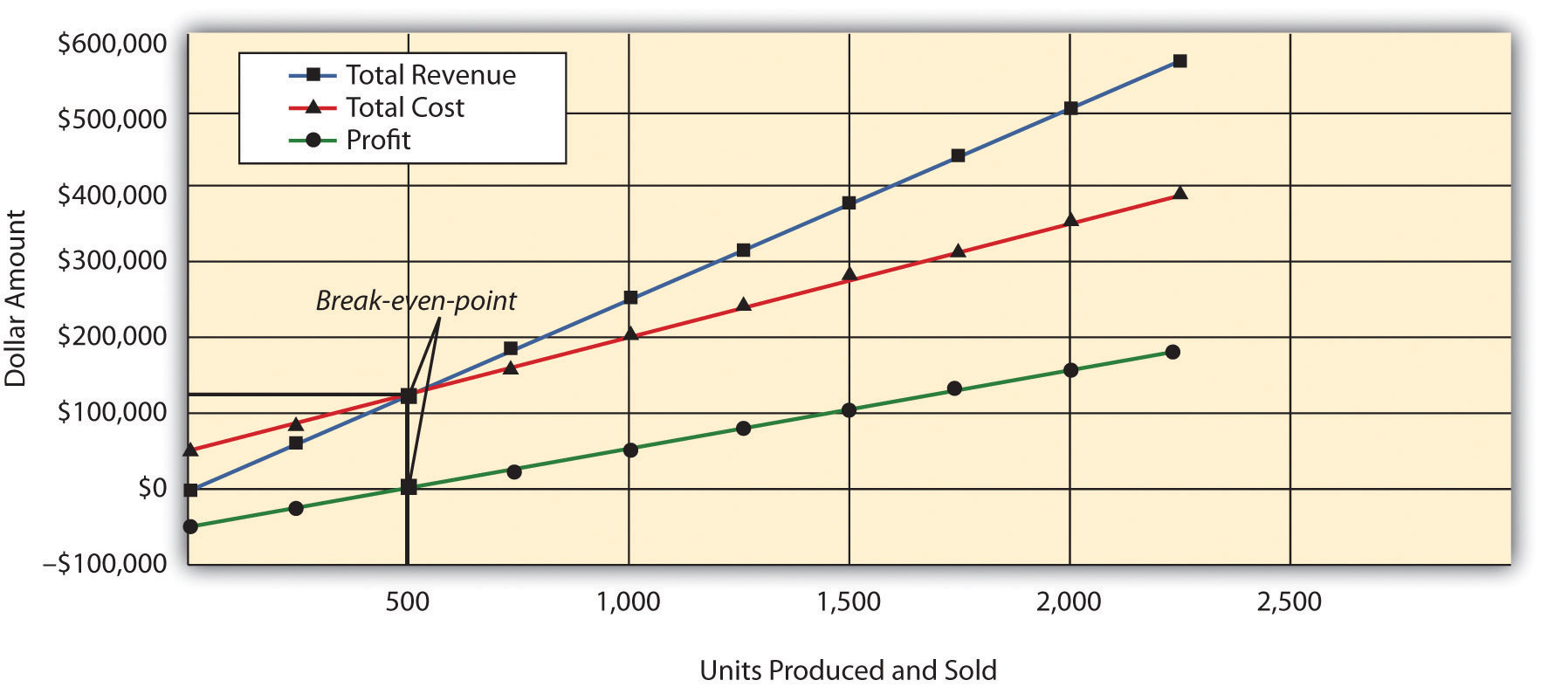
Question: The relationship of costs, volume, and profit can be displayed in the form of a graph. What does this graph look like for Snowboard Company, and how does it help management evaluate financial information related to the production of snowboards?
Answer: Figure 3.2 “CVP Graph for Snowboard Company” shows in graph form the relationship between cost, volume, and profit for Snowboard Company. The vertical axis represents dollar amounts for revenues, costs, and profits. The horizontal axis represents the volume of activity for a period, measured as units produced and sold for Snowboard.
There are three lines in the graph:
- Total revenue
- Total cost
- Profit
The total revenue line shows total revenue based on the number of units produced and sold. For example, if Snowboard produces and sells one unit, total revenue is $250 (= 1 × $250). If it produces and sells 2,000 units, total revenue is $500,000 (= 2,000 × $250).
The total cost line shows total cost based on the number of units produced and sold. For example, if Snowboard produces and sells one unit, total cost is $50,150 [= $50,000 + (1 × $150)]. If it produces and sells 2,000 units, total cost is $350,000 [= $50,000 + (2,000 × $150)].
The profit line shows profit or loss based on the number of units produced and sold. It is simply the difference between the total revenue and total cost lines. For example, if Snowboard produces and sells 2,000 units, the profit is $150,000 (= $500,000 − $350,000). If no units are sold, a loss is incurred equal to total fixed costs of $50,000.
Figure 3.2 CVP Graph for Snowboard Company
Margin of Safety
Question: Managers often like to know how close projected sales are to the break-even point. How is this information calculated and used by management?
Answer: The excess of projected sales over the break-even point is called the margin of safety. The margin of safety represents the amount by which sales can fall before the company incurs a loss.
Key Equation
Margin of safety (in units) = Projected sales (in units) − Break-even sales (in units)
Assume Snowboard Company expects to sell 700 snowboards and that its break-even point is 500 units; the margin of safety is 200 units. The calculation is
Margin of safety (in units)=Projected sales (in units)−Break-even sales (in units) 200=700−500
Thus sales can drop by 200 units per month before the company begins to incur a loss.
The margin of safety can also be stated in sales dollars.
Key Equation
Margin of safety (in sales $) = Projected sales (in sales $) − Break-even sales (in sales $)
For Snowboard the margin of safety in sales dollars is $50,000:
Margin of safety (in sales $)=Projected sales (in sales $)−Break-even sales (in sales $) $50,000=(700 units×$250)−(500 units×$250)
Thus sales revenue can drop by $50,000 per month before the company begins to incur a loss.
Key Takeaway
-
Cost-volume-profit analysis involves finding the break-even and target profit point in units and in sales dollars. The key formulas for an organization with a single product are summarized in the following list. Set the target profit to $0 for break-even calculations, or to the appropriate profit dollar amount for target profit calculations. The margin of safety formula is also shown:
-
Break-even or target profit point measured in units:
(Total fixed costs + Target profit) / (Selling price per unit − Variable cost per unit)
(The denominator is also called “contribution margin per unit.”)
-
Break-even or target profit point measured in sales dollars:
Total fixed costs + Target profit / Contribution margin ratio
-
Margin of safety in units or sales dollars:
Projected sales − Break-even sales
-
Check Yourself
Star Symphony would like to perform for a neighboring city. Fixed costs for the performance total $5,000. Tickets will sell for $15 per person, and an outside organization responsible for processing ticket orders charges the symphony a fee of $2 per ticket. Star Symphony expects to sell 500 tickets.
- How many tickets must Star Symphony sell to break even?
- How many tickets must the symphony sell to earn a profit of $7,000?
- How much must Star Symphony have in sales dollars to break even?
- How much must Star Symphony have in sales dollars to earn a profit of $7,000?
- What is the symphony’s margin of safety in units and in sales dollars?
Solution:
Note: All solutions are rounded.
-
The symphony must sell 385 tickets to break even:
(Total fixed costs + Target profit) / (Selling price per unit − Variable cost per unit)=($5,000+$0) / ($15−$2)=385 tickets (rounded)
-
The symphony must sell 923 tickets to make a profit of $7,000:
(Total fixed costs + Target profit) / (Selling price per unit − Variable cost per unit)= ($5,000+$7,000) / ($15−$2) = 923 tickets (rounded)
-
The symphony must make $5,769 in sales to break even:
(Total fixed costs + Target profit) / Contribution margin ratio=($5,000+$0) / (($15−$2) ÷$15) = $5,769 (rounded)
-
The symphony must make $13,846 in sales to earn a profit of $7,000:
(Total fixed costs + Target profit) / Contribution margin ratio= ($5,000+$7,000) / (($15−$2) ÷$15)=$13,846 (rounded)
-
The symphony’s margin of safety is 115 units or $1,725 in sales:
Margin of safety=Projected sales − Break-even sales 115 tickets=500 tickets−385 tickets $1,725 in sales=(500×$15)−(385×$15)
3.2 Cost-Volume-Profit Analysis for Multiple-Product and Service Companies
Learning Objectives
- Perform cost-volume-profit analysis for multiple-product and service companies.
Question: Although the previous section illustrated cost-volume-profit (CVP) analysis for companies with a single product easily measured in units, most companies have more than one product or perhaps offer services not easily measured in units. Suppose you are the manager of a company called Kayaks-For-Fun that produces two kayak models, River and Sea. What information is needed to calculate the break-even point for this company?
Answer: The following information is required to find the break-even point:
- Monthly fixed costs total $24,000.
- The River model represents 60 percent of total sales volume and the Sea model accounts for 40 percent of total sales volume.
- The unit selling price and variable cost information for the two products follow:

Finding the Break-Even Point and Target Profit in Units for Multiple-Product Companies
Question: Given the information provided for Kayaks-For-Fun, how will the company calculate the break-even point?
Answer: First, we must expand the profit equation presented earlier to include multiple products. The following terms are used once again. However, subscript r identifies the River model, and subscript s identifies the Sea model (e.g., Sr stands for the River model’s selling price per unit). CM is new to this section and represents the contribution margin.
Key Equation
S = Selling price per unit
V = Variable cost per unit
F = Total fixed costs
Q = Quantity of units produced and sold
CM = Contribution margin
Thus
Profit=Total sales−Total variable costs−Total fixed costs = Profit
=[(Sr ×Qr)+(Ss ×Qs)]−[(Vr ×Qr)+(Vs ×Qs)]−F
Without going through a detailed derivation, this equation can be restated in a simplified manner for Kayaks-For-Fun, as follows:
Profit=(Unit CM for River×Quantity of River)+(Unit CM for Sea×Quantity of Sea)−F
Profit=$400 x Qr+$150 x Qs − $24,000
One manager at Kayaks-For-Fun believes the break-even point should be 60 units in total, and another manager believes the break-even point should be 160 units in total. Which manager is correct? The answer is both might be correct. If only the River kayak is produced and sold, 60 units is the break-even point. If only the Sea kayak is produced and sold, 160 units is the break-even point. There actually are many different break-even points, because the profit equation has two unknown variables, Qr and Qs.
Profit ($0) = ($400 × 30 units of River) + ($150 × 80 units of Sea) − $24,000
Profit ($0) = ($400 × 35 units of River) + ($150 × 67 units of Sea) − $24,000
Profit ($0) = ($400 × 40 units of River) + ($150 × 53 units of Sea) − $24,000
Break-Even Point in Units and the Weighted Average Contribution Margin per Unit
Question: Because most companies sell multiple products that have different selling prices and different variable costs, the break-even or target profit point depends on the sales mix. What is the sales mix, and how is it used to calculate the break-even point?
Answer: The sales mix is the proportion of one product’s sales to total sales. In the case of Kayaks-For-Fun, the River model accounts for 60 percent of total unit sales and the Sea model accounts for 40 percent of total unit sales.
In calculating the break-even point for Kayaks-For-Fun, we must assume the sales mix for the River and Sea models will remain at 60 percent and 40 percent, respectively, at all different sales levels. The formula used to solve for the break-even point in units for multiple-product companies is similar to the one used for a single-product company, with one change. Instead of using the contribution margin per unit in the denominator, multiple-product companies use a weighted average contribution margin per unit. The formula to find the break-even point in units is as follows.
Key Equation
Total fixed costs + Target profit / Weighted average contribution margin per unit
When a company assumes a constant sales mix, a weighted average contribution margin per unit can be calculated by multiplying each product’s unit contribution margin by its proportion of total sales. The resulting weighted unit contribution margins for all products are then added together.
At Kayaks-For-Fun, the weighted average contribution margin per unit of $300 is
$300 = ($400 × 60 percent) + ($150 × 40 percent)
We can now determine the break-even point in units by using the following formula:
Break-even point in units=(Total fixed costs + Target profit) / Weighted average contribution margin per unit
Break-even point in units=($24,000+$0) / $300=80 total kayaks
Kayaks-For-Fun must sell 48 River models (= 60 percent × 80 units) and 32 Sea models (= 40 percent × 80 units) to break even. Again, this assumes the sales mix remains the same at different levels of sales volume.
Target Profit in Units
Question: We now know how to calculate the break-even point in units for a company with multiple products. How do we extend this process to find the target profit in units for a company with multiple products?
Answer: Finding the target profit in units for a company with multiple products is similar to finding the break-even point in units except that profit is no longer set to zero. Instead, profit is set to the target profit the company would like to achieve.
Key Equation
Target profit in units=(Total fixed costs + Target profit) / Weighted average contribution margin per unit
For example, assume Kayaks-For-Fun would like to know how many units it must sell to make a monthly profit of $96,000. Simply set the target profit to $96,000 and run the calculation:
Target profit in units=(Total fixed costs + Target profit) / Weighted average contribution margin per unit
Target profit in units=($24,000+$96,000)/$300=400 total kayaks
Kayaks-For-Fun must sell 240 River models (= 60 percent × 400) and 160 Sea models (= 40 percent × 400) to make a profit of $96,000.
Check Yourself
International Printer Machines (IPM) builds three computer printer models: Inkjet, Laser, and Color Laser. Information for these three products is as follows:
| Inkjet | Laser | Color Laser | Total | |
| Selling price per unit | $250 | $400 | $1,600 | |
| Variable cost per unit | $100 | $150 | $ 800 | |
| Expected unit sales (annual) | 12,000 | 6,000 | 2,000 | 20,000 |
| Sales mix | 60 percent | 30 percent | 10 percent | 100 percent |
Total annual fixed costs are $5,000,000. Assume the sales mix remains the same at all levels of sales.
-
- How many printers in total must be sold to break even?
- How many units of each printer must be sold to break even?
Solution:
Note: All solutions are rounded.
-
-
IPM must sell 20,408 printers to break even:
(Total fixed costs + Target profit) / Weighted average contribution margin per unit
Contribution margin for each product is sales price less variable cost per unit
Weighted Average Contribution Margin = ($150×0.60)+($250×0.30)+($800×0.10)= 245
-
($5,000,000 + 0) / $245=20,408 total units
2. As calculated previously, 20,408 printers must be sold to break even. Using the sales mix provided, the following number of units of each printer must be sold to break even:
-
-
- Inkjet: 12,245 units=20,408 × 0.60
- Laser: 6,122 units=20,408 × 0.30
- Color laser: 2,041 units=20,408 × 0.10
-
Break-Even Point in Sales Dollars and the Weighted Average Contribution Margin Ratio
Question: For companies that have unique products not easily measured in units, how do we find the break-even point?
Answer: Rather than measuring the break-even point in units, a more practical approach for these types of companies is to find the break-even point in sales dollars. We can use the formula that follows to find the break-even point in sales dollars for organizations with multiple products or services. Note that this formula is similar to the one used to find the break-even point in sales dollars for an organization with one product, except that the contribution margin ratio now becomes the weighted average contribution margin ratio.
Key Equation
Break-even point in sales dollars=(Total fixed costs + Target profit) / Weighted average contribution margin ratio
For example, suppose Amy’s Accounting Service has three departments—tax, audit, and consulting—that provide services to the company’s clients. Figure 3.4 “Income Statement for Amy’s Accounting Service” shows the company’s income statement for the year. Amy, the owner, would like to know what sales are required to break even. Note that fixed costs are known in total, but Amy does not allocate fixed costs to each department.
Figure 3.4 Income Statement for Amy’s Accounting Service
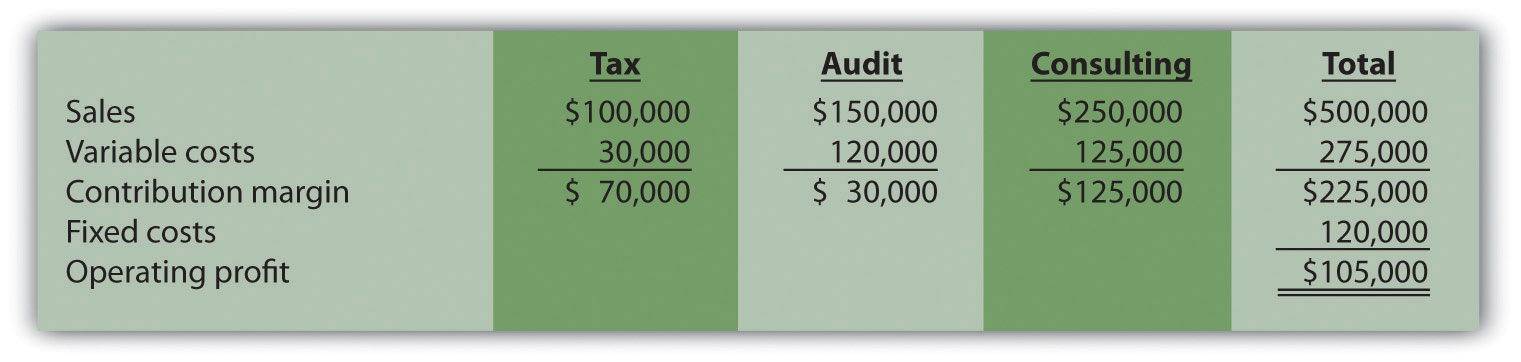
The contribution margin ratio differs for each department:
| Tax | 70 percent (= $70,000 ÷ $100,000) |
| Audit | 20 percent (= $30,000 ÷ $150,000) |
| Consulting | 50 percent (= $125,000 ÷ $250,000) |
Question: We have the contribution margin ratio for each department, but we need it for the company as a whole. How do we find the contribution margin ratio for all of the departments in the company combined?
Answer: The contribution margin ratio for the company as a whole is the weighted average contribution margin ratio. We calculate it by dividing the total contribution margin by total sales. For Amy’s Accounting Service, the weighted average contribution margin ratio is 45 percent (= $225,000 ÷ $500,000). For every dollar increase in sales, the company will generate an additional 45 cents ($0.45) in profit. This assumes that the sales mix remains the same at all levels of sales. (The sales mix here is measured in sales dollars for each department as a proportion of total sales dollars.)
Now that you know the weighted average contribution margin ratio for Amy’s Accounting Service, it is possible to calculate the break-even point in sales dollars:
Break-even point in sales dollars=(Total fixed costs + Target profit) / Weighted average contribution margin ratio
Break-even point in sales dollars=$120,000 / .45 =$266,667 (rounded)
Amy’s Accounting Service must achieve $266,667 in sales to break even.The weighted average contribution margin ratio can also be found by multiplying each department’s contribution margin ratio by its proportion of total sales. The resulting weighted average contribution margin ratios for all departments are then added. The calculation for Amy’s Accounting Service is as follows:45 percent weighted average contribution margin ratio = (tax has 20 percent of total sales × 70 percent contribution margin ratio) + (audit has 30 percent of total sales × 20 percent contribution margin ratio) + (consulting has 50 percent of total sales × 50 percent contribution margin ratio)Thus 45 percent = 14 percent + 6 percent + 25 percent.
Target Profit in Sales Dollars
Question: How do we find the target profit in sales dollars for companies with products not easily measured in units?
Answer: Finding the target profit in sales dollars for a company with multiple products or services is similar to finding the break-even point in sales dollars except that profit is no longer set to zero. Instead, profit is set to the target profit the company would like to achieve.
Key Equation
Target profit in sales dollars= (Total fixed costs + Target profit) / Weighted average contribution margin ratio
For example, assume Amy’s Accounting Service would like to know sales dollars required to make $250,000 in annual profit. Simply set the target profit to $250,000 and run the calculation:
Target profit in sales dollars=(Total fixed costs + Target profit) / Weighted average contribution margin ratio
Target profit in sales dollars=($120,000+$250,000) / 0.45=$822,222 (rounded)
Amy’s Accounting Service must achieve $822,222 in sales to earn $250,000 in profit.
Important Assumptions
Question: Several assumptions are required to perform break-even and target profit calculations for companies with multiple products or services. What are these important assumptions?
Answer: These assumptions are as follows:
- Costs can be separated into fixed and variable components.
- Contribution margin ratio remains constant for each product, segment, or department.
- Sales mix remains constant with changes in total sales.
These assumptions simplify the CVP model and enable accountants to perform CVP analysis quickly and easily. However, these assumptions may not be realistic, particularly if significant changes are made to the organization’s operations. When performing CVP analysis, it is important to consider the accuracy of these simplifying assumptions. It is always possible to design a more accurate and complex CVP model. But the benefits of obtaining more accurate data from a complex CVP model must outweigh the costs of developing such a model.
Key Takeaways
-
The key formula used to calculate the break-even or target profit point in units for a company with multiple products is as follows. Simply set the target profit to $0 for break-even calculations, or to the appropriate profit dollar amount for target profit calculations.
Total fixed costs + Target profit / Weighted average contribution margin per unit
-
The formula used to find the break-even point or target profit in sales dollars for companies with multiple products or service is as follows. Simply set the “Target Profit” to $0 for break-even calculations, or to the appropriate profit dollar amount for target profit calculations:
Total fixed costs + Target profit / Weighted Average contribution margin ratio
Check Yourself
Ott Landscape Incorporated provides landscape maintenance services for three types of clients: commercial, residential, and sports fields. Financial projections for this coming year for the three segments are as follows:

Assume the sales mix remains the same at all levels of sales.
- How much must Ott Landscape have in total sales dollars to break even?
- How much must Ott Landscape have in total sales dollars to earn an annual profit of $1,500,000?
Solution:
-
Sales of $1,000,000 are required to break even:
(Total fixed costs + Target profit) / Weighted average contribution margin ratio*=$200,000+$0 / 0.20=$1,000,000 in sales
*Weighted average contribution margin ratio = $1,000,000 ÷ $5,000,000 = 20 percent or 0.20.
-
Sales of $8,500,000 are required to make a profit of $1,500,000:
(Total fixed costs + Target profit) / Weighted average contribution margin ratio=($200,000+$1,500,000) / 0.20=$8,500,000 in sales
3.3 Using Cost-Volume-Profit Models for Sensitivity Analysis
Learning Objectives
- Use sensitivity analysis to determine how changes in the cost-volume-profit equation affect profit.
Question: We can use the cost-volume-profit (CVP) financial model described in this chapter for single-product, multiple-product, and service organizations to perform sensitivity analysis, also called what-if analysis. How is sensitivity analysis used to help managers make decisions?
Answer: Sensitivity analysis shows how the CVP model will change with changes in any of its variables (e.g., changes in fixed costs, variable costs, sales price, or sales mix). The focus is typically on how changes in variables will alter profit.
Sensitivity Analysis: An Example
To illustrate sensitivity analysis, let’s go back to Snowboard Company, a company that produces one snowboard model. The assumptions for Snowboard were as follows:
| Sales price per unit | $ 250 |
| Variable cost per unit | 150 |
| Fixed costs per month | 50,000 |
| Target profit | 30,000 |
Recall from earlier calculations that the break-even point is 500 units, and Snowboard must sell 800 units to achieve a target profit of $30,000. Management believes a goal of 800 units is overly optimistic and settles on a best guess of 700 units in monthly sales. This is called the “base case.” The base case is summarized as follows in contribution margin income statement format:

Question: Although management believes the base case is reasonably accurate, it is concerned about what will happen if certain variables change. As a result, you are asked to address the following questions from management (you are now performing sensitivity analysis!). Each scenario is independent of the others. Unless told otherwise, assume that the variables used in the base case remain the same. How do you answer the following questions for management?
- How will profit change if the sales price increases by $25 per unit (10 percent)?
- How will profit change if sales volume decreases by 70 units (10 percent)?
- How will profit change if fixed costs decrease by $15,000 (30 percent) and variable cost increases $15 per unit (10 percent)?
Answer: The CVP model shown in Figure 3.5 “Sensitivity Analysis for Snowboard Company” answers these questions. Each column represents a different scenario, with the first column showing the base case and the remaining columns providing answers to the three questions posed by management. The top part of Figure 3.5 “Sensitivity Analysis for Snowboard Company” shows the value of each variable based on the scenarios presented previously, and the bottom part presents the results in contribution margin income statement format.
Figure 3.5 Sensitivity Analysis for Snowboard Company
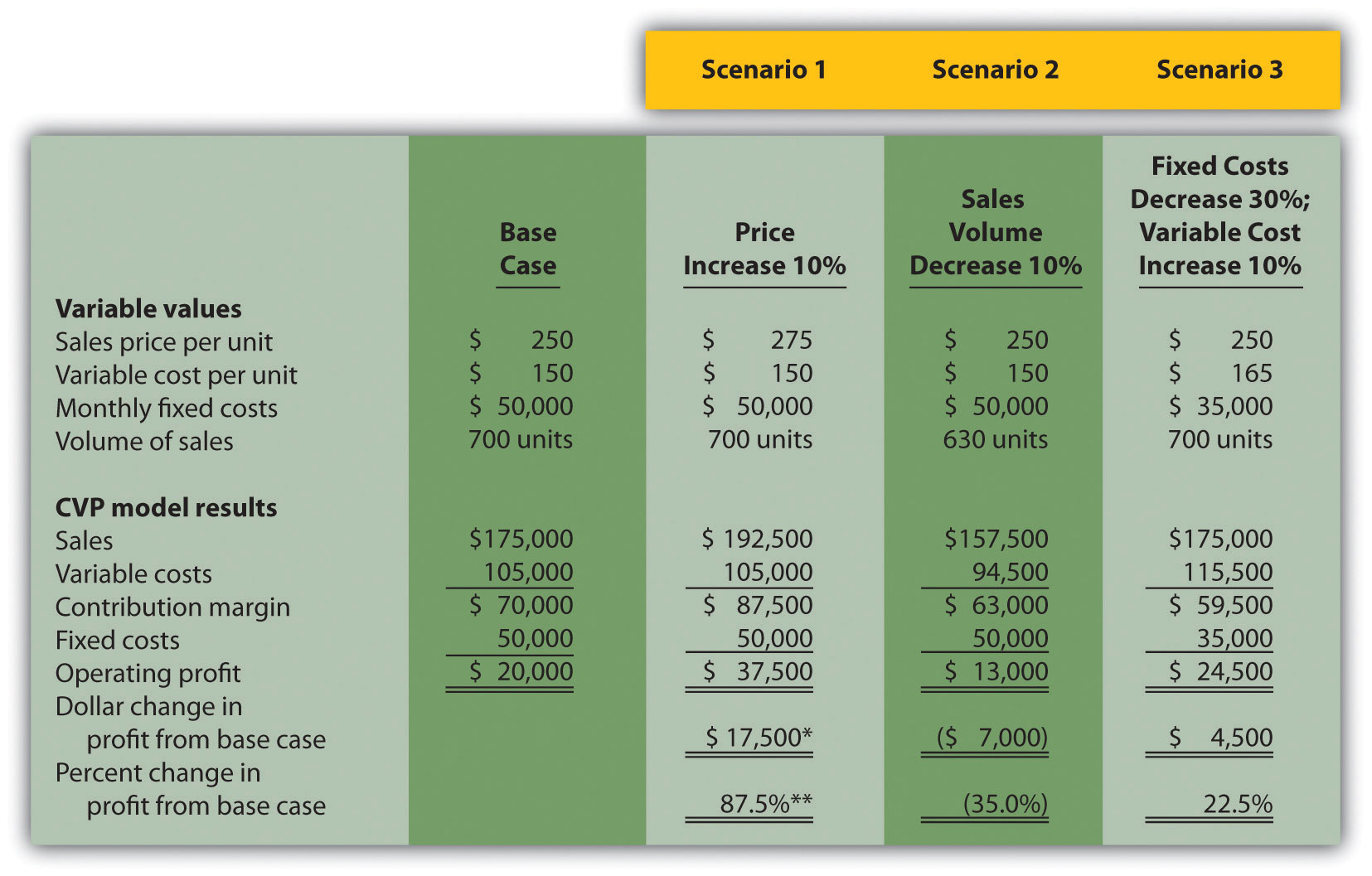
a $17,500 = $37,500 − $20,000.
b 87.5 percent = $17,500 ÷ $20,000.
Carefully review Figure 3.5 “Sensitivity Analysis for Snowboard Company”. The column labeled Scenario 1 shows that increasing the price by 10 percent will increase profit 87.5 percent ($17,500). Thus profit is highly sensitive to changes in sales price. Another way to look at this is that for every one percent increase in sales price, profit will increase by 8.75 percent, or for every one percent decrease in sales price, profit will decrease by 8.75 percent.
The column labeled Scenario 2 shows that decreasing sales volume 10 percent will decrease profit 35 percent ($7,000). Thus profit is also highly sensitive to changes in sales volume. Stated another way, every one percent decrease in sales volume will decrease profit by 3.5 percent; or every one percent increase in sales volume will increase profit by 3.5 percent.
When comparing Scenario 1 with Scenario 2, we see that Snowboard Company’s profit is more sensitive to changes in sales price than to changes in sales volume, although changes in either will significantly affect profit.
The column labeled Scenario 3 shows that decreasing fixed costs by 30 percent and increasing variable cost by 10 percent will increase profit 22.5 percent ($4,500). (Perhaps Snowboard Company is considering moving toward less automation and more direct labor!)
Computer Application
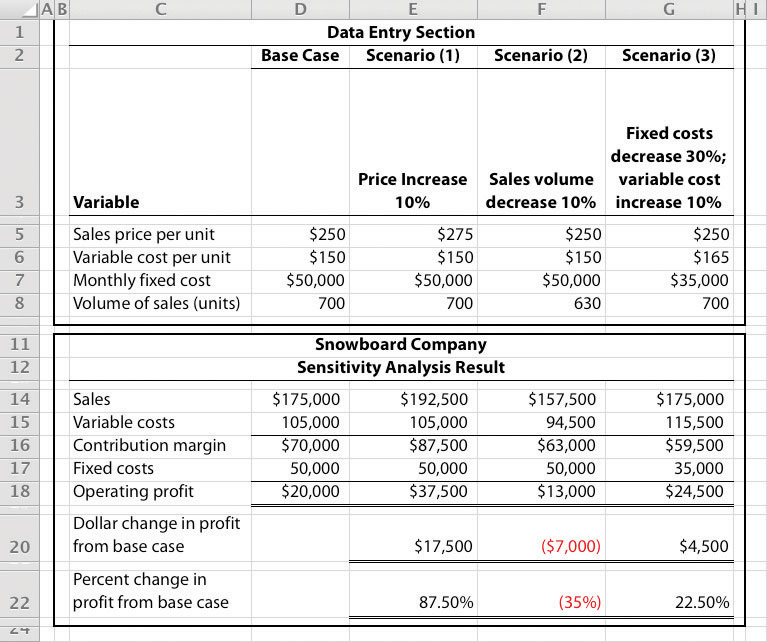
Using Excel to Perform Sensitivity Analysis
The accountants at Snowboard Company would likely use a spreadsheet program, such as Excel, to develop a CVP model for the sensitivity analysis shown in Figure 3.5 “Sensitivity Analysis for Snowboard Company”. An example of how to use Excel to prepare the CVP model shown in Figure 3.5 “Sensitivity Analysis for Snowboard Company” is presented as follows. Notice that the basic data are entered at the top of the spreadsheet (data entry section), and the rest of the information is driven by formulas. This allows for quick sensitivity analysis of different scenarios.
Using the base case as an example, sales of $175,000 (cell D14) are calculated by multiplying the $250 sales price per unit (cell D5) by 700 units (cell D8). Variable costs of $105,000 (cell D15) are calculated by multiplying the $150 variable cost per unit (cell D6) by 700 units (cell D8). Fixed costs of $50,000 come from the top section (cell D7). The contribution margin of $70,000 is calculated by subtracting variable costs from sales, and profit of $20,000 is calculated by subtracting fixed costs from the contribution margin.
Expanding the Use of Sensitivity Analysis
Question: Although the focus of sensitivity analysis is typically on how changes in variables will affect profit (as shown in Figure 3.5 “Sensitivity Analysis for Snowboard Company”), accountants also use sensitivity analysis to determine the impact of changes in variables on the break-even point and target profit. How is sensitivity analysis used to evaluate the impact changes in variables will have on break-even and target profit points?
Answer: Let’s look at an example for Snowboard Company. Assume the company is able to charge $275 per unit, instead of $250 per unit. How many units must Snowboard Company sell to break even? The following calculation is based on the shortcut formula presented earlier in the chapter:
Q=(F + Target Profit) / (S − V) x Q=($50,000+$0)÷($275−$150) x Q=$50,000 / $125
Q=400 units
Thus if the sales price per unit increases from $250 to $275, the break-even point decreases from 500 units (calculated earlier) to 400 units, which is a decrease of 100 units.
How would this same increase in sales price change the required number of units sold to achieve a profit of $30,000? We apply the same shortcut formula:
Q=(F + Target Profit) / (S − V)Q=($50,000+$30,000) / ($275−$150) x Q=$80,000 / $125
Q=640 units
Thus if the sales price per unit increases from $250 to $275, the number of units sold to achieve a profit of $30,000 decreases from 800 units (calculated earlier) to 640 units, which is a decrease of 160 units.
Business in Action 3.2
Performing Sensitivity Analysis for a Brewpub
Three entrepreneurs in California were looking for investors and banks to finance a new brewpub. Brewpubs focus on two segments: food from the restaurant segment, and freshly brewed beer from the beer production segment. All parties involved in the process of raising money—potential investors and banks, as well as the three entrepreneurs (i.e., the owners)—wanted to know what the new business’s projected profits would be. After months of research, the owners created a financial model that provided this information. Projected profits were slightly more than $300,000 for the first year (from sales of $1.95 million) and were expected to increase in each of the next four years.
One of the owners asked, “What if our projected revenues are too high? What will happen to profits if sales are lower than we expect? After all, we will have debt of well over $1 million, and I don’t want anyone coming after my personal assets if the business doesn’t have the money to pay!” Although all three owners felt the financial model was reasonably accurate, they decided to find the break-even point and the resulting margin of safety.
Because a brewpub does not sell “units” of a specific product, the owners found the break-even point in sales dollars. The owners knew the contribution margin ratio and all fixed costs from the financial model. With this information, they were able to calculate the break-even point and margin of safety. The worried owner was relieved to discover that sales could drop over 35 percent from initial projections before the brewpub incurred an operating loss.
Key Takeaway
- Sensitivity analysis shows how the cost-volume-profit model will change with changes in any of its variables. Although the focus is typically on how changes in variables affect profit, accountants often analyze the impact on the break-even point and target profit as well.
Check Yourself
This problem is an extension of an earlier check yourself. Recall that International Printer Machines (IPM) builds three computer printer models: Inkjet, Laser, and Color Laser. Base case information for these three products is as follows:
| Inkjet | Laser | Color Laser | Total | |
| Selling price per unit | $250 | $400 | $1,600 | |
| Variable cost per unit | $100 | $150 | $ 800 | |
| Expected unit sales (annual) | 12,000 | 6,000 | 2,000 | 20,000 |
| Sales mix | 60 percent | 30 percent | 10 percent | 100 percent |
Total annual fixed costs are $5,000,000. Assume that each scenario that follows is independent of the others. Unless stated otherwise, the variables are the same as in the base case.
- Prepare a contribution margin income statement for the base case. Use the format shown in Figure 3.4 “Income Statement for Amy’s Accounting Service”.
- How will total profit change if the Laser sales price increases by 10 percent? (Hint:Compare your result with requirement 1.)
- How will total profit change if the Inkjet sales volume decreases by 4,000 units and the sales volume of other products remains the same?
- How will total profit change if fixed costs decrease by 20 percent?
Solution
Base Case:
-
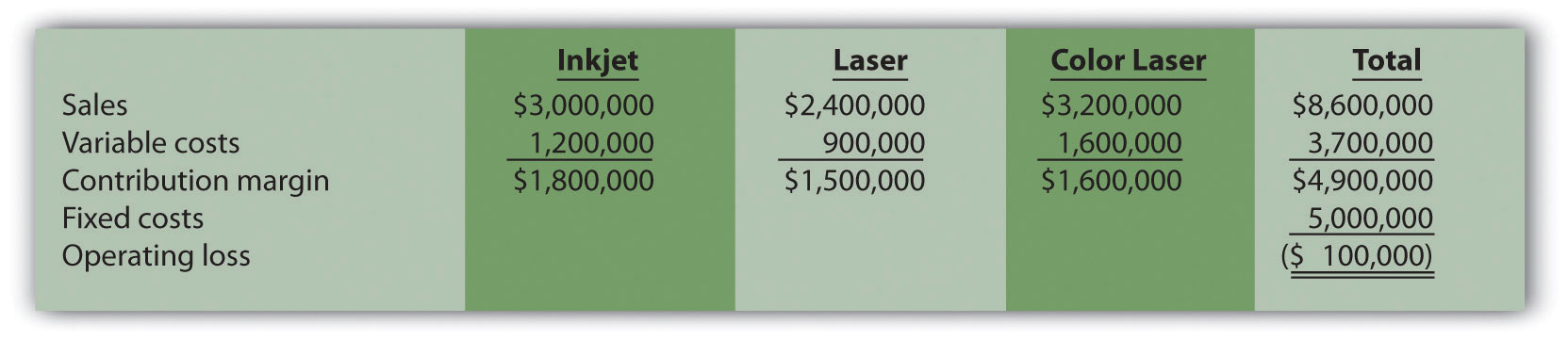
-
Laser sales price increases 10 percent:
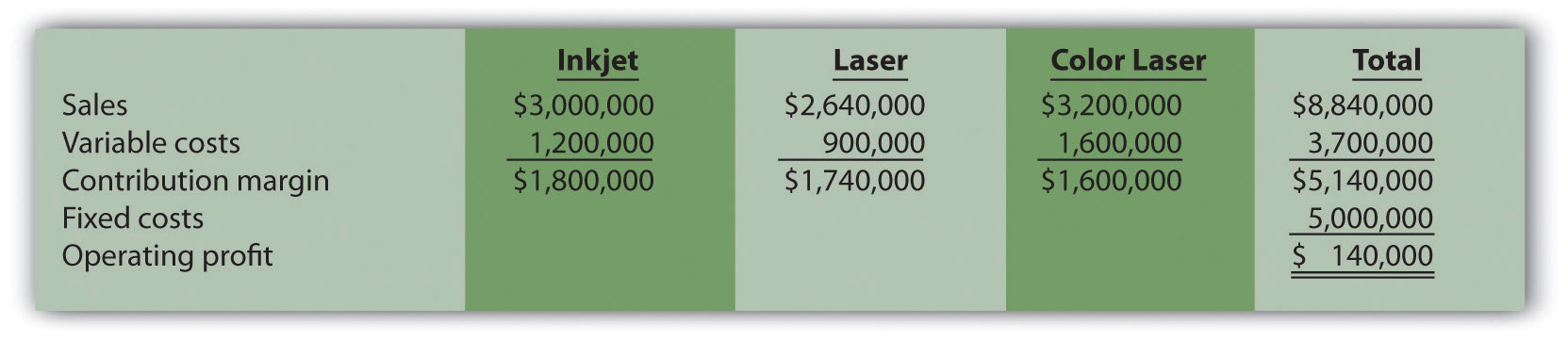
Total profit would increase $240,000 (from loss of $100,000 in base case to profit of $140,000 in this scenario).
-
Inkjet sales volume decreases 4,000 units:
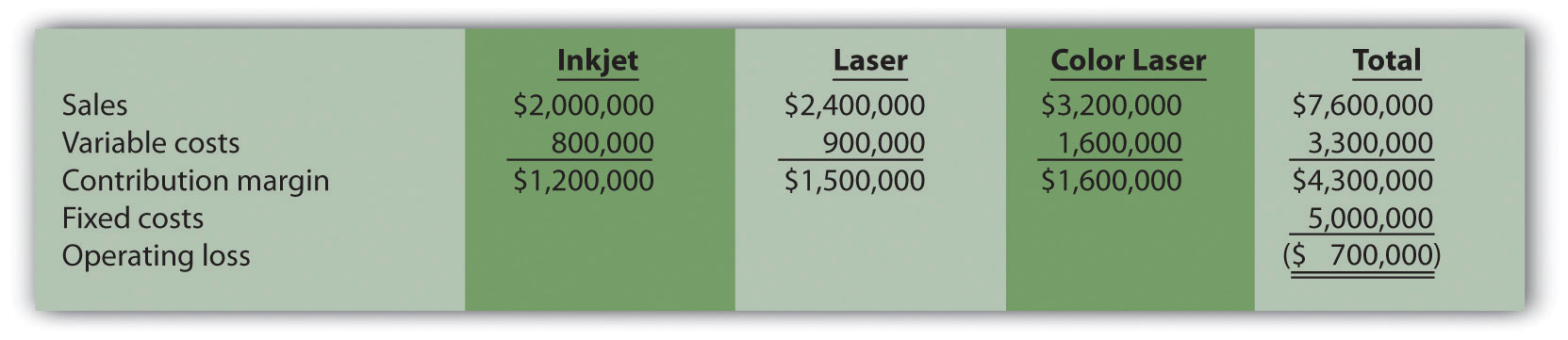
Total profit would decrease $600,000 (from loss of $100,000 in base case to loss of $700,000 in this scenario).
-
Fixed costs decrease 20 percent:
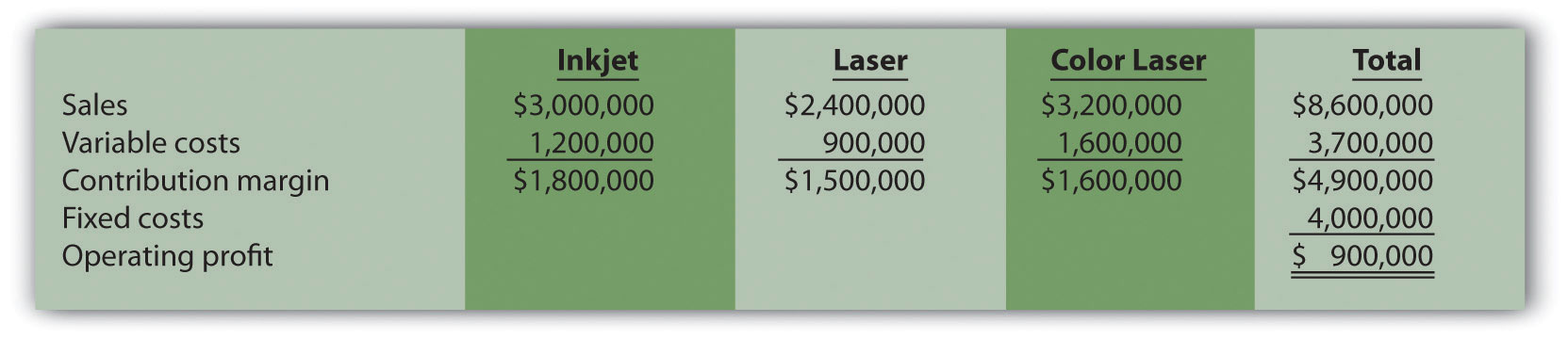
Total profit would increase $1,000,000 (from loss of $100,000 in base case to profit of $900,000 in this scenario).
3.4 Impact of Cost Structure on Cost-Volume-Profit Analysis
Learning Objectives
- Understand how cost structure affects cost-volume-profit sensitivity analysis.
Question: Describing an organization’s cost structure helps us to understand the amount of fixed and variable costs within the organization. What is meant by the term cost structure?
Answer: Cost structure is the term used to describe the proportion of fixed and variable costs to total costs. For example, if a company has $80,000 in fixed costs and $20,000 in variable costs, the cost structure is described as 80 percent fixed costs and 20 percent variable costs.
Question: Operating leverage refers to the level of fixed costs within an organization. How do we determine if a company has high operating leverage?
Answer: Companies with a relatively high proportion of fixed costs have high operating leverage. For example, companies that produce computer processors, such as NEC and Intel, tend to make large investments in production facilities and equipment and therefore have a cost structure with high fixed costs. Businesses that rely on direct labor and direct materials, such as auto repair shops, tend to have higher variable costs than fixed costs.
Operating leverage is an important concept because it affects how sensitive profits are to changes in sales volume. This is best illustrated by comparing two companies with identical sales and profits but with different cost structures, as we do in Figure 3.6 “Operating Leverage Example”. High Operating Leverage Company (HOLC) has relatively high fixed costs, and Low Operating Leverage Company (LOLC) has relatively low fixed costs.
Figure 3.6 Operating Leverage Example

One way to observe the importance of operating leverage is to compare the break-even point in sales dollars for each company. HOLC needs sales of $375,000 to break even (= $300,000 ÷ 0.80), whereas LOLC needs sales of $166,667 to break even (= $50,000 ÷ 0.30).
Question: Why don’t all companies strive for low operating leverage to lower the break-even point?
Answer: In Figure 3.6 “Operating Leverage Example”, LOLC looks better up to the sales point of $500,000 and profit of $100,000. However, once sales exceed $500,000, HOLC will have higher profit than LOLC. This is because every additional dollar in sales will provide $0.80 in profit for HOLC (80 percent contribution margin ratio), and only $0.30 in profit for LOLC (30 percent contribution margin ratio). If a company is relatively certain of increasing sales, then it makes sense to have higher operating leverage.
Financial advisers often say, “the higher the risk, the higher the potential profit,” which can also be stated as “the higher the risk, the higher the potential loss.” The same applies to operating leverage. Higher operating leverage can lead to higher profit. However, high operating leverage companies that encounter declining sales tend to feel the negative impact more than companies with low operating leverage.
To prove this point, let’s assume both companies in Figure 3.6″Operating Leverage Example” experience a 30 percent decrease in sales. HOLC’s profit would decrease by $120,000 (= 30 percent × $400,000 contribution margin) and LOLC’s profit would decrease by $45,000 (= 30 percent × $150,000 contribution margin). HOLC would certainly feel the pain more than LOLC.
Now assume both companies in Figure 3.6 “Operating Leverage Example” experience a 30 percent increase in sales. HOLC’s profit would increase by $120,000 (= 30 percent × $400,000 contribution margin) and LOLC’s profit would increase by $45,000 (= 30 percent × $150,000 contribution margin). HOLC benefits more from increased sales than LOLC.
Key Takeaways
- The cost structure of a firm describes the proportion of fixed and variable costs to total costs. Operating leverage refers to the level of fixed costs within an organization. The term “high operating leverage” is used to describe companies with relatively high fixed costs. Firms with high operating leverage tend to profit more from increasing sales, and lose more from decreasing sales than a similar firm with low operating leverage.
3.5 Using a Contribution Margin When Faced with Resource Constraints
Learning Objective
- Use an alternative form of contribution margin when faced with a resource constraint.
Question: Many companies have limited resources in such areas as labor hours, machine hours, facilities, and materials. These constraints will likely affect a company’s ability to produce goods or provide services. When a company that produces multiple products faces a constraint, managers often calculate the contribution margin per unit of constraint in addition to the contribution margin per unit. The contribution margin per unit of constraint is the contribution margin per unit divided by the units of constrained resource required to produce one unit of product. How is this measure used by managers to make decisions when faced with resource constraints?
Answer: Let’s examine the Kayaks-For-Fun example introduced earlier in the chapter. The company produces two kayak models, River and Sea. Based on the information shown, Kayaks-For-Fun would prefer to sell more of the River model because it has the highest contribution margin per unit.

Kayaks-For-Fun has a total of 320 labor hours available each month. The specialized skills required to build the kayaks makes it difficult for management to find additional workers. Assume the River model requires 4 labor hours per unit and the Sea model requires 1 labor hour per unit (most of the variable cost for the Sea model is related to expensive materials required for production). Kayaks-For-Fun sells everything it produces. Given its labor hours constraint, the company would prefer to maximize the contribution margin per labor hour.

Based on this information, Kayaks-For-Fun would prefer to sell the Sea model because it provides a contribution margin per labor hour of $150 versus $100 for the River model. The company would prefer only to make the Sea model, which would yield a total contribution margin of $48,000 (= $150 × 320 hours). If the River model were the only model produced, the total contribution margin to the company would be $32,000 (= $100 × 320 hours).
Analysis such as this often leads to further investigation. It may be that Kayaks-For-Fun can find additional labor to alleviate this resource constraint. Or perhaps the production process can be modified in a way that reduces the labor required to build the River model (e.g., through increased automation). Whatever the outcome, companies with limited resources are wise to calculate the contribution margin per unit of constrained resource.
Key Takeaway
- Many organizations operate with limited resources in areas such as labor hours, machine hours, facilities, or materials. The contribution margin per unit of constraint is a helpful measure in determining how constrained resources should be utilized.
Check Yourself
This knowledge check is based on the information for Kayaks-For-Fun presented previously. Assume Kayaks-For-Fun found additional labor, thereby eliminating this resource constraint. However, the company now faces limited available machine hours. It has a total of 3,000 machine hours available each month. The River model requires 16 machine hours per unit, and the Sea model requires 10 machine hours per unit.
- Calculate the contribution margin per unit of constrained resource for each model.
- Which model would Kayaks-For-Fun prefer to sell to maximize overall company profit?
Solution:
-

- Kayaks-For-Fun would prefer to sell the River model because it provides a contribution margin per machine hour of $25 compared to $15 for the Sea model. If only the River model were sold, the total contribution margin would be $75,000 (= $25 × 3,000 machine hours). If only the Sea model were sold, the total contribution margin would be $45,000 (= $15 × 3,000 machine hours).
3.6 Using Variable Costing to Make Decisions
Learning Objective
-
Understand how managers use variable costing to make decisions.
In Chapter 2, we discussed how to report manufacturing costs and nonmanufacturing costs following U.S. Generally Accepted Accounting Principles (U.S. GAAP). Under U.S. GAAP, all nonmanufacturing costs (selling and administrative costs) are treated as period costs because they are expensed on the income statement in the period in which they are incurred. All costs associated with production are treated as product costs, including direct materials, direct labor, and fixed and variable manufacturing overhead. These costs are attached to inventory as an asset on the balance sheet until the goods are sold, at which point the costs are transferred to cost of goods sold on the income statement as an expense. This method of accounting is called absorption costing because all manufacturing overhead costs (fixed and variable) are absorbed into inventory until the goods are sold. (The term full costing is also used to describe absorption costing.)
Question: Although absorption costing is used for external reporting, managers often prefer to use an alternative costing approach for internal reporting purposes called variable costing. What is variable costing, and how does it compare to absorption costing?
Answer: Variable costing requires that all variable production costs be included in inventory, and all fixed production costs (fixed manufacturing overhead) be reported as period costs. Thus all fixed production costs are expensed as incurred.
The only difference between absorption costing and variable costing is in the treatment of fixed manufacturing overhead. Using absorption costing, fixed manufacturing overhead is reported as a product cost. Using variable costing, fixed manufacturing overhead is reported as a period cost. Figure “Absorption Costing Versus Variable Costing” summarizes the similarities and differences between absorption costing and variable costing.
Figure 3.7 Absorption Costing Versus Variable Costing

Impact of Absorption Costing and Variable Costing on Profit
Question: If a company uses just-in-time inventory, and therefore has no beginning or ending inventory, profit will be exactly the same regardless of the costing approach used. However, most companies have units of product in inventory at the end of the reporting period. How does the use of absorption costing affect the value of ending inventory?
Answer: Since absorption costing includes fixed manufacturing overhead as a product cost, all products that remain in ending inventory (i.e., are unsold at the end of the period) include a portion of fixed manufacturing overhead costs as an asset on the balance sheet. Since variable costing treats fixed manufacturing overhead costs as period costs, all fixed manufacturing overhead costs are expensed on the income statement when incurred. Thus if the quantity of units produced exceeds the quantity of units sold, absorption costing will result in higher profit.
We illustrate this concept with an example. The following information is for Bullard Company, a producer of clock radios:

Assume Bullard has no finished goods inventory at the beginning of month 1. We will look at absorption costing versus variable costing for three different scenarios:
- Month 1 scenario: 10,000 units produced equals 10,000 units sold
- Month 2 scenario: 10,000 units produced is greater than 9,000 units sold
- Month 3 scenario: 10,000 units produced is less than 11,000 units sold
Month 1: Number of Units Produced Equals Number of Units Sold
Question: During month 1, Bullard Company sells all 10,000 units produced during the month. How does operating profit compare using absorption costing and variable costing when the number of units produced equals the number of units sold?
Answer: Figure 3.8 “Number of Units Produced Equals Number of Units Sold” presents the results for each costing method. Notice that the absorption costing income statement is called a traditional income statement, and the variable costing income statement is called a contribution margin income statement.
As you review Figure 3.8 “Number of Units Produced Equals Number of Units Sold”, notice that when the number of units produced equals the number sold, profit totaling $90,000 is identical for both costing methods. With absorption costing, fixed manufacturing overhead costs are fully expensed because all units produced are sold (there is no ending inventory). With variable costing, fixed manufacturing overhead costs are treated as period costs and therefore are always expensed in the period incurred. Because all other costs are treated the same regardless of the costing method used, profit is identical when the number of units produced and sold is the same.
Figure 3.8 Number of Units Produced Equals Number of Units Sold
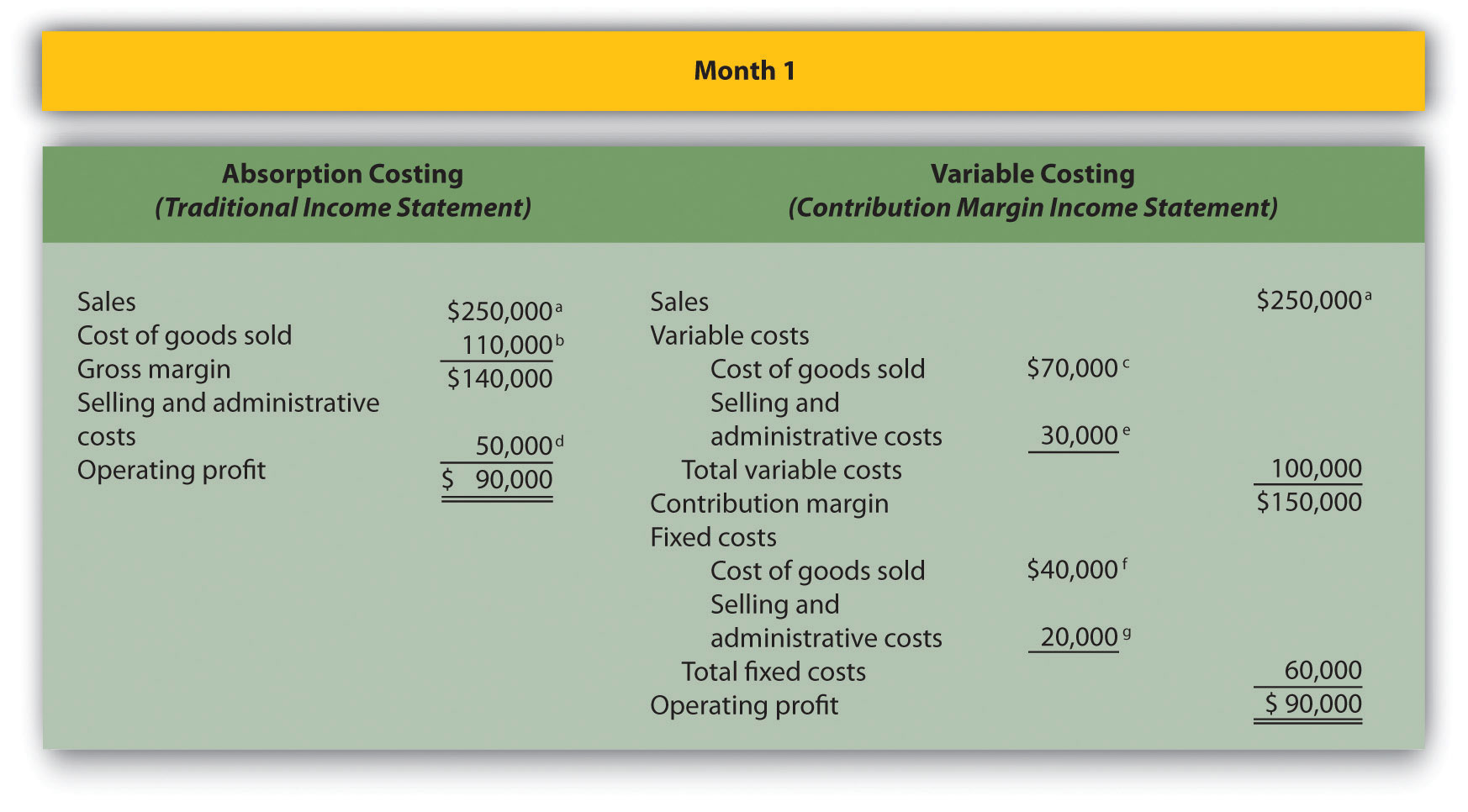
a $250,000 = $25 × 10,000 units sold.
b $110,000 = ($4 per unit fixed production cost × 10,000 units sold) + ($7 per unit variable production cost × 10,000 units sold).
c $70,000 = $7 per unit variable production cost × 10,000 units sold.
d $50,000 = $20,000 fixed selling and admin. cost + ($3 per unit variable selling and admin. cost × 10,000 units sold).
e $30,000 = $3 per unit variable selling and admin. cost × 10,000 units sold.
f Variable costing treats fixed manufacturing overhead as a period cost. Thus all fixed manufacturing overhead costs are expensed in the period incurred regardless of the level of sales.
g Given.
Month 2: Number of Units Produced Is Greater Than Number of Units Sold
Question: During month 2, Bullard Company produces 10,000 units but sells only 9,000 units. How does operating profit compare using absorption costing and variable costing when the number of units produced is greater than the number of units sold?
Answer: Figure 3.9 “Number of Units Produced Is Greater Than Number of Units Sold” presents the results for each costing method. Notice that absorption costing results in higher profit. When absorption costing is used, a portion of fixed manufacturing overhead costs remains in ending inventory as an asset on the balance sheet until the goods are sold. However, variable costing requires that all fixed manufacturing overhead costs be expensed as incurred regardless of the level of sales. Thus when more units are produced than are sold, variable costing results in higher costs and lower profit.
The difference in profit between the two methods of $4,000 (= $79,000 − $75,000) is attributed to the $4 per unit fixed manufacturing overhead cost assigned to the 1,000 units in ending inventory using absorption costing ($4,000 = $4 × 1,000 units).
Figure 3.9 Number of Units Produced Is Greater Than Number of Units Sold
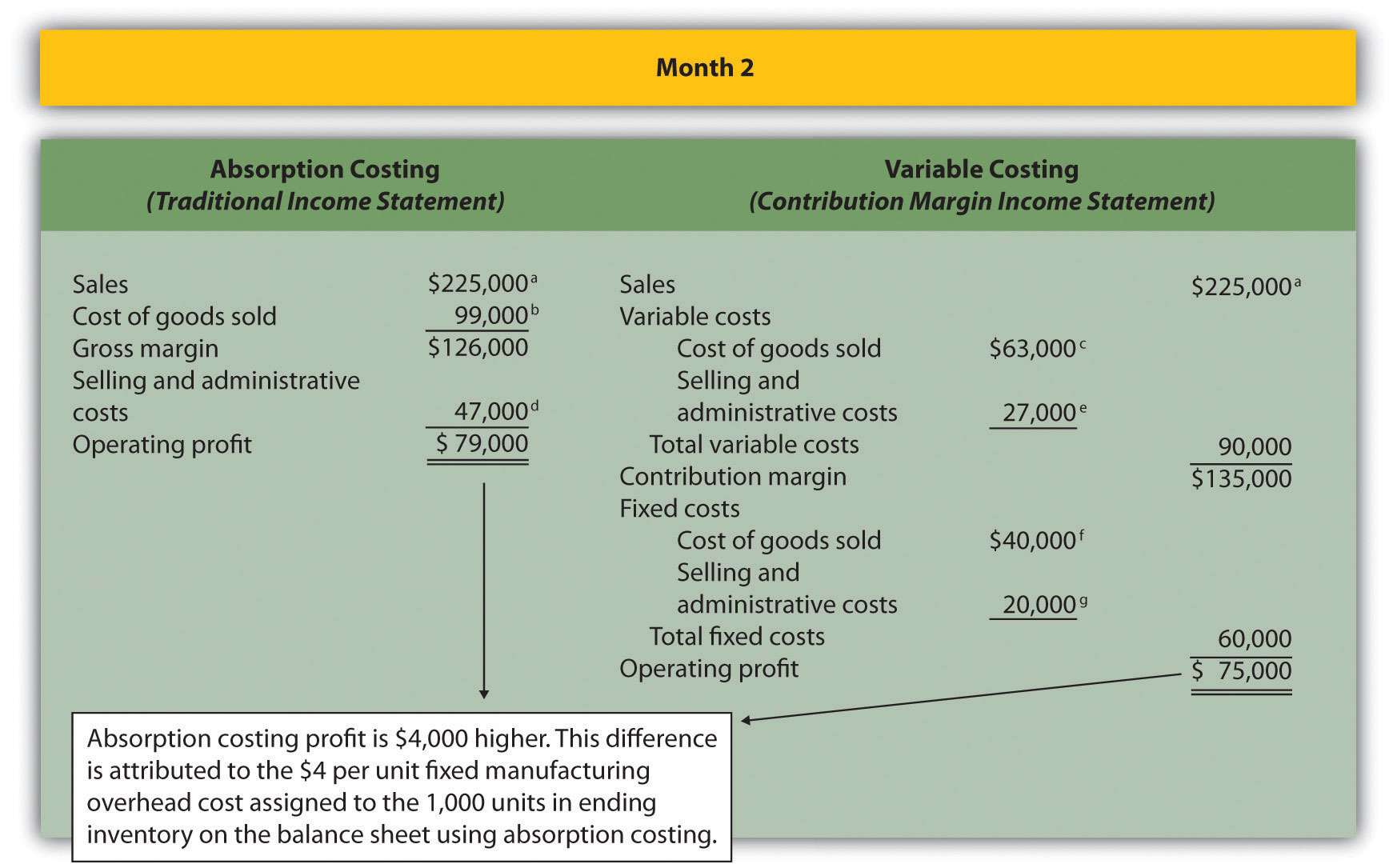
a $225,000 = $25 × 9,000 units sold.
b $99,000 = ($4 per unit fixed production cost × 9,000 units sold) + ($7 per unit variable production cost × 9,000 units sold).
c $63,000 = $7 per unit variable production cost × 9,000 units sold.
d $47,000 = $20,000 fixed selling and admin. cost + ($3 per unit variable selling and admin. cost × 9,000 units sold).
e $27,000 = $3 per unit variable selling and admin. cost × 9,000 units sold.
f Variable costing always treats fixed manufacturing overhead as a period cost. Thus all fixed manufacturing overhead costs are expensed in the period incurred regardless of the level of sales.
g Given.
Month 3: Number of Units Produced Is Less Than Number of Units Sold
Question: During month 3, Bullard Company produces 10,000 units but sells 11,000 units (1,000 units were left over from month 2 and therefore were in inventory at the beginning of month 3). How does operating profit compare using absorption costing and variable costing when the number of units produced is less than the number of units sold?
Answer: Figure 3.10 “Number of Units Produced Is Less Than Number of Units Sold” presents the results for each costing method. Using variable costing, the $40,000 in fixed manufacturing overhead costs continues to be expensed when incurred. However, using absorption costing, the entire $40,000 is expensed because all 10,000 units produced were sold; an additional $4,000 related to the 1,000 units produced last month and pulled from inventory this month is also expensed. Thus when fewer units are produced than are sold, absorption costing results in higher costs and lower profit.
The difference in profit between the two methods of $4,000 (= $105,000 − $101,000) is attributed to the $4 per unit fixed manufacturing overhead cost assigned to the 1,000 units in inventory on the balance sheet at the end of month 2 and recorded as cost of goods sold during month 3 using absorption costing ($4,000 = $4 × 1,000 units).
Figure 3.10 Number of Units Produced Is Less Than Number of Units Sold
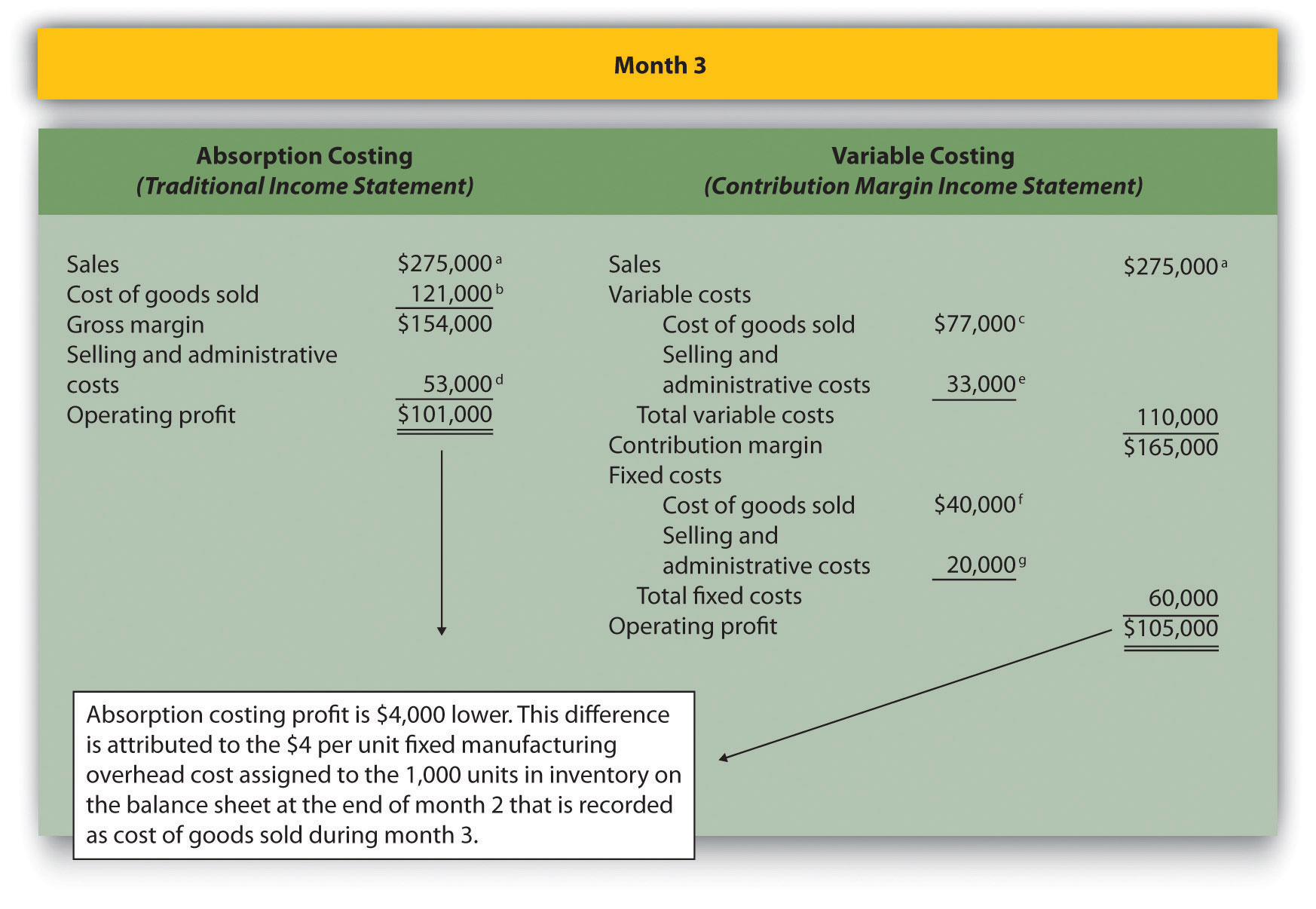
a $275,000 = $25 × 11,000 units sold.
b $121,000 = ($4 per unit fixed production cost × 11,000 units sold) + ($7 per unit variable production cost × 11,000 units sold).
c $77,000 = $7 per unit variable production cost × 11,000 units sold.
d $53,000 = $20,000 fixed selling and admin. cost + ($3 per unit variable selling and admin. cost × 11,000 units sold).
e $33,000 = $3 per unit variable selling and admin. cost × 11,000 units sold.
f Variable costing always treats fixed manufacturing overhead as a period cost. Thus all fixed manufacturing overhead costs are expensed in the period incurred regardless of the level of sales.
g Given.
Advantages of Using Variable Costing
Question: Why do organizations use variable costing?
Answer: Variable costing provides managers with the information necessary to prepare a contribution margin income statement, which leads to more effective cost-volume-profit (CVP) analysis. By separating variable and fixed costs, managers are able to determine contribution margin ratios, break-even points, and target profit points, and to perform sensitivity analysis. Conversely, absorption costing meets the requirements of U.S. GAAP, but is not as useful for internal decision-making purposes.
Another advantage of using variable costing internally is that it prevents managers from increasing production solely for the purpose of inflating profit. For example, assume the manager at Bullard Company will receive a bonus for reaching a certain profit target but expects to be $15,000 short of the target. The company uses absorption costing, and the manager realizes increasing production (and therefore increasing inventory levels) will increase profit. The manager decides to produce 20,000 units in month 4, even though only 10,000 units will be sold. Half of the $40,000 in fixed production cost ($20,000) will be included in inventory at the end of the period, thereby lowering expenses on the income statement and increasing profit by $20,000. At some point, this will catch up to the manager because the company will have excess or obsolete inventory in future months. However, in the short run, the manager will increase profit by increasing production. This strategy does not work with variable costing because all fixed manufacturing overhead costs are expensed as incurred, regardless of the level of sales.
Key Takeaways
-
The only difference between absorption costing and variable costing is in the treatment of fixed manufacturing overhead costs. Absorption costing treats fixed manufacturing overhead as a product cost (included in inventory on the balance sheet until sold), while variable costing treats fixed manufacturing overhead as a period cost (expensed on the income statement as incurred).
When comparing absorption costing with variable costing, the following three rules apply: (1) When units produced equals units sold, profit is the same for both costing approaches. (2) When units produced is greater than units sold, absorption costing yields the highest profit. (3) When units produced is less than units sold, variable costing yields the highest profit.
Check Yourself
Winter Sports, Inc., produces snowboards. The company has no finished goods inventory at the beginning of year 1. The following information pertains to Winter Sports, Inc.,:

-
All 100,000 units produced during year 1 are sold during year 1.
- Prepare a traditional income statement assuming the company uses absorption costing.
- Prepare a contribution margin income statement assuming the company uses variable costing.
-
Although 100,000 units are produced during year 2, only 80,000 are sold during the year. The remaining 20,000 units are in finished goods inventory at the end of year 2.
- Prepare a traditional income statement assuming the company uses absorption costing.
- Prepare a contribution margin income statement assuming the company uses variable costing.
Solution
-
-
Traditional income statement (absorption costing), year 1:

a $20,000,000 = $200 × 100,000 units sold.
b $13,500,000 = ($5 per unit fixed production cost × 100,000 units sold) + ($130 per unit variable production cost × 100,000 units sold).
c $1,800,000 = $800,000 fixed selling and admin. cost + ($10 per unit variable selling and admin. cost × 100,000 units sold).
-
Contribution margin income statement (variable costing), year 1:

a $20,000,000 = $200 × 100,000 units sold.
b $13,000,000 = $130 per unit variable production cost × 100,000 units sold.
c $1,000,000 = $10 per unit variable selling and admin. cost × 100,000 units sold.
d Variable costing treats fixed manufacturing overhead as a period cost. Thus all fixed manufacturing overhead costs are expensed in the period incurred regardless of the level of sales.
e Given.
-
Traditional income statement (absorption costing), year 2:

a $16,000,000 = $200 × 80,000 units sold.
b $10,800,000 = ($5 per unit fixed production cost × 80,000 units sold) + ($130 per unit variable production cost × 80,000 units sold).
-
Contribution margin income statement (variable costing), year 2:

a $16,000,000 = $200 × 80,000 units sold.
b $10,400,000 = $130 per unit variable production cost × 80,000 units sold.
c $800,000 = $10 per unit variable selling and admin. cost × 80,000 units sold.
d Variable costing treats fixed manufacturing overhead as a period cost. Thus all fixed manufacturing overhead costs are expensed in the period incurred regardless of the level of sales.
e Given.
-
End-of-Chapter Exercises
Questions
- Describe the components of the profit equation.
- What is the difference between a variable cost and a fixed cost? Provide examples of each.
- You are asked to find the break-even point in units and in sales dollars. What does this mean?
- You are asked to find the target profit in units and in sales dollars. What does this mean?
- For a company with one product, describe the equation used to calculate the break-even point or target profit in (a) units, and (b) sales dollars.
- Distinguish between contribution margin per unit and contribution margin ratio.
- What does the term margin of safety mean? How might management use this information?
- How does the break-even point equation change for a company with multiple products or services compared to a single-product company?
- Describe the assumptions made to simplify the cost-volume-profit analysis described in the chapter.
- What is sensitivity analysis and how might it help those performing cost-volume-profit analysis?
- If you are asked to review the cost structure of an organization, what are you being asked to do?
- When might the contribution margin per unit of constraint be more effective than the contribution margin per unit for making decisions?
- Describe the difference between absorption costing and variable costing.
- Why do some organizations use variable costing?
Brief Exercises
15. Planning at Snowboard Company. Refer to the dialogue at Snowboard Company presented at the beginning of the chapter. What information is Recilia, vice president of sales, requesting from Lisa, the company accountant? How does Recilia plan on using this information?
16. Contribution Margin Calculations. Ace Company sells lawn mowers for $200 per unit. Variable cost per unit is $40, and fixed costs total $4,000. Find (a) the contribution margin per unit, and (b) the contribution margin ratio.
17. Weighted Average Contribution Margin Calculation. Radio Control, Inc., sells radio controlled cars for $300 per unit representing 80 percent of total sales, and radio controlled boats for $400 per unit representing 20 percent of total sales. Variable cost per unit is $150 for cars and $300 for boats. Find (a) the contribution margin per unit for each product, and (b) the weighted average contribution margin per unit.
18. Sensitivity Analysis, Sales Price. Refer to the base case for Snowboard Company presented in the first column of Figure 3.5 “Sensitivity Analysis for Snowboard Company”. Assume the unit sales price decreases by 10 percent. Calculate (a) the new projected profit, (b) the dollar change in profit from the base case, and (c) the percent change in profit from the base case.
19. Sensitivity Analysis, Unit Sales. Refer to the base case for Snowboard Company presented in the first column of Figure 3.5 “Sensitivity Analysis for Snowboard Company”. Assume the number of units sold increases by 10 percent. Calculate (a) the new projected profit, (b) the dollar change in profit from the base case, and (c) the percent change in profit from the base case.
20. Operating Leverage. High operating leverage means:
- The company has relatively low fixed costs.
- The company has relatively high fixed costs.
- The company will have to sell more units than a comparable company with low operating leverage to break even.
- The company will have to sell fewer units than a comparable company with low operating leverage to break even.
- Both (2) and (3) are correct.
- Both (1) and (4) are correct.
21. Contribution Margin per Unit of Constraint. Paint Toys Company sells paint ball guns for $100 per unit. Variable cost is $60 per unit. Each paint ball gun requires 1.25 machine hours and 2.00 direct labor hours to produce. Calculate the contribution margin (a) per unit, (b) per machine hour, and (c) per direct labor hour.
22. Absorption Costing Versus Variable Costing. Describe the difference between absorption costing and variable costing. Which approach yields the highest profit when the units produced are greater than the units sold? Explain.
Exercises:
23. Break-Even Point and Target Profit Measured in Units (Single Product). Nellie Company has monthly fixed costs totaling $100,000 and variable costs of $20 per unit. Each unit of product is sold for $25.
Required:
-
- Calculate the contribution margin per unit.
- Find the break-even point in units.
- How many units must be sold to earn a monthly profit of $40,000? 24 . Break-Even Point and Target Profit Measured in Sales Dollars (Single Product). Nellie Company has monthly fixed costs totaling $100,000 and variable costs of $20 per unit. Each unit of product is sold for $25 (these data are the same as the previous exercise):
Required:
1. Calculate the contribution margin ratio.
2. Find the break-even point in sales dollars.
3. What amount of sales dollars is required to earn a monthly profit of $60,000?
25. Margin of Safety (Single Product). Nellie Company has monthly fixed costs totaling $100,000 and variable costs of $20 per unit. Each unit of product is sold for $25 (these data are the same as the previous exercise). Assume Nellie Company expects to sell 24,000 units of product this coming month.
Required:
- Find the margin of safety in units.
- Find the margin of safety in sales dollars.
26. Break-Even Point and Target Profit Measured in Units (Multiple Products). Hi-Tech Incorporated produces two different products with the following monthly data.
| Cell | GPS | Total | |
| Selling price per unit | $100 | $400 | |
| Variable cost per unit | $ 40 | $240 | |
| Expected unit sales | 21,000 | 9,000 | 30,000 |
| Sales mix | 70 percent | 30 percent | 100 percent |
| Fixed costs | $1,800,000 |
Assume the sales mix remains the same at all levels of sales.
Required:
- Calculate the weighted average contribution margin per unit.
- How many units in total must be sold to break even?
- How many units of each product must be sold to break even?
- How many units in total must be sold to earn a monthly profit of $180,000?
- How many units of each product must be sold to earn a monthly profit of $180,000?
27. Break-Even Point and Target Profit Measured in Sales Dollars (Multiple Products). Hi-Tech Incorporated produces two different products with the following monthly data (these data are the same as the previous exercise).
| Cell | GPS | Total | |
| Selling price per unit | $100 | $400 | |
| Variable cost per unit | $ 40 | $240 | |
| Expected unit sales | 21,000 | 9,000 | 30,000 |
| Sales mix | 70 percent | 30 percent | 100 percent |
| Fixed costs | $1,800,000 |
Assume the sales mix remains the same at all levels of sales.
Required:
Round your answers to the nearest hundredth of a percent and nearest dollar where appropriate. (An example for percentage calculations is 0.434532 = 0.4345 = 43.45 percent; an example for dollar calculations is $378.9787 = $379.)
- Using the information provided, prepare a contribution margin income statement for the month similar to the one in Figure 3.4 “Income Statement for Amy’s Accounting Service”.
- Calculate the weighted average contribution margin ratio.
- Find the break-even point in sales dollars.
- What amount of sales dollars is required to earn a monthly profit of $540,000?
- Assume the contribution margin income statement prepared in requirement a is the company’s base case. What is the margin of safety in sales dollars?
28. Changes in Sales Mix. Hi-Tech Incorporated produces two different products with the following monthly data (these data are the same as the previous exercise).
| Cell | GPS | Total | |
| Selling price per unit | $100 | $400 | |
| Variable cost per unit | $ 40 | $240 | |
| Expected unit sales | 21,000 | 9,000 | 30,000 |
| Sales mix | 70 percent | 30 percent | 100 percent |
| Fixed costs | $1,800,000 |
Required:
- If the sales mix shifts to 50 percent Cell and 50 percent GPS, would the break-even point in units increase or decrease? Explain. (Detailed calculations are not necessary but may be helpful in confirming your answer.)
- Go back to the original projected sales mix. If the sales mix shifts to 80 percent Cell and 20 percent GPS, would the break-even point in units increase or decrease? Explain. (Detailed calculations are not necessary but may be helpful in confirming your answer.)
28. CVP Sensitivity Analysis (Single Product). Bridgeport Company has monthly fixed costs totaling $200,000 and variable costs of $40 per unit. Each unit of product is sold for $50. Bridgeport expects to sell 30,000 units each month (this is the base case).
Required:
For each of the independent situations in requirements 2 through 4, assume that the number of units sold remains at 30,000.
- Prepare a contribution margin income statement for the base case.
- Refer to the base case. What would the operating profit be if the unit sales price increases 10 percent?
- Refer to the base case. What would the operating profit be if the unit variable cost decreases 20 percent?
- Refer to the base case. What would the operating profit be if total fixed costs decrease 20 percent?
29. CVP Sensitivity Analysis (Multiple Products). Gonzalez Company produces two different products that have the following monthly data (this is the base case).
| Cruiser | Racer | Total | |
| Selling price per unit | $300 | $1,200 | |
| Variable cost per unit | $120 | $ 720 | |
| Expected unit sales | 1,400 | 600 | 2,000 |
| Sales mix | 70 percent | 30 percent | 100 percent |
| Fixed costs | $180,000 |
Required:
For each of the independent situations in requirements 2 through 4, assume that total sales remains at 2,000 units.
- Prepare a contribution margin income statement.
- Refer to the base case. What would the operating profit be if the Cruiser sales price (1) increases 20 percent, or (2) decreases 20 percent?
- Refer to the base case. What would the operating profit be if the Cruiser sales volume increases 400 units with a corresponding decrease of 400 units in Racer sales?
- Refer to the base case. What would the operating profit be if total fixed costs increase five percent? Does this increase in fixed costs result in higher operating leverage or lower operating leverage? Explain.
30. Contribution Margin with Resource Constraints. CyclePath Company produces two different products that have the following price and cost characteristics.
| Bicycle | Tricycle | |
| Selling price per unit | $200 | $100 |
| Variable cost per unit | $120 | $ 50 |
Management believes that pushing sales of the Bicycle product would maximize company profits because of the high contribution margin per unit for this product. However, only 50,000 labor hours are available each year, and the Bicycle product requires 4 labor hours per unit while the Tricycle model requires 2 labor hours per unit. The company sells everything it produces.
Required:
- Calculate the contribution margin per unit of constrained resource for each model.
- Which model would CyclePath prefer to sell to maximize overall company profit? Explain.
31. Absorption Costing Versus Variable Costing. Technic Company produces portable CD players. The company has no finished goods inventory at the beginning of year 1. The following information pertains to Technic Company.

Required:
-
All 50,000 units produced during year 1 are sold during year 1.
- Prepare a traditional income statement assuming the company uses absorption costing.
- Prepare a contribution margin income statement assuming the company uses variable costing.
-
Although 50,000 units are produced during year 2, only 40,000 are sold during the year. The remaining 10,000 units are in finished goods inventory at the end of year 2.
- Prepare a traditional income statement assuming the company uses absorption costing.
- Prepare a contribution margin income statement assuming the company uses variable costing.
-
Problems
32. CVP and Sensitivity Analysis (Single Product). Madera Company has annual fixed costs totaling $120,000 and variable costs of $3 per unit. Each unit of product is sold for $15. Madera expects to sell 12,000 units this year (this is the base case).
Required:
-
- Find the break-even point in units.
- How many units must be sold to earn an annual profit of $50,000? (Round to the nearest unit.)
- Find the break-even point in sales dollars.
- What amount of sales dollars is required to earn an annual profit of $70,000?
- Find the margin of safety in units and in sales dollars.
- Prepare a contribution margin income statement for the base case.
- What will the operating profit (loss) be if the sales price decreases 30 percent? (Assume total sales remains at 12,000 units, and round to the nearest cent where appropriate.)
- Go back to the base case. What will the operating profit (loss) be if the variable cost per unit increases 10 percent? (Assume total sales remains at 12,000 units, and round to the nearest cent where appropriate.)
33. CVP Analysis and Cost Structure (Single Product).Riviera Incorporated produces flat panel televisions. The company has annual fixed costs totaling $10,000,000 and variable costs of $600 per unit. Each unit of product is sold for $1,000. Riviera expects to sell 70,000 units this year.
Required:
-
-
-
-
- Find the break-even point in units.
- How many units must be sold to earn an annual profit of $2,000,000?
- Find the break-even point in sales dollars.
- What amount of sales dollars is required to earn an annual profit of $500,000?
- Find the margin of safety in units.
- Find the margin of safety in sales dollars.
- How much will operating profit change if fixed costs are 15 percent higher than anticipated? Would this increase in fixed costs result in higher or lower operating leverage? Explain.
-
-
-
34. CVP Analysis and Sales Mix (Multiple Products). Sierra Books Incorporated produces two different products with the following monthly data (this is the base case).
-
Text Lecture Notes Total Selling price per unit $100 $12 Variable cost per unit $ 60 $ 3 Expected unit sales 21,000 14,000 35,000 Sales mix 60 percent 40 percent 100 percent Fixed costs $750,000 Assume the sales mix remains the same at all levels of sales except for requirement i.
Required:
Round to the nearest unit of product, hundredth of a percent, and nearest cent where appropriate. (An example for unit calculations is 3,231.15 = 3,231; an example for percentage calculations is 0.434532 = 0.4345 = 43.45 percent; an example for dollar calculations is $378.9787 = $378.98.)
- Calculate the weighted average contribution margin per unit.
- How many units in total must be sold to break even?
- How many units of each product must be sold to break even?
- How many units in total must be sold to earn a monthly profit of $100,000?
- How many units of each product must be sold to earn a monthly profit of $100,000?
- Using the base case information, prepare a contribution margin income statement for the month
- Calculate the weighted average contribution margin ratio.
- Find the break-even point in sales dollars.
- What amount of sales dollars is required to earn a monthly profit of $80,000?
- Assume the contribution margin income statement prepared in requirement d is the company’s base case. What is the margin of safety in sales dollars?
- If the sales mix shifts more toward the Text product than the Lecture Notes product, would the break-even point in units increase or decrease? Explain. (Detail calculations are not necessary, but may be helpful in confirming your answer.)
- Calculate the weighted average contribution margin per unit.
35. CVP Analysis and Cost Structure (Service Company). Conway Electrical Services provides services to two types of clients: residential and commercial. The company’s contribution margin income statement for the year is shown (this is the base case). Fixed costs are known in total, but Conway does not allocate fixed costs to each department.

Required:
- Find the break-even point in sales dollars.
- What is the margin of safety in sales dollars?
- What amount of sales dollars is required to earn an annual profit of $750,000?
- Refer to the base case shown previously. What would the operating profit be if the Commercial variable costs are 20 percent higher than originally anticipated? How does this increase in Commercial variable costs impact the operating leverage of the company?
36. CVP and Sensitivity Analysis, Resource Constraint (Multiple Products). Hobby Shop Incorporated produces three different models with the following annual data (this is the base case).
| Plane | Car | Boat | Total | |
| Selling price per unit | $20 | $14 | $24 | |
| Variable cost per unit | $ 5 | $ 7 | $ 8 | |
| Expected unit sales | 30,000 | 50,000 | 20,000 | 100,000 |
| Sales mix | 30 percent | 50 percent | 20 percent | 100 percent |
| Fixed costs | $650,000 |
Assume the sales mix remains the same at all levels of sales except for requirements i and j.
Required:
Round to the nearest unit of product, hundredth of a percent, and nearest cent where appropriate. (An example for unit calculations is 3,231.151 = 3,231; an example for percentage calculations is 0.434532 = 0.4345 = 43.45 percent; an example for dollar calculations is $378.9787 = $378.98.)
- Calculate the weighted average contribution margin per unit.
- How many units in total must be sold to break even?
- How many units of each product must be sold to break even?
- How many units in total must be sold to earn an annual profit of $500,000?
- How many units of each product must be sold to earn an annual profit of $500,000?
- Using the base case information, prepare a contribution margin income statement for the year
- Calculate the weighted average contribution margin ratio.
- Find the break-even point in sales dollars.
- What amount of sales dollars is required to earn an annual profit of $400,000?
- Go back to the base case contribution margin income statement prepared in requirement d. What would the operating profit be if the Plane sales price (1) increases 10 percent, or (2) decreases 10 percent? (Assume total sales remains at 100,000 units.)
- Go back to the base case contribution margin income statement prepared in requirement d. If the sales mix shifts more toward the Car product than to the other two products, would the break-even point in units increase or decrease? (Detailed calculations are not necessary.) Explain.
- Assume the company has a limited number of labor hours available in production, and management would like to make efficient use of these labor hours. The Plane product requires 4 labor hours per unit, the Car product requires 3 labor hours per unit, and the Boat product requires 5 hours per unit. The company sells everything it produces. Based on this information, calculate the contribution margin per labor hour for each model (round to the nearest cent), and determine the top two models the company would prefer to sell to maximize overall company profit.
37. Absorption Costing Versus Variable Costing. Wall Tech Company produces wood siding. The company has no finished goods inventory at the beginning of year 1. The following information pertains to Wall Tech Company.

Required:
-
All 200,000 units produced during year 1 are sold during year 1.
- Prepare a traditional income statement assuming the company uses absorption costing.
- Prepare a contribution margin income statement assuming the company uses variable costing.
-
Although 200,000 units are produced during year 2, only 170,000 units are sold during the year. The remaining 30,000 units are in finished goods inventory at the end of year 2.
- Prepare a traditional income statement assuming the company uses absorption costing.
- Prepare a contribution margin income statement assuming the company uses variable costing.
-
Although 200,000 units are produced during year 3, a total of 230,000 units are sold during the year. The 30,000 units remaining in inventory at the end of year 2 are sold during year 3.
- Prepare a traditional income statement assuming the company uses absorption costing.
- Prepare a contribution margin income statement assuming the company uses variable costing.
- Analyze the results in years 1 through 3 (requirements a through c).
One Step Further: Skill-Building Cases
38. Internet Project: CVP Analysis. Using the Internet, go to the Web site for Nordstrom, Inc.https://investor.nordstrom.com/financial-information/annual-reports . Find the most recent annual report and print the income statement (called the consolidated statements of earnings).
Required:
- Calculate the gross profit percentage (also called the gross margin percentage) by dividing the gross profit by net sales.
- Explain how the gross profit percentage is different than the contribution margin ratio (no calculations are necessary)?
39. Decision Making: Automated Versus Labor Intensive Production. Wood Furniture, Inc., builds high-quality wood desks. Management of the company is considering going from a labor-intensive process of building desks to an automated process that requires expensive machinery and equipment. If the company moves to an automated process, variable production costs will decrease (direct materials, direct labor, and variable manufacturing overhead) due to improved efficiency, and fixed production costs will increase as a result of additional depreciation costs. The costs predicted for the coming year are shown. The selling price is expected to be $900 per unit for both processes.
| Labor-Intensive Process | Automated Process | |
| Variable cost of goods sold | $490 per unit | $290 per unit |
| Fixed cost of goods sold (annual) | $1,000,000 | $2,600,000 |
| Variable selling and administrative | $10 per unit | $10 per unit |
| Fixed selling and admin. (annual) | $400,000 | $400,000 |
Required:
- Calculate the break-even point in units assuming that (1) the labor-intensive process is used, and (2) the automated process is used.
- Explain why there is such a significant difference in break-even points between the labor-intensive process and the automated process.
- Assume Wood Furniture, Inc., expects to produce and sell 8,000 units this coming year and is certain sales will grow by at least 10 percent per year in future years. Calculate the expected operating profit assuming that (1) the labor intensive process is used, and (2) the automated process is used.
- Using requirement c as a guide, explain whether management should stay with the labor-intensive process or switch to an automated process.
40. Group Activity: Sensitivity Analysis and Decision Making. Performance Sports produces inflatable rafts used for river rafting. Sales have grown slowly over the years, and cost increases are causing Performance Sports to incur losses. Financial data for the most recent year are shown.

Members of the management group at Performance Sports arrived at these three possible courses of action to return the company to profitability (each scenario is independent of the others):
Required:
Form groups of two to four students and assign one of the three options listed previously to each group. Each group must perform the following requirements:
- Increase the sales price for each raft by 10 percent, which will cause a 5 percent drop in sales volume. Although sales volume will drop 5 percent, the group believes the increased sales price will more than offset the drop in rafts sold.
- Decrease the sales price for each raft by 10 percent, which will cause an 8 percent increase in sales volume. Although the sales price will drop by 10 percent, the group believes an increase in rafts sold will more than offset the sales price reduction.
- Increase advertising costs by $200,000, which will increase sales volume by 15 percent. Although fixed selling and administrative costs will increase by $200,000, the group believes the increase in rafts sold will more than offset the increase in advertising costs.
- Calculate the projected operating profit (loss) for the option assigned, and determine whether the option is acceptable.
- Discuss and document the advantages and disadvantages of the option assigned.
- As a class, discuss each option based on the findings of your group.
41. Sensitivity Analysis Using Excel. Refer to the information for Performance Sports in Skill-Building Case 60. Prepare an Excel spreadsheet to calculate the operating profit (loss) for the base case and for each of the three scenarios presented in the case. Using the spreadsheet in the Computer Application box in this chapter as a guide, include “data entry” and “sensitivity analysis results” sections, and combine variable cost of goods sold and selling and administrative costs on one line and fixed cost of goods sold and selling and administrative costs on another line.
42. Ethics: Increasing Production to Boost Profit. Hauser Company produces heavy machinery used for snow removal. Over half of the production costs incurred by Hauser are related to fixed manufacturing overhead. Although the company has maximum production capacity of 20,000 units per year, only 2,000 units were produced and sold during year 1, yielding $25 million in operating losses. As required by U.S. GAAP, the company uses absorption costing.
At the beginning of year 2, the board of directors fired the president of the company and began searching for a new president who was willing to make substantial changes to get the company turned around. One candidate, Paul Glezner, indicated he could turn the company around within a year. He felt the company was producing too few products, and could benefit from increased production. The members of the board of directors were impressed and considered Paul’s contract demands: $10,000 in base annual salary, plus 30 percent of operating profit. Paul made it clear he would help the company for year 2, but intended to move on after the year ended.
Management of Hauser Company approached you with Paul’s offer and asked you to determine whether the offer is reasonable.
Required:
- Assume the company’s sales will remain close to 2,000 units in year 2. How does Paul intend to “turn the company around” during year 2?
- Why do you think Paul insists on leaving the company after year 2?
- What type of costing system would you recommend Hauser Company use during year 2? Explain.
Comprehensive Case
43. CVP and Sensitivity Analysis for a Brewpub. As described in “Business in Action 3.2”, three entrepreneurs were looking for private investors and financial institutions to fund a new brewpub near Sacramento, California. This brewpub was to be called Roseville Brewing Company (RBC).
Brewpubs provide two products to customers: food from the restaurant segment, and freshly brewed beer from the beer production segment. Both segments are typically in the same building, which allows customers to see the beer brewing process.
After months of research, the three entrepreneurs created a financial model that showed the following projections for the first year of operations:

In the process of pursuing capital (cash) through private investors and financial institutions, they were asked several questions. The following is a sample of the questions most commonly asked:
It became clear that the initial financial model was not adequate for answering these questions. After further research, the entrepreneurs created another financial model that provided the following information for the first year of operations. (Notice that operating profit of $302,212 is the same as in the first model.)

Required:
Round your answers to the nearest hundredth of a percent and nearest dollar where appropriate. (An example for percentage calculations is 0.434532 = 0.4345 = 43.45 percent; an example for dollar calculations is $378.9787 = $379.)
- What is the break-even point?
- What sales dollars will be required to make $200,000? To make $500,000?
- Is the product mix reasonable? (Beer tends to have a higher contribution margin ratio than food, and therefore product mix assumptions are critical to profit projections.)
- What happens to operating profit if the product mix shifts?
- How will changes in price affect operating profit?
- How much does a pint of beer cost to produce?
- What were potential investors and financial institutions concerned about when asking the questions listed previously?
- Why was the first financial model inappropriate for answering most of the questions asked by investors and bankers? Be specific.
- Suppose you are deciding whether to invest in RBC. Which financial ratio would you use to check the reasonableness of RBC’s projected operating profit as compared with that of similar businesses?
- Why is it difficult to answer the question “How much does a pint of beer cost to produce?” Which costs would you include in answering this question?
-
Perform CVP analysis by answering the following questions:
- What is the break-even point in sales dollars for RBC?
- What is the margin of safety in sales dollars for RBC?
- Why is it not possible for RBC to find the break-even point in units?
- What sales dollars would be required to achieve an operating profit of $200,000 and of $500,000? What assumptions are made in these calculations?
- Assume total revenue remains the same, but the product mix changes so that each of the three revenue categories is weighted as follows: food 70 percent, beer 25 percent, other 5 percent. Prepare a contribution margin income statement to reflect these changes. How will this shift in product mix affect operating profit?
- Although the financial model is important, what other strategic factors should RBC and its investors consider?




