2.5: End-of-Chapter Exercises
- Page ID
- 51328
Questions
- Define “accounts receivable.”
- How is the “net realizable value” of accounts receivable determined?
- Name three factors a company might consider when trying to determine the amount of accounts receivable that will be ultimately collected.
- What does the account “allowance for doubtful accounts” represent?
- Define “contra account.”
- When is bad debt expense recorded?
- Why do companies set up the allowance for doubtful accounts instead of just decreasing accounts receivable for any expected uncollectible balances?
- What entry does a company make to write off a specific account that has proven to be uncollectible?
- Give two reasons why accountants do not restate prior year statements when estimations are not exact.
- Name the two most popular approaches to estimating uncollectible accounts and briefly explain each.
- What is the purpose of a company having an accounts receivable subsidiary ledger?
True or False
- ____ Companies use two separate accounts in order to report accounts receivable at its net realizable value.
- ____ Bad debt expense is reported on the balance sheet as a contra account to accounts receivable.
- ____ The matching principle says that expenses should be recorded the same period as the revenues they help generate.
- ____ The net accounts receivable number on the balance sheet represents the exact amount the company will collect in cash.
- ____ All companies perform their estimation of uncollectible accounts in the same manner.
- ____ Frequently, bad debt expense and the ending balance in the allowance for doubtful accounts will differ.
- ____ The older a receivable, the less likely it is to be collected.
- ____ To make statements more accurate, bad debt expense is recorded when a specific account is deemed uncollectible and written off.
Multiple Choice
-
Which of the following would not be used to help a company determine the net realizable value of its accounts receivable?
- Industry averages and trends
- The company’s ability to pay its own debts
- Current economic conditions
- Efficiency of the company’s collection procedures
-
Which principle states that expenses should be recorded in the period in which they help generate revenues?
- Matching principle
- Going concern principle
- Cost/benefit analysis
- Measurement principle
-
SunFun Company manufactures lawn furniture that is sold to retailers like big box home improvement stores. During October 20X1, SunFun sold furniture to Home Place on account in the amount of $40,000. At the end of 20X1, the balance was still outstanding. In January 20X2, SunFun decided to write off this particular account as it did not appear the balance would ever be collected. Choose the correct journal entry for this transaction below.
-
Debit allowance for doubtful accounts 40,000 and credit accounts receivable 40,000.
-
Debit bad debt expense 40,000 and credit allowance for doubtful accounts 40,000
-
Debit bad debt expense 40,000 and credit accounts receivable 40,000
-
Debit cash 40,000 and credit accounts receivable 40,000
-
-
Ornate Inc. ended 20X3 with $400 in allowance for bad debts. In 20X4, Ornate wrote off $360 in accounts receivable that appear to be uncollectible. At the end of 20X4, Ornate recorded bad debt expense of $330. What is the balance in the allowance for doubtful accounts at the end of 20X4?
- $370
- $730
- $60
- $690
-
Gladson Corporation accrues bad debt expense using the percentage of sales method. At the end of the year, Gladson has $450,000 in accounts receivable and $4,000 (credit balance) in its allowance for doubtful accounts before any entry is made for bad debts. Sales for the year were $1,900,000. The percentage that Gladson has historically used to calculate bad debts is 1 percent of sales. Which of the following is true?
- Gladson’s bad debt expense for the year is $500.
- The percentage of sales method is designed to achieve an accurate balance sheet presentation of the net realizable value of accounts receivable.
- Gladson would report an allowance for doubtful accounts of $23,000.
- Gladson would need to make an adjustment because the $4,000 remaining balance in the allowance for doubtful accounts indicates they estimated wrong last year.
Problems
-
Nuance Company had net credit sales for the year of $950,000. Nuance estimates that 1 percent of its net credit sales will never be collected.
- Prepare the entry to record Nuance’s bad debt expense for the year.
- Nuance had accounts receivable of $180,000 at the end of the year. Show how the net accounts receivable balance would be reported on the balance sheet. Assume that the allowance for doubtful accounts had a beginning balance of zero.
- Why is A/R shown at net rather than just showing the full amount?
-
Assume that Nuance in number 1 above used the percentage of receivables method to estimate uncollectible accounts instead of the percentage of sales method. Nuance assumes that 3 percent of accounts receivable will never be collected.
- Prepare the entry to record Nuance’s bad debt expense for the year.
- Show how the net accounts receivable balance would be reported on the balance sheet. Assume that the allowance for doubtful accounts had a beginning balance of zero.
- Why are companies allowed to choose between methods of estimating bad debts instead of being required to use one method?
-
Ray’s GamePlace sells all the hottest gear and video games. On January 1, 20X7, Ray’s had the following account balances:

- During 20X7, Ray’s wrote off $5,000 in uncollectible accounts. Make this journal entry.
- During 20X7, Ray’s made credit sales of $148,000 and collected $116,000 of accounts receivable. Record these journal entries.
- At the end of the year, Ray’s determines that approximately 5 percent of its ending accounts receivable balance will not be collected. Ray’s uses the percentage of receivables method of calculating bad debts. Make the necessary journal entry.
4. Accounts receivable-trade in the Consolidated Balance Sheets is presented net of allowances for bad debts of $26,001 on December 31, 2022.
Accounts receivable-trade in the Consolidated Balance Sheets is presented net of allowances for bad debts of $26,001 on December 31, 2022.
The above information was provided by Hershey Company in its financial statements for year ended December 31, 2022. Answer the following about what is being communicated by the Hershey Company about accounts receivable:
a. What is the total amount owed by customers of Hershey for their purchases from Hershey as of the end of 2022?
b. What is the dollar amount that Hershey does not plan to collect based on their estimate of bad debts at the end of 2022?
c. What percentage of the total accounts receivable does Hershey plan on not collecting based on their estimate at the end of 2022? Round to a tenth of a percent.
d. When starting 2023, what amount should Hershey use as the beginning balance in the Accounts Receivable T account?
Comprehensive Problem
This problem will carry through several chapters, building in difficulty. It allows students to continuously practice skills and knowledge learned in previous chapters.
Recall in Chapter 1 that Leon Jackson started Webworks, a Web site design and maintenance firm. You helped him prepare his adjusted trial balance for June. We are going to continue with this problem, preparing Webworks financial statements for July.
Here are Webworks financial statements as of June 30.


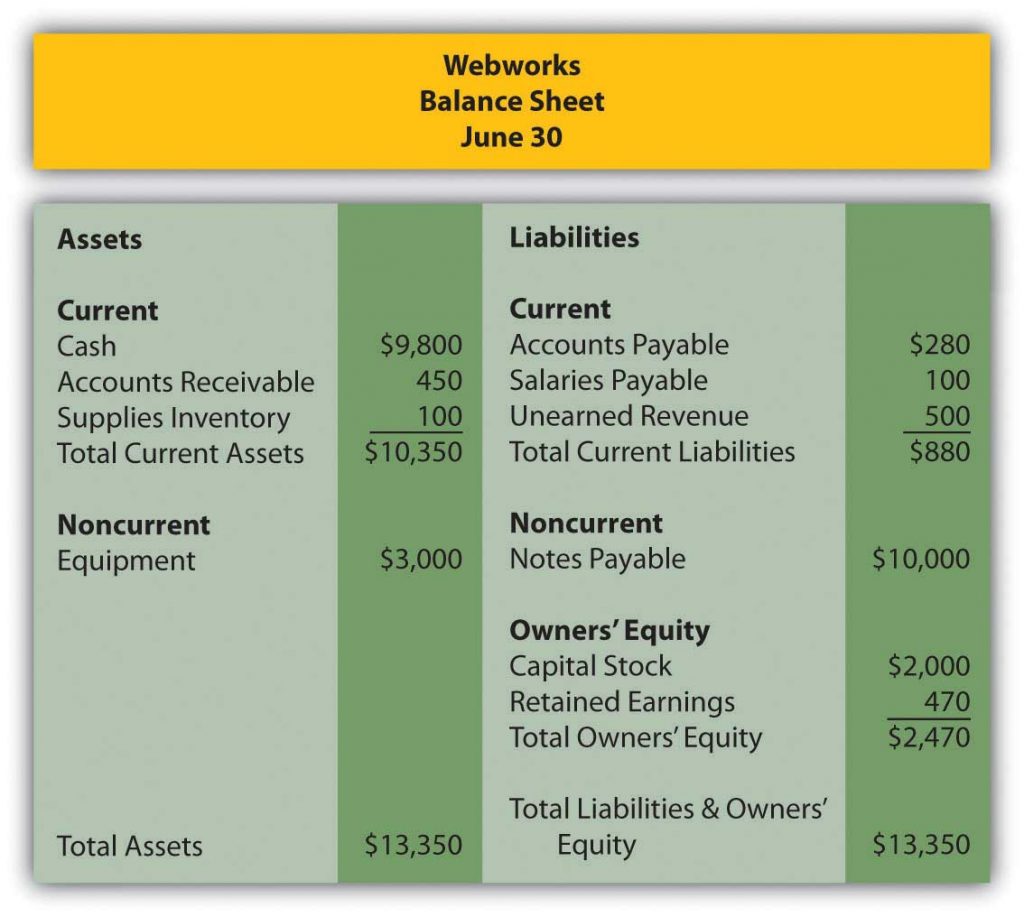
The following events occur during July:
a. Webworks purchases additional equipment for $4,000 cash.
b. Webworks purchases supplies worth $90 on account.
c. Webworks pays off its accounts payable and salaries payable from June.
d. Webworks starts and completes four more Web sites and bills clients for $1,800.
e. Recall that in June, Webworks received $500 in advance to design a restaurant Web site. Webworks completes this site during July.
f. Webworks collects $1,200 in accounts receivable.
g. Webworks pays Nancy $500 for her work during the first three weeks of July.
h. Webworks receives $200 in advance to work on a Web site for a local dry cleaner and $300 in advance to work on a Web site for a local vet. Work will not begin on the Web sites until August.
i. Leon’s parents have decided to charge rent after seeing how successful his business is and how much space it is taking up in their house. They all agree that rent will be $200 per month. Webworks pays $600 for July, August, and September.
j. Webworks pays taxes of $300 in cash.
Required:
A. Prepare journal entries for the above events.
B. Post the journal entries to T-accounts.
C. Prepare an unadjusted trial balance for Webworks for July.
D. Prepare adjusting entries for the following and post them to your T-accounts.
k. Webworks owes Nancy $200 for her work during the last week of July.
l. Leon’s parents let him know that Webworks owes $150 toward the electricity bill. Webworks will pay them in August.
m. Webworks determines that it has $50 worth of supplies remaining at the end of July.
n. Prepaid rent should be adjusted for July’s portion.
o. In June, Webworks designed a site for Pauline Smith, but has not yet been fully paid. Leon believes the company may not be able to collect all of its accounts receivable. A local CPA helps Leon determine that similar businesses report an allowance for bad debt at an average of 10 percent of their accounts receivable. Webworks will use this method. Make the bad debt adjustment for Webworks.
E. Prepare an adjusted trial balance.
F. Prepare financial statements for July.

