6.4: Budgets and Revenues from Usage
- Page ID
- 21141
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)
In addition to the cost implications of different levels of infrastructure usage, there is often a revenue effect. Many infrastructure systems obtain revenues from user fees such as power sales or gasoline taxes. In turn, budgets for infrastructure maintenance and rehabilitation rely upon these revenues. The alternative to using user fees is to rely on general taxation of some sort, but this is only feasible for public infrastructure.
Generally, user fees can be set at any level. A few cases of user fee strategies are of interest:
- Set user fees equal to the short run average total cost of providing the infrastructure. In this case, the infrastructure provider is fully funded and compensated for the infrastructure service costs.
- Set user fees equal to an amount that maximizes total revenue. This strategy can be pursued with an optimization problem to maximize revenue (\(p*q\) where \(p\) is user fee and q is equilibrium usage) subject to the demand function (\(q = f(p,x)\) where \(f(p,x)\) is a demand function with usage dependent upon the user fee and other factors \(x\)). Even with a maximizing revenue strategy, usage may not be sufficiently high to cover all agency costs. For example, the Pennsylvania turnpike has increased tolls every year from 2008 to 2016 and made transfer payments to the Commonwealth of Pennsylvania, but the managers feel that the revenues are insufficient in the long run to maintain the system effectively and make required transfer payments (Pittsburgh Post-Gazette, 2016).
- Set user fees in accordance with user’s willingness-to-pay. Demand curves reflect an individual’s willingness-to-pay for infrastructure services. If the user cost function shifted up in Figure 6.3.3, some usage would disappear but a remaining amount of usage demand would continue at higher user cost. With a single user cost, the revenue would be roughly \(q_e * p_e\) in figure 6.3.3 (less any user costs incurred directly rather than as a service price). Perfect price discrimination would gain revenue equal to the complete area under the demand curve in Figure 6.3.3 (again less any user costs incurred directly). However, individuals don’t usually reveal their willingness-to-pay for service and there are restrictions on discriminating among different types of users. Indirect methods can be adopted, however, such as lower airline fares for earlier purchases or for trips involving a Saturday night stay. Business travelers with a higher willingness-to-pay tend to make late purchases and not stay at destinations over a weekend.
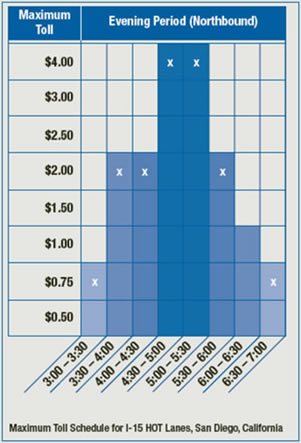
- Set user fees equal to short run marginal cost. This is a common economics prescription because this strategy will minimize overall costs as long as the short run marginal cost function includes all relevant social costs (including externalities). Users would be paying exactly the cost associated with their service use. Unfortunately, it is difficult to impose short run marginal cost pricing exactly since demand fluctuates so much. An example of approximating this policy appears in Figure 6.4.1, where toll on a roadway in San Diego CA increase during peak periods of travel demand. By increasing tolls, some users would be diverted from the roadway and congestion costs avoided.