5.3: Integer Optimization for Infrastructure Management

In many infrastructure management optimization problems, the decision variables may be restricted to integer values. For example, in the previous section, decision variables were defined as undertaking a particular maintenance or rehabilitation action j on a roadway segment i. While the decision variable could be a fraction, so that only part of the roadway segment undergoes a maintenance activity, it is more natural to manage the segment as a whole and wish to have binary decision variables that are zero or one.

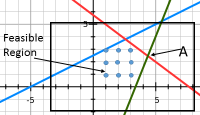
Integer constraints impose several problems in obtaining optimal solutions. For linear programming, optimal values could be sought on the extreme corners of the feasible region. With integer value constraints, the optimal solution may be inside the feasible region. As illustrated in Figure 5.3.1, feasible integer values are shown as dots within a region satisfying the linear constraints. The only feasible solution on an extreme corner would be the solution \(x1 = 0\) and \(x2 = 0\). Point A marked on the figure would have fractional values of \(x1\) and \(x2\).

Figure \(\PageIndex{1}\): Illustration of Integer Feasible Solutions to a Linear Optimization Problem.

One approach to integer programming is to ignore the integer constraints and solve the problem as a linear program. With binary restrictions and integer parameters and constrain values, this approach works frequently to give optimal, binary solutions. A fractional decision variable value might be rounded by a manager to obtain a very good but not necessarily strictly optimal solution in this approach. Given the uncertainty in costs and action effects, the rounding might not affect the overall infrastructure performance.

More formal methods of obtaining optimal integer solutions also exist. A popular approach is ‘branch-and-bound.’ In this process, an initial linear solution is obtained, and then constraints are added to force the solution to be an integer. For example, in Figure 5.3.1, if point A was obtained as the optimal solution, and good additional constraint might be to require \(x1\) to be 3 or less: \(x1 \leq 3\). This would be a new ‘branch’ for the problem solution with a ‘bound’ that cuts out a portion of the region that does not contain integer values. Adding constraints in this fashion would continue until an integer-valued optimal solution is obtained.

‘Branch and bound’ or other integer programming approaches are part of most popular optimization software, including the Solver program for the EXCEL spreadsheet. Integer constraints are specified when problems are input to the programs. However, solving integer programs requires more calculation time than comparably sized linear programs. While linear programs with thousands of decision variables can be easily solved, integer programs may be realistically limited to hundreds of decision variables. Still, this could well a useful range for many infrastructure management problems.

The ‘traveling salesman’ problem is a classic example of an integer programming problem. The problem is to develop a round-trip tour that visits each and every one of a set of cities exactly once with minimum travel distance. For infrastructure management, a tour of this type might be formulated by an inspector of different infrastructure components or a maintenance worker with a set of assigned jobs. In these problems, ‘cities’ would be inspection or job sites. The UPS routing software for delivery trucks mentioned in the introduction to this chapter solves this problem (UPS 2016). Variations of the problem can be found in manufacturing (where ‘cities’ may be spots on a chip) and DNA sequencing.

A decision variable for the traveling salesman problem might be \(x_{ij}\) which is 0 if the trip from \(i\) to \(j\) is not on the tour and 1 if the trip from \(i\) to \(j\) is on the tour. The objective function would be to sum the distance (or cost) of the trip from \(i\) to \(j\) multiplied by the \(x_{ij}\) values. Only those trips which are part of the tour would incur any distance and affect the value of the objective function. Constraints require that there is exactly one departure from each city (so the sum of the \(x_{ij}\) from I equals one) and exactly one arrival at each city. Additional constraints are needed to ensure that the tour is complete (that is, the tour doesn’t have multiple disjoint circuits). Finally, the decision variables \(x_{ij}\) are restricted to zero or one.

Numerous specialized algorithms have been developed for the traveling salesman problem. In practice, heuristic approaches can obtain very good (but not necessarily optimal) solutions.