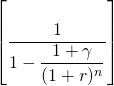10: Homogeneous Terms
- Page ID
- 12755
Assuming reinvestment rate is investments IRR After completing this chapter, you should be able to: (1) consistently rank one-time investments using internal rate of return (IRR) or net present value (NPV) methods; (2) find time adjusted cash flow averages called annuity equivalents (AE); (3) use AE to find the optimal life of a repeatable investment; and (4) use capitalization rates to find the present value of long-lived investments and repeatable investments.
To achieve your learning goals, you should complete the following objectives:
- Learn appropriate methods for ranking one-time investments with unequal terms using IRR or NPV ranking criteria.
- Learn how to represent the time adjusted average of an investment’s cash flow using AE.
- Learn how IRR and NPV methods may provide conflicting optimal replacement ages for repeatable investments.
- Learn how to use an investment’s cash flow patterns and its AE to determine the optimal life of a repeatable investment.
- Learn how to find the present value of future earnings from repeatable investments using the capitalization formula.
Introduction
One-time investments. In the previous chapter, we developed methods for ranking one-time mutually exclusive investments with unequal initial and periodic sizes. In that effort, we employed a simplifying assumption: that the terms of the competing challengers and the defender were equal. This assumption is frequently violated. Not all challengers and defenders have equal terms or economic lives. Therefore, we develop methods for ranking one-time mutually exclusive challengers of unequal terms which is the first goal of this chapter. An important characteristic of one-time investments is that owning a one-time investment does not require replacement in order to invest in a similar investment.
Repeatable investments. Some investments provide essential services. As a result, when they wear out, they need to be replaced (think of a light bulb). What replaces the existing investment may be an identical, improved, or remodeled version of the original investment. We call these investments that require replacement, repeatable investments because they are owned in sequence rather than simultaneously. Examples of repeatable investments include orchards, breeding livestock, roofs on houses, and equipment. Since repeatable investments are owned in sequence, we must determine what is the optimal time to replace a repeatable investment.
AE and cash flow patterns. Finding the optimal life of a repeatable investment requires that we review the concept of a time-adjusted average cash flow, an AE. AE, of course, change as new periods of cash flow are included in its calculation. Using AE for different time periods and patterns of cash flow, we can determine the optimal life of the investment.
Capitalization rates. To rank repeatable investments, we must value the present value of the original investment and their future replacement’s cash flow. We accomplish this task by using capitalization rates, a common tool used by appraisers to value long-term investments.
Present Values and Capitalization Rates
The economic life and term of an investment. The term of an investment is the number of periods the financial manager expects to manage an investment. The economic life of an investment is the number of periods the investment is expected to generate cash flow. The PV of an investment for an individual depends on its cash flow during the term of the investment plus its liquidation value. The liquidation value of the investment depends on its economic life. Therefore, to estimate the present value for an investment, we must find the discounted present value of all future cash flows. In practice, we often estimate the present value of an investment using the capitalization formula.
The capitalization formula and capitalization rate. Consider a challenging investment that earns R constant cash flow dollars for n period and is liquidated at the end of the nth period for Vn. We assume that the defender funding the investment has an IRR of r. We write the maximum bid (minimum sell) price PV model that equates V0 to its discounted future earnings over a term of n periods discounted by its defender’s IRR as:
(10.1)
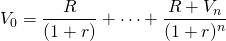
Now assume that the second owner of the investment has the same earnings expectations as the first owner of the durable so that we can write:
(10.2)
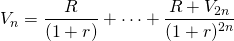
Finally, substituting for Vn in Equation \ref{10.1} the right hand side of Equation \ref{10.2} we obtain:
(10.3)
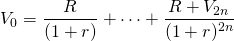
And if the investment’s salvage value were continually exchanged with its expected cash flows we could write:
(10.4)
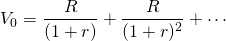
Clearly, the farther away from the present is the constant cash flow R, the less it contributes to the present value of the investment. To demonstrate the diminishing contributions of future cash flow, note how the value of discount rate that multiplies R decreases with n. To illustrate we let r = 10%, R=100, and alternative values of n.
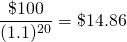
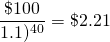
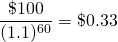
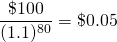
And
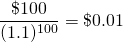
So what is the sum of an infinite stream of constant payments R discounted by r percent? To find that sum, multiply both sides of Equation \ref{10.1} by (1 + r) and subtract from the result the original equation:
(10.5)
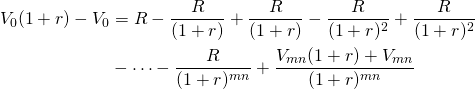
After subtracting and simplifying and letting m get very large, we find the sum of the infinite series to equal:
(10.6)
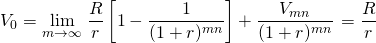
The far right-hand side of Equation \ref{10.6} we refer to as the capitalization formula where the investment’s AE is equal to R divided by the defender’s IRR equal to r, the capitalization rate. The capitalization formula allows us to relate the present value of all future cash flow to the value of the investment.
(10.7)
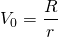
To illustrate the capitalization formula, suppose that you purchase an annuity for $100 that pays you and your heirs $5 a year forever. The capitalization formula for this investment is equal to:
(10.8)

If we knew the investment’s initial value and its infinite stream of AEs, we could always estimate the capitalization rate equal to:
(10.9)
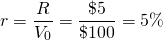
Comments about the capitalization formula and capitalization rate. In textbooks and references to the capitalization rate, it is often expressed as:
(10.10)
Then when practitioners implement the capitalization formula, Equation \ref{10.9}, they estimate R as the first period’s net cash flow and an industry capitalization rate for r. For example, if the industry standard were 5%, we would write the capitalization formula that estimates the maximum bid price for the investment as:
(10.11)
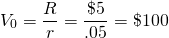
PV models and capitalization formulas. The capitalization formula is a PV model. The unknown variable in the capitalization formula identifies the kind of PV model represented. If the unknown variable is the discount rate or the capitalization rate r, the capitalization formula is an IRR model. Most often, capitalization formulas solve for V0 making them maximum bid (minimum sell) type models.
So what have we learned? We learned that we can best understand the capitalization formula and the capitalization rate in the context of a PV model. Despite its various descriptions in applied publications, the capitalization formula is the AE of the investment over its economic life divided by defender’s IRR.
More Complicated Capitalization Formulas
In the discussion to this point, we implemented the capitalization formula by assuming that the future cash flow were constants, AEs. This of course, is rarely the case. We now ask: how can we find the capitalization formula if future cash flow are expected to increase (decrease) at g% over time as you might expect on rental property? To answer this question we return to our PV model.
Suppose that we wanted to find the capitalization formula for an investment whose cash flow are expected to increase (decrease) at an average rate of g percent (g < 0 percent). Then the capitalization formula that accounts for R is increasing (decreasing) at rate g (g < 0) as:
(10.12)
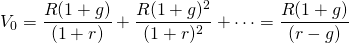
Now the capitalization rate, the defender’s IRR is equal to: (r – g)/(1 + g). We write the capitalization rates depending on alternative values of g and r = 10 in Table 10.1
Table 10.1a. Alternative percentage capitalization rates (r – g)/(1 + g) depending on alternative values of g > 0 and r
| g = 0% | g = 1% | g = 2% | g = 3% | g = 4% | g = 5% | |
| r = 10% | 0.1 | 0.089 | 0.078 | 0.068 | .058 | 0.048 |
| r = 9% | 0.09 | 0.079 | 0.069 | 0.058 | 0.048 | 0.038 |
| r = 8% | 0.08 | 0.069 | 0.059 | 0.049 | 0.038 | 0.029 |
| r = 7% | 0.07 | 0.059 | 0.049 | 0.039 | 0.029 | 0.019 |
| r = 6% | 0.06 | 0.050 | 0.039 | 0.029 | 0.019 | 0.01 |
Table 10.1b. Alternative percentage capitalization rates (r – g)/(1 + g) depending on alternative values of g < 0 and r
| g = 0% | g = –1% | g = –2% | g = –3% | g = –4% | g = –5% | |
| r = 10% | 0.10 | 0.111 | 0.122 | 0.134 | 0.146 | 0.158 |
| r = 9% | 0.09 | 0.101 | 0.112 | 0.124 | 0.135 | 0.147 |
| r = 8% | 0.08 | 0.091 | 0.102 | 0.113 | 0.125 | 0.137 |
| r = 7% | 0.07 | 0.081 | 0.092 | 0.103 | 0.115 | 0.126 |
| r = 6% | 0.06 | 0.071 | 0.082 | 0.093 | 0.104 | 0.116 |
Ranking One-time Investments with Unequal Terms using NPV Models
Notation. Before proceeding to the first focus of this
chapter, we confirm the notation used earlier and which will be
used again in this chapter. The mathematical notation will describe
two challenging investments and a defender. We assume that the
initial investment sizes are equal to V0. The
defender’s IRR for the two investments is r. The term of
investments one and two are n1 and
n2 respectively. Periodic cash flows for
investments i = 1, 2 in period t = 1, …,
ni can be expressed as 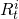 .
And the vector of cash flows is represented as:
.
And the vector of cash flows is represented as: 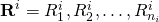 for i = 1, 2.
for i = 1, 2.
Finally, we define the sum S of
compounded periodic cash flows at rate r as: 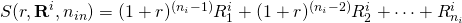 .
We also define the sum of periodic cash flows compounded at the
investment’s IRR as:
.
We also define the sum of periodic cash flows compounded at the
investment’s IRR as: 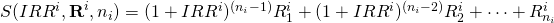 .
Note that the value of the function S depends on three variables
defined in the equation: the reinvestment rate r or
IRRi, the vector of periodic cash flows
.
Note that the value of the function S depends on three variables
defined in the equation: the reinvestment rate r or
IRRi, the vector of periodic cash flows 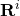 ,
and the term of the investment ni.
,
and the term of the investment ni.
Sufficient conditions for consistently ranking mutually exclusive one-time investments using IRRs and NPVs. We discovered in Chapter 9 that there are two sufficient conditions for consistently ranking investments using NPVs and IRRs—assuming their terms were equal. These two sufficient conditions are equal initial investment sizes and equal periodic cash flows except in their common last period.
In this chapter we will assume that initial sizes of investments are equal. However, we will allow for differences in periodic cash flows because investment terms differ. As a result, we can no longer be sure that the NPVs and IRRs rank investments the same. To solve the problem of unequal periodic cash flows, we need to rationalize investment term differences. Our focus in the first part of this chapter is on how to create equal terms and periodic cash flows except for the last period for mutually exclusive challengers.
Compounding and discounting by the same rate are offsetting operations. Essential to rationalizing term differences is the obvious fact that NPVs for investment one and two compounded and discounted at rate r have the same value as their original NPV function. We demonstrate this point using the following equations. For investment one, the result is:
(10.13a)
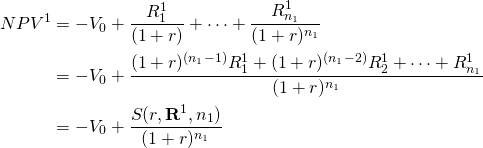
Similarly, for investment two:
(10.13b)
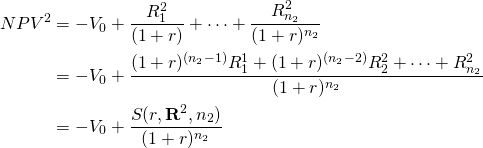
What equations 10.13a and 10.13b illustrate is the obvious: multiplying by one, the compound rate divided by the identical discount rate, cannot change the value of what is being multiplied.
In Chapter 9, we created equal periodic cash flows by reinvesting the periodic cash flows until the last period, creating MNPV and MIRR models. Then we learned that if the reinvestment rate was equal to the discount rate that NPV and MNPV and IRR and MIRR models produced identical results because reinvesting and discounting by the same rate are offsetting operations. What we learn in this chapter confirms this principle, that reinvesting and discounting by the same rate are offsetting operations. Furthermore, this principle can be used to resolve differences in investment terms.
Resolving term differences. We can
convert challengers to the same term by reinvesting and discounting
their cash flow to a common term. The compound factor that converts
the periodic cash flows and the discount rate from period
n2 to n1 is 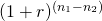 .
This is applied to the extreme right-hand side of equation (10.13b)
resulting in the expression:
.
This is applied to the extreme right-hand side of equation (10.13b)
resulting in the expression:
(10.14)
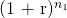
Equation (10.14) confirms once again that compounding and discounting by the same rate are offsetting operations even when used to extend the term of investments. Nevertheless, by compounding and discounting by the same rate (multiplying by one), we convert the term of investment two to the term of investment one without changing the value of the function. It is still equal to the original NPV equation.
The rankings of investments one and two—assuming their reinvestment rates and discount rate are the defender’s IRR, r—can be expressed as:
(10.15)
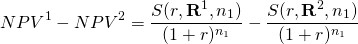
Clearly, the only difference between the two NPVs are their vector of cash flow since they have equal initial investments, discount (reinvestment) rates, and terms.
Ranking One-time Investments with Unequal Terms using IRR Models.
Now suppose that we replace the reinvestment rate r in equations 10.13a with the IRR of challenger one equal to IRR1. Also assume that we replace the reinvestment rate r in 10.13b with the IRRs of challenger two, IRR2. We continue to assume that the discount rate for both investments is the defender’s IRR. The revised MIRR ranking equation can be expressed as:
(10.16)

IRR and NPV Models for Analyzing Repeatable Investments
The two preceding sections resolve term differences by assuming the reinvestment rates were either the defender’s or the challengers’ IRRs. The problem is that we can no longer be certain that the NPV and IRR methods rank the challengers consistently since we violated the common reinvestment rate assumption—the reinvestment rates were the challengers’ own IRRs. If we allow each investment to reinvest in itself, we lose our consistency guarantee.
Another problem using IRR methods besides losing consistency with NPV rankings is that methods for finding the optimal term involve finding the term with the greatest IRR instead of finding the term with the largest AE. This complicates an already complicated subject.
For these and several other reasons, in the remainder of this chapter we will analyze repeatable investments using NPV model assumptions, the most notable of which is that the reinvestment rate is the defender’s IRR common to both challengers. To be clear, we could assume a common defender’s IRR or each challenger’s IRR but having more than one challengers’ IRR may produce inconsistent rankings and asymmetry in exchanges. Were we to assume a still different reinvestment rate besides these, the defender’s or the challengers’ IRR would imply there exists another challenger besides those being considered and, if so, should be considered as a separate challenger.
So in what follows, we assume that earnings from the challengers are reinvested in the defender and asymmetry between exchanges of dollars between time periods. In the next section we begin building the AE tool using NPV assumptions required to analyze repeatable investments.
Present Value (PV) Models and Averages
Ranking investments using their annuity equivalents (AE). Referring to our previous analogy, trying to rank two investments of different terms would be like trying to rank horses in a race in which they each ran different distances. If we did indeed wish to compare two horses that ran different distances, at least we could compare their average speed—their average speed per mile. Then, even though the comparison might not be perfect, at least the comparisons would be compatible.
This is the essence of ranking investments by their time adjusted averages, referred to earlier as their annuity equivalents (AE). Ranking investments using the AE will be essential when we find the optimal age of repeatable investments.
Arithmetic means, expected values, geometric means and AE. There are several measures of central tendency in a numeric series that include arithmetic means, expected values, and geometric means. An example of an arithmetic mean or average follows. Consider three numbers 3, 5, and 7. The average of these numbers can be calculated by dividing their sum by 3 since there are three numbers: (3 + 5 + 7) / 3 = 5. This is the average of this series. Now suppose we wanted to find the mean of the three numbers weighted by their probability of occurring. If the probability of 3 occurring were 25%, if the probability of 5 occurring were 25%, and the probability of 7 occurring were 50%, then the expected value of the series would be: [(.25)3] + [(.25)5] + [(.5)7] = 5.50. This is the weighted average or expected value of the series.
Next consider an example of a geometric mean.
Consider three rates of return: 105%, 110% and 115%. The geometric
mean is that number which, when multiplied together three times,
equals the product of 105%, 110%, and 115%: [(1.05)(1.10)(1.15)] =
(1.0991)3. Alternatively, the geometric mean is
![]() where n = 3 because there are three numbers in the series.
Note that the geometric mean is not equal to the arithmetic mean:
[(1.10 + 1.11 + 1.12)] / 3 = 1.11. It is also not necessarily equal
to the expected value.
where n = 3 because there are three numbers in the series.
Note that the geometric mean is not equal to the arithmetic mean:
[(1.10 + 1.11 + 1.12)] / 3 = 1.11. It is also not necessarily equal
to the expected value.
To illustrate AE, the constant R in Equation
\ref{10.9} is an AE whose present value sum equals the present
value of the sum of discounted cash flow 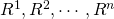 .
.
(10.17)
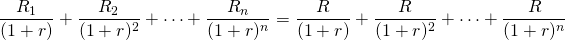
For example, consider the AE in the following problem:
(10.18)
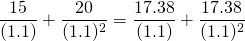
On the left hand side of Equation \ref{10.17} is a stream of unequal periodic cash flow. On the right hand side of Equation \ref{10.17} is a stream of equal periodic cash flow each of which is an AE. The important fact, however, is that the discounted AE on the right-hand side of Equation \ref{10.17} equals the discounted periodic cash flow on the left-hand side of Equation \ref{10.17}. The AE for the series on the right-hand side of Equation \ref{10.17} is 16.85. We demonstrate how to find an AE using Excel as follows.
Table 10.2a. How to find an
AE for an irregular stream of cash flow
Open Table 10.2a. in Microsoft Excel
| B6 | Function: | =NPV(B2,B3:B4) | |
| A | B | C | |
| 1 | How to find an AE for an irregular stream of cash flow | ||
| 2 | rate | 0.1 | |
| 3 | R1 | 15 | |
| 4 | R2 | 20 | |
| 5 | nper | 2 | |
| 6 | NPV | $30.17 | NPV(rate, R1:R2) |
Calculating AE from an irregular stream of cash flow is a two-step procedure. The first step is to find the net present value (NPV) of the irregular cash flow stream. We illustrate this step using Excel’s NPV function. In our example, the NPV of $15 received at the end of period one and $20 received at the end of period two is $30.17.
The next step is to find the AE, a constant payment, for the NPV equal to $30.17. Using Excel’s PMT function we find the AE for an NPV of $30.17 equal to $17.38. We display the Excel solution below.
Table 10.2b. How to find an
AE for an irregular stream of cash flow
Open Table 10.2b. in Microsoft Excel
| B7 | Function: | =PMT(B2,B5,B6,,0) | |
| A | B | C | |
| 1 | How to find an AE for an irregular stream of cash flow | ||
| 2 | rate | .1 | |
| 3 | R1 | 15 | |
| 4 | R2 | 20 | |
| 5 | nper | 2 | |
| 6 | NPV | $30.17 | NPV(rate,R1:R2) |
| 7 | AE | ($17.38) | PMT(rate,nper,NPV,,0) |
Some observations on NPV and AE rankings. Consider an NPV model and its value expressed as the present value of a series of AE in Equation \ref{10.19}. Since the present value of the AE is equal to the NPV of the investment, then the two sums must provide equal NPV rank. Important to note, however, is that it is the present value of the series of AE payments that is equal to the NPV, while a number of unequal payments could equal the same NPV. Therefore, there is a direct relationship (i.e. they both go up or down together) between NPVs and AEs. Furthermore,
(10.19)
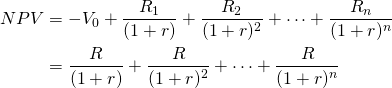
any change in NPV must be matched by a corresponding change in the AE and in the same direction. For any two investments of equal size and term, and where investment one has a larger NPV than investment two, then investment two must increase its AE in order for it to equal the higher NPV amount. We illustrate this point in more detail.
Consider again the expression:
(10.20)
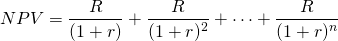
Then, suppose the term of the model in Equation \ref{10.20} is increased by one period. Then the equality in Equation \ref{10.20} no longer holds:
(10.21)
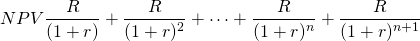
To preserve the equality in Equation \ref{10.20},
the AE equal to R must be decreased by some amount
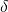 to reestablish the equality allowing us to rewrite the earlier
equality:
to reestablish the equality allowing us to rewrite the earlier
equality:
(10.22)
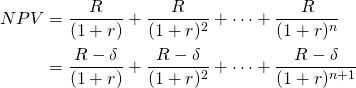
Numerical Demonstrations
Term difference and inconsistent rankings. Consider Table 10.3. Note that the two challengers are not periodic size consistent because they withdraw funds at different rates. Challenger one withdraws all of its earnings after one period. Meanwhile, challenger two withdraws some of its earnings in period one and the remainder in period two. As a result, the two investments have unequal terms.
In Table 10.3 panel a, we rank the two challengers using their NPV, IRR, and AE assuming that the discount rate and the reinvestment rate is 10%. In Table 10.3 panel b, we make the two challengers periodic size-consistent by reinvesting period one earnings for one period at the defender’s IRR. This operation also resolves term differences between the two investments.
Table 10.3. The Influence of periodic Size and Term Differences Created by Differential Withdrawals.
| Panel a. NPV, IRR and AE rankings assuming different periodic cash flows and terms for challengers one and two and a discount rate equal to the defender’s IRR of 10%. | ||||||
| Challengers | Initial Outlay | Cash Flows in period one | Cash Flows in period two |
NPV (rankings) |
IRR (rankings) |
AE (rankings) |
| C1 | $1,000 | $1,180 | $0 |
$72.73 (2) |
18% (1) |
$72.73 (1) |
| C2 | $1,000 | $160 | $1,160 |
$104.13 (1) |
16% (2) |
$60.00 (2) |
| Panel b. NPV, IRR, and AE rankings assuming equal periodic cash flows and terms for challengers one and two where equal periodic cash flows and terms are achieved by reinvesting period one cash flows at the defender’s IRR rate of 10% to a common ending period. NPV and IRR rankings after adjusting for term differences assuming a reinvestment rate of r. | ||||||
| Challengers | Initial Outlay | Cash Flows in Period one | Cash Flows in Period two |
NPVs and MNPVs (rankings) |
IRR (rankings) |
AE (rankings) |
| C1 | $1,000 | $0 | $1,180 (1.10) = $1,298 |
$72.73 (2) |
6.7% (2) |
$49.91 (2) |
| C2 | $1,000 | $0 | $160 (1.10) + $1,160 = $1,336 |
$104.13 (1) |
15.6% (1) |
$60.00 (1) |
| Panel c. NPV, IRR, and AE rankings assuming equal periodic cash flows and terms for challengers one and two where equal periodic cash flows and terms are achieved by reinvesting cash flows at the investments’ IRRs. The discount rate is assumed to equal the defender’s IRR of 10% | ||||||
| Challengers | Initial Outlay | Cash Flows in Period one | Cash flows in Period two |
NPV (MNPV) (rankings) |
IRR (rankings) |
AE (rankings) |
| C1 | $1,000 | $0 | $1,180 (1.18) = $1,392.40 |
$150.74 (1) |
18% (1) |
$86.66 (1) |
| C2 | $1,000 | $0 | $160 (1.16) + $1,160 = $1,345.60 |
$112.07 (2) |
16% (2) |
$64.57 (2) |
Term and periodic cash flow differences in Table 10.3 panel a produced inconsistent rankings using NPV versus IRR and AE methods. However, in Table 10.3 panel b, when term and periodic cash flow differences were eliminated except for the common last period through reinvesting at the defender’s IRR of 10%, NPV, IRR, and AE rankings were consistent. In Table 10.3 panel c, when term and periodic cash flow differences were eliminated through reinvesting at the challengers’ respective IRRs of 18% and 16%, NPV, IRR, and AE rankings were again consistent but changed from the rankings produced when the reinvestment rate was the defender’s IRR.
There are two things to be emphasized about Table 10.3. First, NPVs in panel a and panel b are the same even after adjusting for differences in periodic cash flows and terms. This is because the reinvestment rate was the defender’s IRR, and reinvesting and discounting cash flows are offsetting operations. Second, when we adjusted for periodic size inconsistencies using the investments’ IRRs as the reinvestment rate, NPVs changed but the investments’ IRRs were equal to their MIRRs in panels a and c. This is again the result of reinvesting and discounting by the same rate—the investments’ IRRs.
Alternative reinvestment rate assumptions. In Table 10.3, we made the first challenger into a two-period model by reinvesting its earnings at the defender’s IRR. Suppose the one-period challenger was available for investment in each period. In other words, suppose that challenger one could be repeated. Since challenger one is an investment of size $1,000, then only $1,000 of period one earnings could be reinvested in the one-period challenger. The difference between the challenger’s first-period earnings and $1,000 we assume will be invested at the defender’s IRR. The new investment problem is summarized in Table 10.4.
Table 10.4. Resolving Term Differences Between Two Challengers by Reinvesting $1,000 of Period One Earnings at its One-period IRR of 18% and Reinvesting other Funds at the Defender’s IRR of 10%.
| Challengers | Initial Outlay | Cash Flow in period one | Cash Flow in period two | NPV assuming defender’s IRR is 10% (rankings) | IRR
(rankings) |
AE (rankings) |
| C1 | $1,000 | $0 | $1,000 (1.18) + $180 (1.1) = $1,378 |
$138.84 (1) |
17.4% (1) |
$80.00 (1) |
| C2 | $1,000 | $0 | $1,160 + $160 (1.1) = $1,336 |
$104.13 (2) |
15.6% (2) |
$60.00 (2) |
The interesting result of Table 10.4 provides an example of a blended reinvestment rate not equal to either the defenders IRR of 10% or the investment’s own IRR but a weighted average of them both equal to 17.4% for investment one and 15.6% for investment two. However, viewing investment opportunities as combinations of investments in the defender and the challenger must be considered to be a new challenger with a unique reinvestment rate.
Using Annuity Equivalents (AE) to Rank Repeatable Investments
The difficulty of finding finite number of replacements to resolve term differences. In our previous example, we resolved term differences between a one-period investment and a two-period investment by repeating the first investment. Now suppose we have a more complicated term inconsistency problem. For example, assume challenger one’s term is 7 periods while challenger two’s term is 8 periods. Now repeating an investment one or several times won’t resolve term differences. Indeed, to resolve term differences in this problem would require that challenger one be repeated 8 times and challenger two be repeated 7 times. Now we have a 58-period model—which requires a lot of work.
Using Annuity Equivalents (AE) to rank repeatable investments. We can resolve term differences by calculating and comparing the AE of the investments, even though they have different terms. The reason we can use the AE to rank investments of different terms is because the annuity equivalent doesn’t change when you increase the term by repeating investments. Thus, the AE from one investment repeated 2, 3, 4, 7, 8, m, or an infinite number of times is the same. This is an important fact because the AE calculated over the lives of multiple (infinite) replacements can be compared to the AE of another repeatable investment and the two investments can be ranked by their difference.
We now support the claim that we can rank repeatable investments by their AE. We write the one-period model as:
(10.23a)
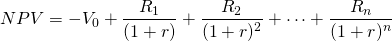
We write the NPV model with one replacement as:
(10.23b)
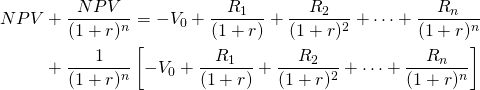
And we could write the NPV model with enough replacements to equalize their term as:
(10.23c)
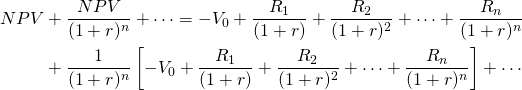
Next, factoring, we obtain:
(10.23d)
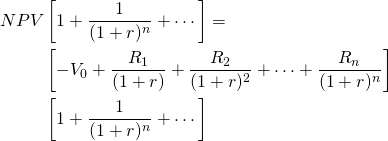
Then, canceling the two bracketed terms at the end of each equation, we regain our original one-investment problem:
(10.23e)
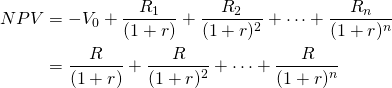
A numerical example that the AE for a single investment is equal to the AE calculated over two investments. Note that the same AE that solved the one-investment problem solves the multiple-replacement problem.
We demonstrate this result in Table 10.5 which calculates AE for one investment and then recalculates the AE for an investment and one replacement.
Table 10.5. Resolving Term Inconsistencies by Calculating AE for an Investment and the Investment and a Replacement Assuming Defender’s IRR is 10%
| Challenger | V0 | R1 | R2 | R3 | R4 |
NPV (rankings) |
IRR (rankings) |
AE (rankings) |
| C1 | $2,000 | $1,200 | $1,200 |
$82.64 (2) |
13.1% (1) |
$47.65 (1) |
||
| C1 plus replacement | $2,000 | $1,200 | $1,200 – $2,000 = –$800 | $1,200 | $1,200 |
$150.95 (1) |
13.1% (1) |
$47.65 (1) |
Table 10.5 illustrates the importance of AE rankings to resolve term (and size) inconsistencies for repeatable investments. Note first that term inconsistencies produce different NPVs. The NPVs are positive because the challenger earns a higher rate of return than the defender. Furthermore, collecting these returns for two challengers, the challenger and its replacement, earns more than just one investment. Hence, the NPV for the challenger and its replacement is greater than the NPV for just one challenger. On the other hand, both the IRR and the AE rank the investments the same, because their calculations are adjusted for the term of the investment. These results are also helpful because they confirm that the IRR of a single defender can be used to discount the challenger and still maintain consistency.
So what is our best advice? Resolve term inconsistencies for repeatable investments by calculating AE.
Finding AE that account for technologically improved replacements. Suppose that one of the challengers will be replaced by a technologically improved replacement that perhaps costs more, but also produces higher returns. For γ > 1 the investment problem takes the following form:
(10.24)
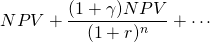
Including enough replacement to equalize terms, we find the sum of the discounted NPVs. Call this sum S which is equal to:
(10.25)
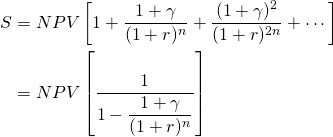
The details of the derivation are not included
here, but require nothing more that the summation of geometric
series. The interpretation of Equation \ref{10.25} is that
technological improvements result in NPV increases in the first
replacement by 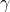 percent. The second replacement’s NPV increase by
percent. The second replacement’s NPV increase by 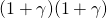 —over
the first one. Thus, the NPVs increased from NPV to
—over
the first one. Thus, the NPVs increased from NPV to 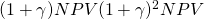 etc. We demonstrate the effect of technologically improved
replacement on the ranking of investments in Table 10.5. To
simplify our calculations, we assume that we have already found the
NPV of the two challengers equal to $100 for the first investment
and $150 for the second investment. The term differences of the two
investments are n1 = 10 for the
first investment and n2 = 20 for the second
investment. The rate of technological improvements are 5% for
investment one and 3% for investment two. To demonstrate the
importance of accounting for technological improvements, we find
the AE unadjusted for technological improvement and the AE
accounting for technological improvement.
etc. We demonstrate the effect of technologically improved
replacement on the ranking of investments in Table 10.5. To
simplify our calculations, we assume that we have already found the
NPV of the two challengers equal to $100 for the first investment
and $150 for the second investment. The term differences of the two
investments are n1 = 10 for the
first investment and n2 = 20 for the second
investment. The rate of technological improvements are 5% for
investment one and 3% for investment two. To demonstrate the
importance of accounting for technological improvements, we find
the AE unadjusted for technological improvement and the AE
accounting for technological improvement.
Table 10.6. Ranking Adjusted for Term Differences and Technologically Improved Replacements. Rankings Assuming Defender’s IRR is 10%
| Challenger |
NPV (rankings) |
Terms | Technological change
coefficient 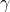 |
Adjustment coefficient
|
AE not adjusted for technological change (rankings) |
NPVs adjusted for technological change (rankings) |
| C1 |
NPV1 = $100 (2) |
n1 = 10 | 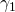 = 5%
= 5% |
1.68 |
$16.27 (2) |
$100(1.68) = $168 (1) |
| C2 |
NPV2 = $150 (2) |
n2 = 20 | 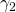 = 3%
= 3% |
1.18 |
$17.62 (1) |
$150(1.18) = $177.12 (2) |
It is useful to note in Table 10.6 that NPV and AE unadjusted for technological change are consistent as our theory implies. However, once we account for technological change, the investment rankings based on the investments AE are reversed. Investment one is preferred even though its NPV is less than that of challenger’s two NPV.
Inconsistent rankings were not caused by failing to adjust for differences in size and terms. As we have already demonstrated, these can be rationalized using AE. What produced the inconsistencies was comparing the rankings without technologically improved replacements (unadjusted AE) versus including the assumption of technologically improved replacements (adjusted for technology rankings).
Capitalizing AE to find the present value of a stream of repeatable investments. If we are comparing repeatable investments with different terms, then the comparisons are not between individual investments but with the present value sum of all the investments in each cash flow stream. In this regard we could compare the AE since the AE ordering of investment is the same as the NPV orderings. Or, we could capitalize the AE to find the present value sum of all of the investments. To understand how to capitalize the AE, that is, to find its value over an infinite number of repeatable investments, we write Equation \ref{10.26}:
(10.26)
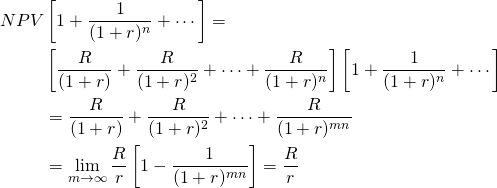
To get some idea of how fast convergent to the capitalization formula R/r occurs in Equation \ref{10.26}, if n = 10 and r = 10%, then for m = 2, then [1 – 1/(1 + r)mn] = .85; for m = 3, then [1 – 1/(1 + r)mn] = .94, and for m = 4, then [1 – 1/(1 + r)mn] = .98. Finally, for m = 5, then [1 – 1/(1 + r)mn] = .991.
Finding the Optimal Replacement Age for Different Repeatable Investments
The condition that identifies the optimal replacement age for a repeatable investment. The optimal age for each repeatable investment in a stream of repeatable investments is that age that maximizes the NPV for the entire stream of repeatable investments. Finding the optimal age of a repeatable investment is a ranking problem. Only in this case, each challenger is defined by its replacement age, and each age-differentiated investment is considered to be a different challenger. Our goal is to find optimal replacement age.
The key to understanding when to replace repeatable investments (without employing a lot of calculus) is to think about averages—or in our case, AE. We want to maximize the present value sum of NPVs for the entire stream of repeatable investments—not just the NPV for an individual investment.
If the investments in a series of repeatable investments have identical cash flow patterns, then the rule for maximizing the NPV of the present value sum for all repeatable investment is to find the term that maximizes the AE for a single investment. Thus, for a repeatable investment, if holding the investment for an additional period increases the AE for the challenger, then the investment should be held for at least another period—until holding the investment another period decreases the AE. Of course, the periodic cash flows could still be positive and NPV increasing even though AE are decreasing. Thus holding the investment for the term that maximizes its NPV is definitely not the same rule as holding the investment for the term that maximizes its AE.
The pattern of cash flows is the ultimate determinant of an investment’s optimal life. Since the calculus requires a smooth inverted cup-like shape for maximization, we typically assume investment cash flows have corresponding patterns. However, the pattern for an investment’s periodic cash flows are not the same as the pattern of AE for an investment at different ages. Consider some different kinds of investments and cash flow patterns and their corresponding optimal lives.
Finding the optimal replacement age for a growth and decay type investment. The growth and decay type of investment, after the initial investment, is identified by increasing periodic cash flows followed by decreasing periodic cash flows. Specifically, suppose that we have a repeatable investment with cash flows reported for 6 periods. Assuming the reinvestment rate and the discount rate are 10%, we find the NPV for each investment assuming it has an economic life of one period, two periods, three periods, and up to six periods. Then we find the AE for the investments at their alternative economic lives. Finally, we capitalized the AE by 10% (divide the AE by .1) to find the lifetime present value of the multiple investments at their alternative ages. The results are reported in Table 10.7.
Table 10.7. An Example of a Growth and Decay Type Investment.
| Time period | Cash flow per period | NPV per investment for alternative investment lives discounted at 10% | AE per investment for alternative investment lives discounted at 10% | Present value sum of an infinite number of repeatable investments |
| 0 | ($300.00) | ($300.00) | ||
| 1 | $150.00 | ($163.64) | ($180.00) | ($18,000.00) |
| 2 | $275.00 | $63.64 | $36.67 | $3,667.00 |
| 3 | $130.00 | $161.31 | $64.87 | $6,487.00 |
| 4 | $70.00 | $209.12 | $65.97 | $6,597.00 |
| 5 | $30.00 | $227.75 | $60.08 | $6,008.00 |
| 6 | ($10.00) | $222.10 | $51.00 | $5,100.00 |
If our goal were to maximize the NPV for one of the repeatable investments, we would hold the investment until it no longer produced positive cash flows—in our example until period 5 with a cash flow of $30 and lifetime present earnings of $6,008.00. But if our goal is to optimize our lifetime earnings from a large number of repeatable investments, then we would hold each investment until they reach age 4 with a cash flow of $70 and lifetime earnings of $6,597.00. Another way to report the results of Table 10.6 is to note that as long as the periodic cash flow exceeds the AE in a period, adding that period to the life of the investment will increase the AE and the lifetime earnings of the repeatable investments.
Finding the optimal replacement age for a light bulb type investment. Recall that the “light bulb” type of investment describes a category of investments which, after the initial investment, produce a nearly constant level of services that are virtually undiminished over its economic life. Then, at some point, the investment stops providing services and the investment dies a sudden death. An example cash flow pattern for this investment assumes that the investment dies in period 5. The investment is described in Table 10.8.
Table 10.8. An Example of a Light Bulb Type Investment.
| Time period | Cash flow per period | NPV per investment for alternative investment lives discounted at 10% | AE per investment for alternative investment lives discounted at 10% | Present value sum of an infinite number of repeatable investments |
| 0 | ($300.00) | ($300.00) | ||
| 1 | $100.00 | ($209.09) | ($230.00) | ($23,000.00) |
| 2 | $100.00 | ($126.45) | ($72.86) | ($7,286.00) |
| 3 | $100.00 | ($51.31) | ($20.63) | ($2,063.00) |
| 4 | $100.00 | $16.99 | $5.36 | $536.00 |
| 5 | $0 | $16.99 | $4.48 | $448.00 |
| 6 | $0 | $16.99 | $3.90 | $390.00 |
The light bulb type investment has an important pattern that is easily recognized. It is that as long as its constant cash flows are positive, it’s NPV and AE are increasing. However, once the investment dies and its positive cash flows end, its NPV is constant but its AE is continually decreasing. Thus, the optimal life of a light bulb is to keep it until it dies. Of course, this recommendation could be modified if there were serious costs associated with an interruption of services and that the exact period in which the investment died was not known with certainty.
Finding the optimal replacement age for a continuous decay type investment. The continuous decay type investment is one in which the investment performs best when new and then, with use and time, its service capacity decreases and its maintenance requirements increase so that its periodic cash flows exhibit a continuous decay. An example of such a periodic cash flow pattern is described in Table 10.9.
Table 10.9. An Example of the Continual Decay Type Investment.
| Time period | Cash flow per period | NPV per investment for alternative investment lives discounted at 10% | AE per investment for alternative investment lives discounted at 10% | Present value sum of an infinite number of repeatable investments |
| 0 | ($4300.00) | ($300.00) | ||
| 1 | $190.00 | ($127.27) | ($139.96) | ($13,996.00) |
| 2 | $152.00 | ($1.65) | ($.95) | ($95.00) |
| 3 | $129.00 | $95.27 | $38.31 | $3,831.00 |
| 4 | $85.00 | $153.32 | $48.37 | $4,837.00 |
| 5 | $38.00 | $175.92 | $46.41 | $4,641.00 |
| 6 | $8.00 | $181.43 | $41.66 | $4,166.00 |
In the continual decay model, after the cost of the initial investment is paid, the periodic cash flows of the investment continually decrease. Still they increase the NPV of the investment as long as they are positive. At some point, the value of earning high returns during the early life of the investment swamps the cost of acquiring a new investment and the AE decrease indicating the optimal age of the investment. In this example, the optimal life of the investment is 4 periods with a corresponding present value sum of earnings over an infinite number of repeatable investments equal to $4,837.00.
Finding the optimal replacement age for an investment with irregular periodic cash flows. The last category of investments considered are those whose cash flow patterns are unique. That is, the cash flow pattern for an investment owned one year is different than the same investment owned two years, three years, and so on. To illustrate this type of investment, consider a machinery owner who custom hires using his machine to perform services for customers. The cash flow pattern for the machine begins with a capital purchase followed by three years of nearly constant cash flows which then decrease by 25% per year—mostly because of repairs but also because the demand for custom hires using older machines decreases. In the year the machine is replaced, the old machine earns a liquidation value that depends on the age of the machine. In this problem, the machine at each age is considered a unique challenger even though it is the same machine differentiated by age. A description of the cash flows for this problem follows.
Table 10.10 Investments With Irregular Cash Flow Characterized by Constant and then Declining Cash Flow with an Income Spike in the last Period of the Investment’s Economic Life. The Discount and Reinvestment Rates are Assumed to Equal 10%.
| Period | 3 year old challenger | 4 year old challenger | 5 year old challenger | 6 year old challenger | 7 year old challenger | 8 year old challenger |
| 0 | ($100) | ($100) | ($100) | ($100) | ($100) | ($100) |
| 1 | $40 | $40 | $40 | $40 | $40 | $40 |
| 2 | $40 | $40 | $40 | $40 | $40 | $40 |
| 3 | liquidation = $64 | $32 | $32 | $32 | $32 | $32 |
| 4 | 0 | liquidation = $51.20 | $25.60 | $25.60 | $25.60 | $25.60 |
| 5 | 0 | 0 | liquidation = $40.96 | $20.48 | $20.48 | $20.48 |
| 6 | 0 | 0 | 0 | liquidation = $32.77 | 16.38 | $16.38 |
| 7 | 0 | 0 | 0 | 0 | liquidation = $26.21 | $13.11 |
| 8 | 0 | 0 | 0 | 0 | 0 | liquidation = $20.97 |
| Summary Measures | ||||||
| NPVs | $17.51 | $28.43 | $36.38 | $42.16 | $46.36 | $49.42 |
| AE | $7.04 | $8.97 | $9.60 | $9.68 | $9.52 | $9.26 |
| Capitalized AE | $70.40 | $89.70 | $96.00 | $96.80 | $95.20 | $92.60 |
Note that NPVs are increasing with the age of the challengers. The maximum AE is earned in the sixth period and declines for each of the older challengers. Thus the optimal age for the challengers is age 6.
Summary and Conclusions
In Chapter 9, we found two sufficient conditions for consistently ranking mutually exclusive investments. The two conditions are that initial investment sizes and periodic cash flows are equal except for their last common period. In this chapter we extended the results of Chapter 9 by developing methods to rank investments of unequal terms. Ranking unequal term investments are problematic because unequal terms create unequal periodic cash flows, violating the second of two sufficient conditions for consistently ranking investments using IRRs and NPVs.
In our efforts to find methods for ranking investments of unequal terms, we found that MNPV and MIRR models would rank investments equally. But we also found that under some conditions, IRR and NPV models could produce equal rankings. In this chapter, we emphasized that adjusting for term differences by reinvesting and discounting by the defender’s IRR that NPV and MNPV and MIRR models would produce consistent rankings. These results would not hold when some other reinvestment rate applies. These findings led to some important practical results: when the reinvestment rate and the discount rate are the same, rank investments using NPVs. When the reinvestment rates are the investments’ IRRs, rank using investments’ IRRs.
In the second part of this chapter, we considered repeatable investments. If by repeating investments for a required number of times the investments had a common ending date, then individual investment term differences could be ignored. In effect, the entire stream of repeatable investments could be considered to be a single investment. Of course, if the number of repeatable investments was considered to be infinite then the term problem is resolved.
Assuming equal initial investment sizes, we found that the repeatable investment’s optimal age was the age that maximized AE for a single investment. Thus, we can find the optimal replacement age for repeatable investments in a stream of replacements by finding the age that maximizes AE for any one investment. Capitalizing the AE provides us with an estimate of the present value of the earnings from the stream of repeatable investments.
Questions
- Describe the three sufficient conditions required for consistent IRR and NPV rankings for one-time investments? Explain how investment term differences violate one of the two sufficient conditions.
- Some investments are one-time investments. Others are repeatable. Describe what conditions produce one-time investments. Then describe what conditions produce repeatable investments. Give examples of one-time and repeatable investments.
- One way to resolve term differences is to reinvest the periodic cash flows of both investments to a common ending period. Explain the implications of assuming that the reinvestment rates are the defender’s IRR, the investments’ IRR, or some other rate.
- Explain the effects on an investment’s NPV if term differences are resolved by reinvesting its periodic cash flows to some common period using the defender’s IRR, while discounting the reinvested funds over the changed terms by the same rate, the defender’s IRR.
- Explain the difference, if any, between an investment’s IRR and its MIRR if the reinvestment rate is the investment’s IRR. Depending on your answer, what practical recommendation would you offer to financial managers wanting to rank investments whose earnings would be reinvested in themselves?
- In the table below, term differences are resolved by reinvesting periodic cash flows to the common ending period assuming the reinvestment rate and the discount rate is the defender’s IRR of 10%. Produce a similar table assuming the same initial investment sizes and cash flows, only assume the defender’s IRR is 5% not 10%. Then associate your results with the ranking possibilities described in Table 10.1 by declaring which of the four models correspond to your table.
Table Q10.1. The influence of periodic size and term differences created by differential withdrawals assuming a reinvestment rate equal to the defender’s IRR of 10%. The discount rate for the NPV and MNPV models equal the defender’s IRR. The discount rate for the IRR and MIRR models are the IRRs and MIRRs
| Challengers | Initial Outlay | Cash Flow in period one | Cash Flow in period two |
NPV (rankings) |
IRR (rankings) |
MNPV (rankings) |
MIRR (rankings) |
| C1 | $900 | $1090 | 0 | $90.91 (2) |
$21.11% (1) |
$90.91 (2) |
15.42% (2) |
| C2 | $900 | $160 | $1050 | $113.22 (1) |
17.27% (2) |
$113.22 (1) |
16.71% (1) |
- In the table below, term differences are resolved by reinvesting periodic cash flows to the common ending period assuming the reinvestment rates are the investments’ IRRs and the discount rate is 10%. Produce a similar table assuming the same initial investment sizes and cash flows, only assume the defender’s IRR is 5% not 10%. Then associate your results with the ranking possibilities described in Table 10.1 by declaring which of the four models correspond to your table.
Table Q10.2.The influence of periodic size and term differences created by differential withdrawals assuming a reinvestment rate equal to the challenger’s IRRs. The discount rate for the NPV and MNPV models equal the defender’s IRR. The discount rate for the IRR and MIRR models are the IRRs and MIRRs.
| Challengers | Initial Outlay | Cash Flow in period one | Cash Flow in period two |
NPV (rankings) |
IRR (rankings) |
MNPV (rankings) |
MIRR (rankings) |
| C1 | $900 | $1090 | $0 | $90.91 (2) |
$21.11% (1) |
$190.91 (1) |
21.11% (1) |
| C2 | $900 | $160 | $1050 | $113.22 (1) |
17.27% (2) |
$122.83 (2) |
17.27% (2) |
- Referring to the completed tables in Questions 6 and 7, please answer the following. Why are NPV and MNPV ranking consistent and equal in amounts in the Question 6 table but inconsistent and different in amounts in the Question 7 table? And why are IRR and MIRR rankings inconsistent and unequal in the Question 6 table but consistent and equal in amount in the Question 7 table? What are the practical implications of these results?
- Annuity equivalents are elements in a stream of constant periodic cash flows whose present value equals the present value of some fixed amount or the present value of a non-constant cash flow stream. What is the arithmetic mean of a series of AE? If the discount rate is 8% and the term is 10 periods, find the AE for the periodic cash flows 21, 34, 5, and 13. Then find the AE for a fixed present value amount of $199 assuming the same discount rate and term. Finally, recalculate the AE if the term is decreased from 10 periods to 5 periods.
- A potential Uber driver can purchase a new car for $18,000. Then the car is expected to earn constant periodic cash flows for the next three years of $6,000. After that, mostly because of decreased demand for rides in older cars and higher repair costs, periodic cash flows decrease by 25% per year. The liquidation value of the new car after three years is $9,000 and then declines each year thereafter by 25%. Find the optimal age at which the Uber driver should replace cars. Then find the capitalized value of an investment in one car assuming each car is owned until its optimal age.